Boosting as a kernel-based method
Paper and Code
Apr 13, 2017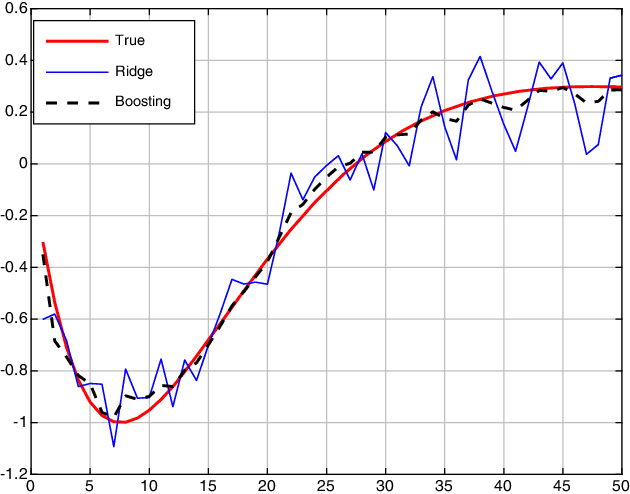

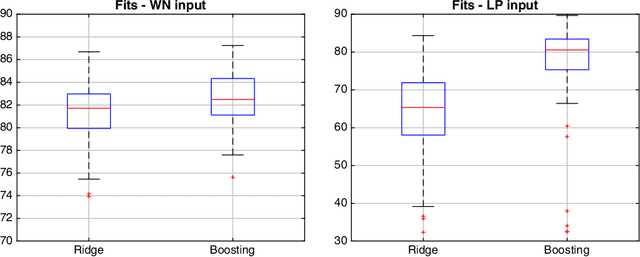
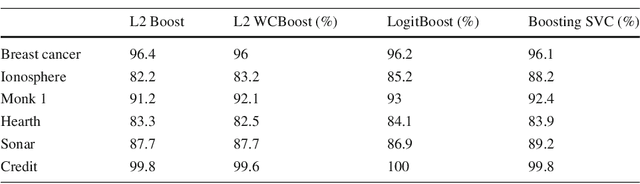
Boosting combines weak (biased) learners to obtain effective learning algorithms for classification and prediction. In this paper, we show a connection between boosting and kernel-based methods, highlighting both theoretical and practical applications. In the context of $\ell_2$ boosting, we start with a weak linear learner defined by a kernel $K$. We show that boosting with this learner is equivalent to estimation with a special {\it boosting kernel} that depends on $K$, as well as on the regression matrix, noise variance, and hyperparameters. The number of boosting iterations is modeled as a continuous hyperparameter, and fit along with other parameters using standard techniques. We then generalize the boosting kernel to a broad new class of boosting approaches for more general weak learners, including those based on the $\ell_1$, hinge and Vapnik losses. The approach allows fast hyperparameter tuning for this general class, and has a wide range of applications, including robust regression and classification. We illustrate some of these applications with numerical examples on synthetic and real data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge