DeepBayes -- an estimator for parameter estimation in stochastic nonlinear dynamical models
Paper and Code
May 04, 2022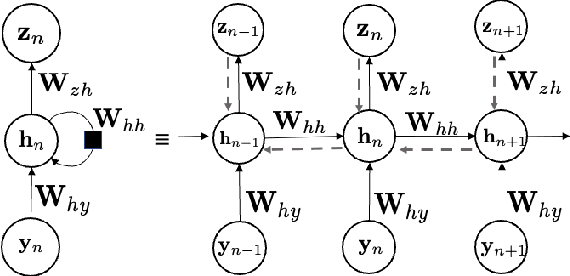
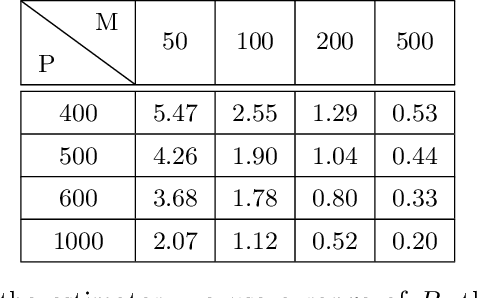

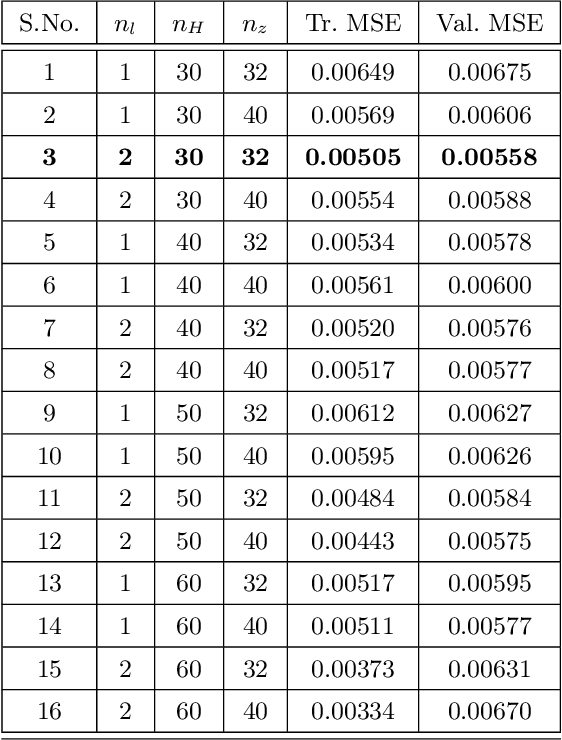
Stochastic nonlinear dynamical systems are ubiquitous in modern, real-world applications. Yet, estimating the unknown parameters of stochastic, nonlinear dynamical models remains a challenging problem. The majority of existing methods employ maximum likelihood or Bayesian estimation. However, these methods suffer from some limitations, most notably the substantial computational time for inference coupled with limited flexibility in application. In this work, we propose DeepBayes estimators that leverage the power of deep recurrent neural networks in learning an estimator. The method consists of first training a recurrent neural network to minimize the mean-squared estimation error over a set of synthetically generated data using models drawn from the model set of interest. The a priori trained estimator can then be used directly for inference by evaluating the network with the estimation data. The deep recurrent neural network architectures can be trained offline and ensure significant time savings during inference. We experiment with two popular recurrent neural networks -- long short term memory network (LSTM) and gated recurrent unit (GRU). We demonstrate the applicability of our proposed method on different example models and perform detailed comparisons with state-of-the-art approaches. We also provide a study on a real-world nonlinear benchmark problem. The experimental evaluations show that the proposed approach is asymptotically as good as the Bayes estimator.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge