Improved Sample Complexity of Imitation Learning for Barrier Model Predictive Control

Recent work in imitation learning has shown that having an expert controller that is both suitably smooth and stable enables stronger guarantees on the performance of the learned controller. However, constructing such smoothed expert controllers for arbitrary systems remains challenging, especially in the presence of input and state constraints. As our primary contribution, we show how such a smoothed expert can be designed for a general class of systems using a log-barrier-based relaxation of a standard Model Predictive Control (MPC) optimization problem. Improving upon our previous work, we show that barrier MPC achieves theoretically optimal error-to-smoothness tradeoff along some direction. At the core of this theoretical guarantee on smoothness is an improved lower bound we prove on the optimality gap of the analytic center associated with a convex Lipschitz function, which we believe could be of independent interest. We validate our theoretical findings via experiments, demonstrating the merits of our smoothing approach over randomized smoothing.

Imitating Complex Trajectories: Bridging Low-Level Stability and High-Level Behavior

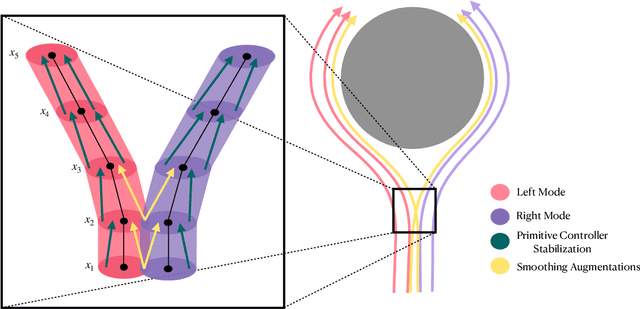
We propose a theoretical framework for studying the imitation of stochastic, non-Markovian, potentially multi-modal (i.e. "complex" ) expert demonstrations in nonlinear dynamical systems. Our framework invokes low-level controllers - either learned or implicit in position-command control - to stabilize imitation policies around expert demonstrations. We show that with (a) a suitable low-level stability guarantee and (b) a stochastic continuity property of the learned policy we call "total variation continuity" (TVC), an imitator that accurately estimates actions on the demonstrator's state distribution closely matches the demonstrator's distribution over entire trajectories. We then show that TVC can be ensured with minimal degradation of accuracy by combining a popular data-augmentation regimen with a novel algorithmic trick: adding augmentation noise at execution time. We instantiate our guarantees for policies parameterized by diffusion models and prove that if the learner accurately estimates the score of the (noise-augmented) expert policy, then the distribution of imitator trajectories is close to the demonstrator distribution in a natural optimal transport distance. Our analysis constructs intricate couplings between noise-augmented trajectories, a technique that may be of independent interest. We conclude by empirically validating our algorithmic recommendations.

Smooth Model Predictive Control with Applications to Statistical Learning

Statistical learning theory and high dimensional statistics have had a tremendous impact on Machine Learning theory and have impacted a variety of domains including systems and control theory. Over the past few years we have witnessed a variety of applications of such theoretical tools to help answer questions such as: how many state-action pairs are needed to learn a static control policy to a given accuracy? Recent results have shown that continuously differentiable and stabilizing control policies can be well-approximated using neural networks with hard guarantees on performance, yet often even the simplest constrained control problems are not smooth. To address this void, in this paper we study smooth approximations of linear Model Predictive Control (MPC) policies, in which hard constraints are replaced by barrier functions, a.k.a. barrier MPC. In particular, we show that barrier MPC inherits the exponential stability properties of the original non-smooth MPC policy. Using a careful analysis of the proposed barrier MPC, we show that its smoothness constant can be carefully controlled, thereby paving the way for new sample complexity results for approximating MPC policies from sampled state-action pairs.

The Power of Learned Locally Linear Models for Nonlinear Policy Optimization

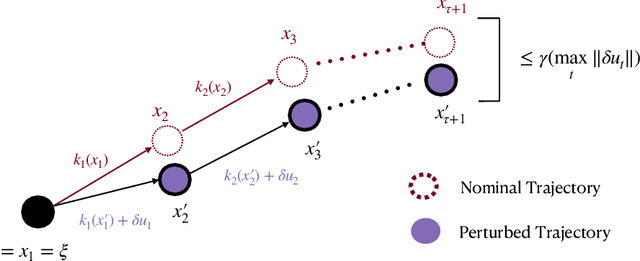
A common pipeline in learning-based control is to iteratively estimate a model of system dynamics, and apply a trajectory optimization algorithm - e.g.~$\mathtt{iLQR}$ - on the learned model to minimize a target cost. This paper conducts a rigorous analysis of a simplified variant of this strategy for general nonlinear systems. We analyze an algorithm which iterates between estimating local linear models of nonlinear system dynamics and performing $\mathtt{iLQR}$-like policy updates. We demonstrate that this algorithm attains sample complexity polynomial in relevant problem parameters, and, by synthesizing locally stabilizing gains, overcomes exponential dependence in problem horizon. Experimental results validate the performance of our algorithm, and compare to natural deep-learning baselines.

TaSIL: Taylor Series Imitation Learning

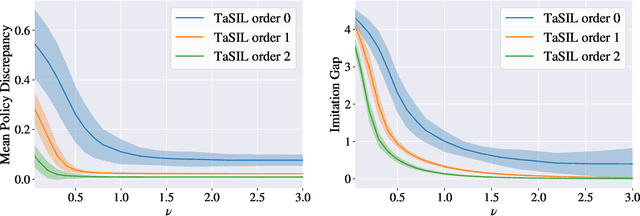
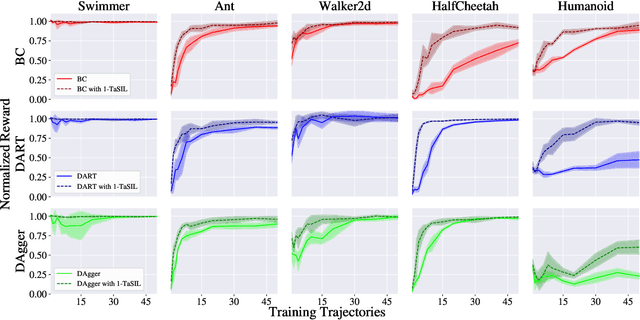
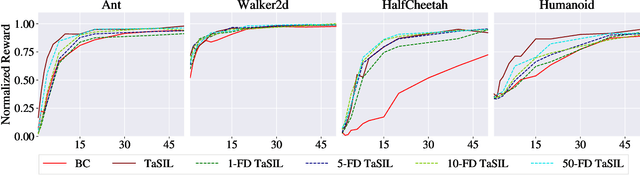
We propose Taylor Series Imitation Learning (TaSIL), a simple augmentation to standard behavior cloning losses in the context of continuous control. TaSIL penalizes deviations in the higher-order Taylor series terms between the learned and expert policies. We show that experts satisfying a notion of \emph{incremental input-to-state stability} are easy to learn, in the sense that a small TaSIL-augmented imitation loss over expert trajectories guarantees a small imitation loss over trajectories generated by the learned policy. We provide sample-complexity bounds for TaSIL that scale as $\tilde{\mathcal{O}}(1/n)$ in the realizable setting, for $n$ the number of expert demonstrations. Finally, we demonstrate experimentally the relationship between the robustness of the expert policy and the order of Taylor expansion required in TaSIL, and compare standard Behavior Cloning, DART, and DAgger with TaSIL-loss-augmented variants. In all cases, we show significant improvement over baselines across a variety of MuJoCo tasks.

Linear Variational State Space Filtering

We introduce Variational State-Space Filters (VSSF), a new method for unsupervised learning, identification, and filtering of latent Markov state space models from raw pixels. We present a theoretically sound framework for latent state space inference under heterogeneous sensor configurations. The resulting model can integrate an arbitrary subset of the sensor measurements used during training, enabling the learning of semi-supervised state representations, thus enforcing that certain components of the learned latent state space to agree with interpretable measurements. From this framework we derive L-VSSF, an explicit instantiation of this model with linear latent dynamics and Gaussian distribution parameterizations. We experimentally demonstrate L-VSSF's ability to filter in latent space beyond the sequence length of the training dataset across several different test environments.

UNIFY: Multi-Belief Bayesian Grid Framework based on Automotive Radar

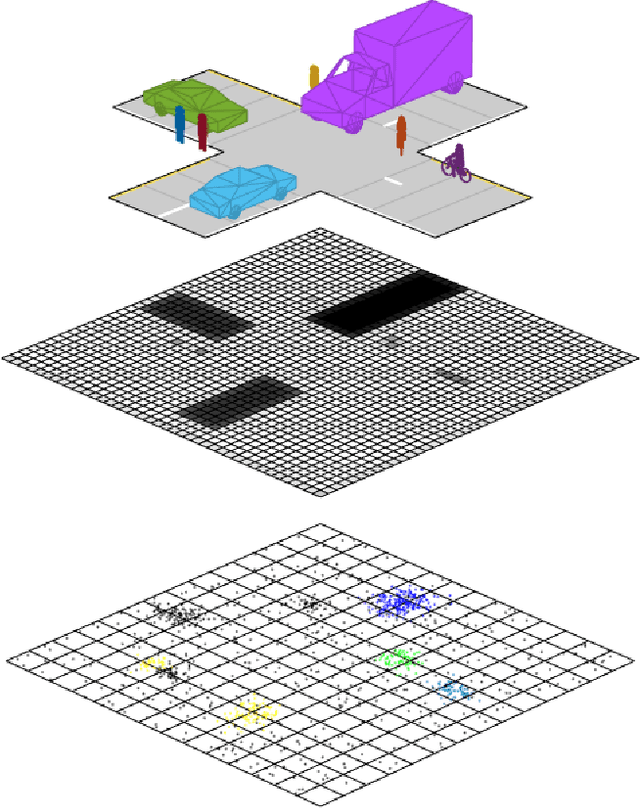
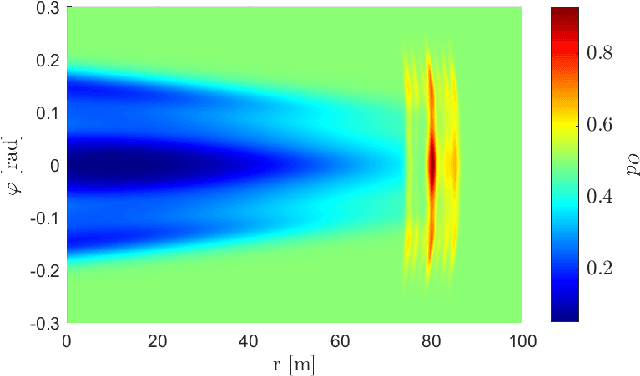
Grid maps are widely established for the representation of static objects in robotics and automotive applications. Though, incorporating velocity information is still widely examined because of the increased complexity of dynamic grids concerning both velocity measurement models for radar sensors and the representation of velocity in a grid framework. In this paper, both issues are addressed: sensor models and an efficient grid framework, which are required to ensure efficient and robust environment perception with radar. To that, we introduce new inverse radar sensor models covering radar sensor artifacts such as measurement ambiguities to integrate automotive radar sensors for improved velocity estimation. Furthermore, we introduce UNIFY, a multiple belief Bayesian grid map framework for static occupancy and velocity estimation with independent layers. The proposed UNIFY framework utilizes a grid-cell-based layer to provide occupancy information and a particle-based velocity layer for motion state estimation in an autonomous vehicle's environment. Each UNIFY layer allows individual execution as well as simultaneous execution of both layers for optimal adaption to varying environments in autonomous driving applications. UNIFY was tested and evaluated in terms of plausibility and efficiency on a large real-world radar data-set in challenging traffic scenarios covering different densities in urban and rural sceneries.