Meta-Learning Operators to Optimality from Multi-Task Non-IID Data

A powerful concept behind much of the recent progress in machine learning is the extraction of common features across data from heterogeneous sources or tasks. Intuitively, using all of one's data to learn a common representation function benefits both computational effort and statistical generalization by leaving a smaller number of parameters to fine-tune on a given task. Toward theoretically grounding these merits, we propose a general setting of recovering linear operators $M$ from noisy vector measurements $y = Mx + w$, where the covariates $x$ may be both non-i.i.d. and non-isotropic. We demonstrate that existing isotropy-agnostic meta-learning approaches incur biases on the representation update, which causes the scaling of the noise terms to lose favorable dependence on the number of source tasks. This in turn can cause the sample complexity of representation learning to be bottlenecked by the single-task data size. We introduce an adaptation, $\texttt{De-bias & Feature-Whiten}$ ($\texttt{DFW}$), of the popular alternating minimization-descent (AMD) scheme proposed in Collins et al., (2021), and establish linear convergence to the optimal representation with noise level scaling down with the $\textit{total}$ source data size. This leads to generalization bounds on the same order as an oracle empirical risk minimizer. We verify the vital importance of $\texttt{DFW}$ on various numerical simulations. In particular, we show that vanilla alternating-minimization descent fails catastrophically even for iid, but mildly non-isotropic data. Our analysis unifies and generalizes prior work, and provides a flexible framework for a wider range of applications, such as in controls and dynamical systems.

TaSIL: Taylor Series Imitation Learning

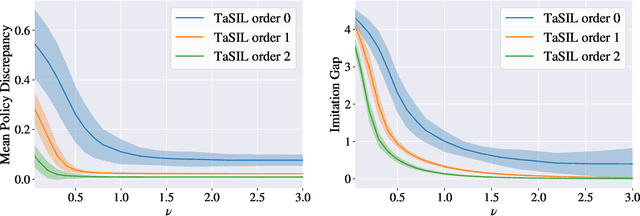
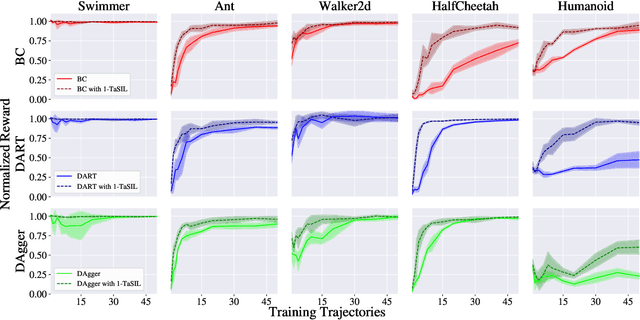
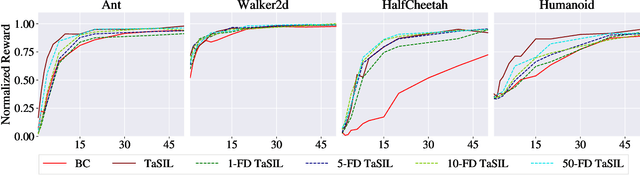
We propose Taylor Series Imitation Learning (TaSIL), a simple augmentation to standard behavior cloning losses in the context of continuous control. TaSIL penalizes deviations in the higher-order Taylor series terms between the learned and expert policies. We show that experts satisfying a notion of \emph{incremental input-to-state stability} are easy to learn, in the sense that a small TaSIL-augmented imitation loss over expert trajectories guarantees a small imitation loss over trajectories generated by the learned policy. We provide sample-complexity bounds for TaSIL that scale as $\tilde{\mathcal{O}}(1/n)$ in the realizable setting, for $n$ the number of expert demonstrations. Finally, we demonstrate experimentally the relationship between the robustness of the expert policy and the order of Taylor expansion required in TaSIL, and compare standard Behavior Cloning, DART, and DAgger with TaSIL-loss-augmented variants. In all cases, we show significant improvement over baselines across a variety of MuJoCo tasks.

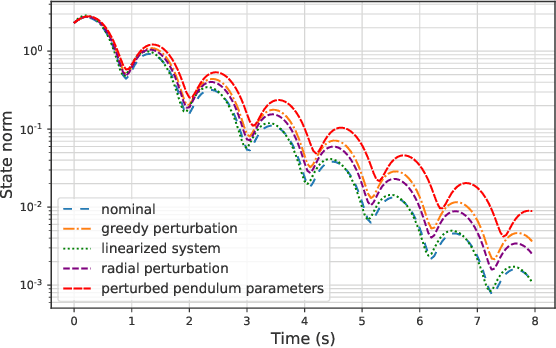
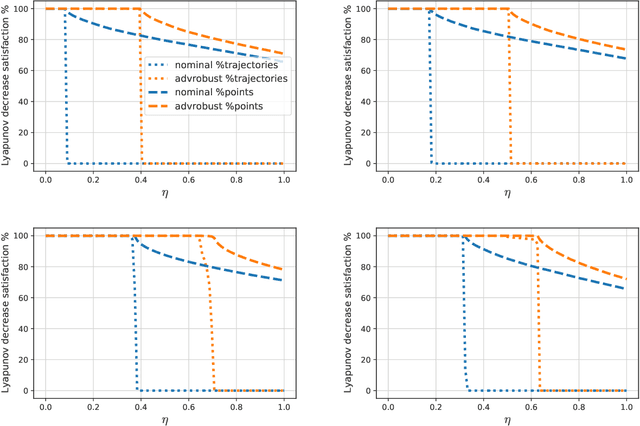
Adversarially Robust Stability Certificates can be Sample-Efficient

Motivated by bridging the simulation to reality gap in the context of safety-critical systems, we consider learning adversarially robust stability certificates for unknown nonlinear dynamical systems. In line with approaches from robust control, we consider additive and Lipschitz bounded adversaries that perturb the system dynamics. We show that under suitable assumptions of incremental stability on the underlying system, the statistical cost of learning an adversarial stability certificate is equivalent, up to constant factors, to that of learning a nominal stability certificate. Our results hinge on novel bounds for the Rademacher complexity of the resulting adversarial loss class, which may be of independent interest. To the best of our knowledge, this is the first characterization of sample-complexity bounds when performing adversarial learning over data generated by a dynamical system. We further provide a practical algorithm for approximating the adversarial training algorithm, and validate our findings on a damped pendulum example.