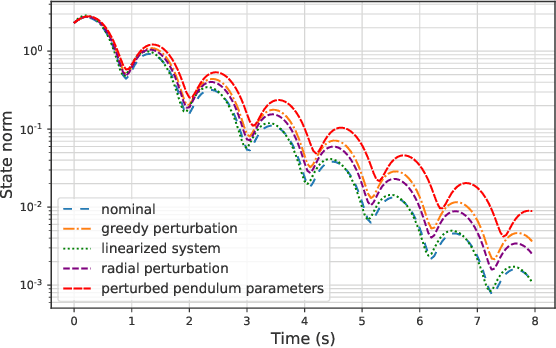
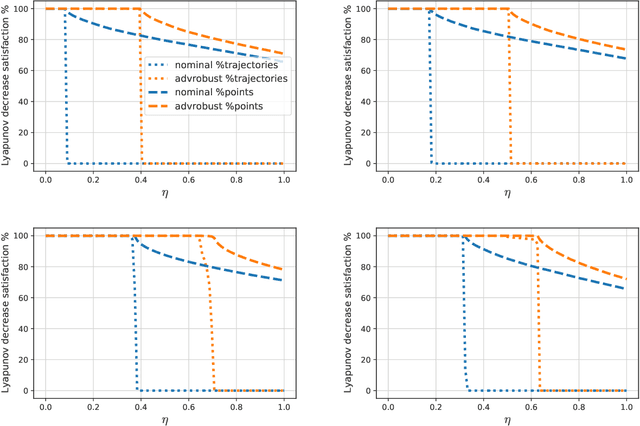
Adversarially Robust Stability Certificates can be Sample-Efficient

Motivated by bridging the simulation to reality gap in the context of safety-critical systems, we consider learning adversarially robust stability certificates for unknown nonlinear dynamical systems. In line with approaches from robust control, we consider additive and Lipschitz bounded adversaries that perturb the system dynamics. We show that under suitable assumptions of incremental stability on the underlying system, the statistical cost of learning an adversarial stability certificate is equivalent, up to constant factors, to that of learning a nominal stability certificate. Our results hinge on novel bounds for the Rademacher complexity of the resulting adversarial loss class, which may be of independent interest. To the best of our knowledge, this is the first characterization of sample-complexity bounds when performing adversarial learning over data generated by a dynamical system. We further provide a practical algorithm for approximating the adversarial training algorithm, and validate our findings on a damped pendulum example.

Random features for adaptive nonlinear control and prediction

A key assumption in the theory of adaptive control for nonlinear systems is that the uncertainty of the system can be expressed in the linear span of a set of known basis functions. While this assumption leads to efficient algorithms, verifying it in practice can be difficult, particularly for complex systems. Here we leverage connections between reproducing kernel Hilbert spaces, random Fourier features, and universal approximation theory to propose a computationally tractable algorithm for both adaptive control and adaptive prediction that does not rely on a linearly parameterized unknown. Specifically, we approximate the unknown dynamics with a finite expansion in $\textit{random}$ basis functions, and provide an explicit guarantee on the number of random features needed to track a desired trajectory with high probability. Remarkably, our explicit bounds only depend $\textit{polynomially}$ on the underlying parameters of the system, allowing our proposed algorithms to efficiently scale to high-dimensional systems. We study a setting where the unknown dynamics splits into a component that can be modeled through available physical knowledge of the system and a component that lives in a reproducing kernel Hilbert space. Our algorithms simultaneously adapt over parameters for physical basis functions and random features to learn both components of the dynamics online.

Adaptive Variants of Optimal Feedback Policies

We combine adaptive control directly with optimal or near-optimal value functions to enhance stability and closed-loop performance in systems with parametric uncertainties. Leveraging the fundamental result that a value function is also a control Lyapunov function (CLF), combined with the fact that direct adaptive control can be immediately used once a CLF is known, we prove asymptotic closed-loop convergence of adaptive feedback controllers derived from optimization-based policies. Both matched and unmatched parametric variations are addressed, where the latter exploits a new technique based on adaptation rate scaling. The results may have particular resonance in machine learning for dynamical systems, where nominal feedback controllers are typically optimization-based but need to remain effective (beyond mere robustness) in the presence of significant but structured variations in parameters.

Adaptive-Control-Oriented Meta-Learning for Nonlinear Systems

Real-time adaptation is imperative to the control of robots operating in complex, dynamic environments. Adaptive control laws can endow even nonlinear systems with good trajectory tracking performance, provided that any uncertain dynamics terms are linearly parameterizable with known nonlinear features. However, it is often difficult to specify such features a priori, such as for aerodynamic disturbances on rotorcraft or interaction forces between a manipulator arm and various objects. In this paper, we turn to data-driven modeling with neural networks to learn, offline from past data, an adaptive controller with an internal parametric model of these nonlinear features. Our key insight is that we can better prepare the controller for deployment with control-oriented meta-learning of features in closed-loop simulation, rather than regression-oriented meta-learning of features to fit input-output data. Specifically, we meta-learn the adaptive controller with closed-loop tracking simulation as the base-learner and the average tracking error as the meta-objective. With a nonlinear planar rotorcraft subject to wind, we demonstrate that our adaptive controller outperforms other controllers trained with regression-oriented meta-learning when deployed in closed-loop for trajectory tracking control.

Universal Adaptive Control for Uncertain Nonlinear Systems

Precise motion planning and control require accurate models which are often difficult, expensive, or time-consuming to obtain. Online model learning is an attractive approach that can handle model variations while achieving the desired level of performance. However, several model learning methods developed within adaptive nonlinear control are limited to certain systems or types of uncertainties. In particular, the so-called unmatched uncertainties pose significant problems for existing methods if the system is not in a particular form. This work presents an adaptive control framework for nonlinear systems with unmatched uncertainties that addresses several of the limitations of existing methods through two key innovations. The first is leveraging contraction theory and a new type of contraction metric that, when coupled with an adaptation law, is able to track feasible trajectories generated by an adapting reference model. The second is a natural modulation of the learning rate so the closed-loop system remains stable during learning transients. The proposed approach is more general than existing methods as it is able to handle unmatched uncertainties while only requiring the system be nominally contracting in closed-loop. Additionally, it can be used with learned feedback policies that are known to be contracting in some metric, facilitating transfer learning and bridging the sim2real gap. Simulation results demonstrate the effectiveness of the method.

Regret Bounds for Adaptive Nonlinear Control

We study the problem of adaptively controlling a known discrete-time nonlinear system subject to unmodeled disturbances. We prove the first finite-time regret bounds for adaptive nonlinear control with matched uncertainty in the stochastic setting, showing that the regret suffered by certainty equivalence adaptive control, compared to an oracle controller with perfect knowledge of the unmodeled disturbances, is upper bounded by $\widetilde{O}(\sqrt{T})$ in expectation. Furthermore, we show that when the input is subject to a $k$ timestep delay, the regret degrades to $\widetilde{O}(k \sqrt{T})$. Our analysis draws connections between classical stability notions in nonlinear control theory (Lyapunov stability and contraction theory) and modern regret analysis from online convex optimization. The use of stability theory allows us to analyze the challenging infinite-horizon single trajectory setting.

Sliding on Manifolds: Geometric Attitude Control with Quaternions

This work proposes a quaternion-based sliding variable that describes exponentially convergent error dynamics for any forward complete desired attitude trajectory. The proposed sliding variable directly operates on the non-Euclidean space formed by quaternions and explicitly handles the double covering property to enable global attitude tracking when used in feedback. In-depth analysis of the sliding variable is provided and compared to others in the literature. Several feedback controllers including nonlinear PD, robust, and adaptive sliding control are then derived. Simulation results of a rigid body with uncertain dynamics demonstrate the effectiveness and superiority of the approach.

Neural Stochastic Contraction Metrics for Robust Control and Estimation

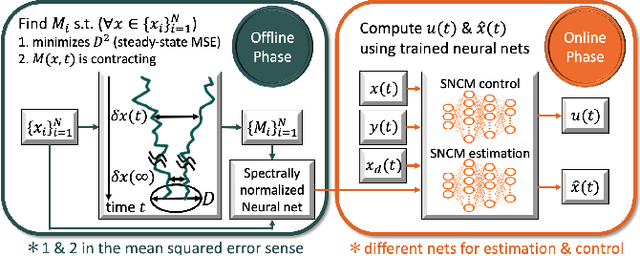
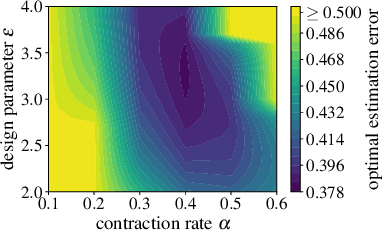
We present neural stochastic contraction metrics, a new design framework for provably-stable robust control and estimation for a class of stochastic nonlinear systems. It exploits a spectrally-normalized deep neural network to construct a contraction metric, sampled via simplified convex optimization in the stochastic setting. Spectral normalization constrains the state-derivatives of the metric to be Lipschitz continuous, and thereby ensures exponential boundedness of the mean squared distance of system trajectories under stochastic disturbances. This framework allows autonomous agents to approximate optimal stable control and estimation policies in real-time, and outperforms existing nonlinear control and estimation techniques including the state-dependent Riccati equation, iterative LQR, EKF, and deterministic neural contraction metric method, as illustrated in simulations.

Learning Stability Certificates from Data

Many existing tools in nonlinear control theory for establishing stability or safety of a dynamical system can be distilled to the construction of a certificate function that guarantees a desired property. However, algorithms for synthesizing certificate functions typically require a closed-form analytical expression of the underlying dynamics, which rules out their use on many modern robotic platforms. To circumvent this issue, we develop algorithms for learning certificate functions only from trajectory data. We establish bounds on the generalization error - the probability that a certificate will not certify a new, unseen trajectory - when learning from trajectories, and we convert such generalization error bounds into global stability guarantees. We demonstrate empirically that certificates for complex dynamics can be efficiently learned, and that the learned certificates can be used for downstream tasks such as adaptive control.

The Reflectron: Exploiting geometry for learning generalized linear models

Generalized linear models (GLMs) extend linear regression by generating the dependent variables through a nonlinear function of a predictor in a Reproducing Kernel Hilbert Space. Despite nonconvexity of the underlying optimization problem, the GLM-tron algorithm of Kakade et al. (2011) provably learns GLMs with guarantees of computational and statistical efficiency. We present an extension of the GLM-tron to a mirror descent or natural gradient-like setting, which we call the Reflectron. The Reflectron enjoys the same statistical guarantees as the GLM-tron for any choice of the convex potential function $\psi$ used to define mirror descent. Central to our algorithm, $\psi$ can be chosen to implicitly regularize the learned model when there are multiple hypotheses consistent with the data. Our results extend to the case of multiple outputs with or without weight sharing. We perform our analysis in continuous-time, leading to simple and intuitive derivations, with discrete-time implementations obtained by discretization of the continuous-time dynamics. We supplement our theoretical analysis with simulations on real and synthetic datasets demonstrating the validity of our theoretical results.