Information-Optimal Multi-Spacecraft Positioning for Interstellar Object Exploration

Interstellar objects (ISOs), astronomical objects not gravitationally bound to the sun, could present valuable opportunities to advance our understanding of the universe's formation and composition. In response to the unpredictable nature of their discoveries that inherently come with large and rapidly changing uncertainty in their state, this paper proposes a novel multi-spacecraft framework for locally maximizing information to be gained through ISO encounters with formal probabilistic guarantees. Given some approximated control and estimation policies for fully autonomous spacecraft operations, we first construct an ellipsoid around its terminal position, where the ISO would be located with a finite probability. The large state uncertainty of the ISO is formally handled here through the hierarchical property in stochastically contracting nonlinear systems. We then propose a method to find the terminal positions of the multiple spacecraft optimally distributed around the ellipsoid, which locally maximizes the information we can get from all the points of interest (POIs). This utilizes a probabilistic information cost function that accounts for spacecraft positions, camera specifications, and ISO position uncertainty, where the information is defined as visual data collected by cameras. Numerical simulations demonstrate the efficacy of this approach using synthetic ISO candidates generated from quasi-realistic empirical populations. Our method allows each spacecraft to optimally select its terminal state and determine the ideal number of POIs to investigate, potentially enhancing the ability to study these rare and fleeting interstellar visitors while minimizing resource utilization.

CART: Collision Avoidance and Robust Tracking Augmentation in Learning-based Motion Planning for Multi-Agent Systems

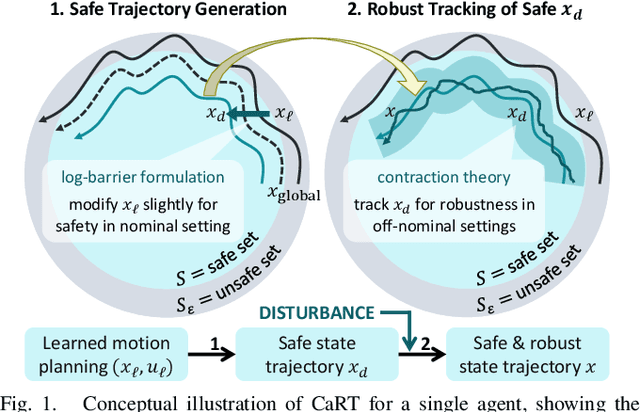
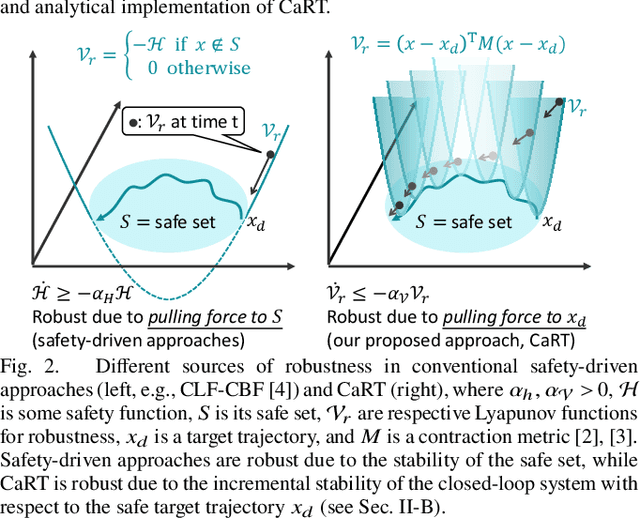
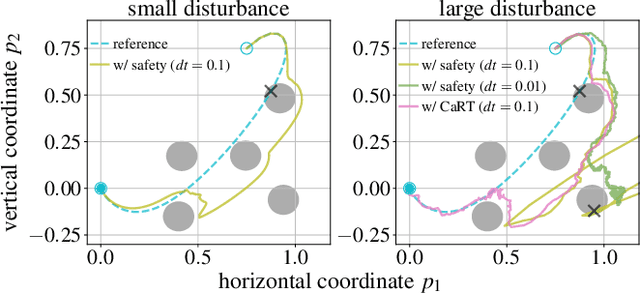
This paper presents CART, an analytical method to augment a learning-based, distributed motion planning policy of a nonlinear multi-agent system with real-time collision avoidance and robust tracking guarantees, independently of learning errors. We first derive an analytical form of an optimal safety filter for Lagrangian systems, which formally ensures a collision-free operation in a multi-agent setting in a disturbance-free environment, while allowing for its distributed implementation with minimal deviation from the learned policy. We then propose an analytical form of an optimal robust filter for Lagrangian systems to be used hierarchically with the learned collision-free target trajectory, which also enables distributed implementation and guarantees exponential boundedness of the trajectory tracking error for safety, even under the presence of deterministic and stochastic disturbance. These results are shown to extend further to general control-affine nonlinear systems using contraction theory. Our key contribution is to enhance the performance of the learned motion planning policy with collision avoidance and tracking-based robustness guarantees, independently of its original performance such as approximation errors and regret bounds in machine learning. We demonstrate the effectiveness of CART in motion planning and control of several examples of nonlinear systems, including spacecraft formation flying and rotor-failed UAV swarms.

Interstellar Object Accessibility and Mission Design

Interstellar objects (ISOs) are fascinating and under-explored celestial objects, providing physical laboratories to understand the formation of our solar system and probe the composition and properties of material formed in exoplanetary systems. This paper will discuss the accessibility of and mission design to ISOs with varying characteristics, including a discussion of state covariance estimation over the course of a cruise, handoffs from traditional navigation approaches to novel autonomous navigation for fast flyby regimes, and overall recommendations about preparing for the future in situ exploration of these targets. The lessons learned also apply to the fast flyby of other small bodies including long-period comets and potentially hazardous asteroids, which also require a tactical response with similar characteristics

Neural-Rendezvous: Learning-based Robust Guidance and Control to Encounter Interstellar Objects

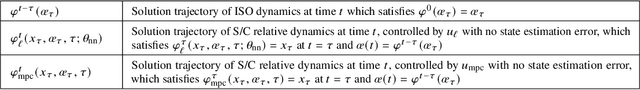
Interstellar objects (ISOs), astronomical objects not gravitationally bound to the Sun, are likely representatives of primitive materials invaluable in understanding exoplanetary star systems. Due to their poorly constrained orbits with generally high inclinations and relative velocities, however, exploring ISOs with conventional human-in-the-loop approaches is significantly challenging. This paper presents Neural-Rendezvous -- a deep learning-based guidance and control framework for encountering any fast-moving objects, including ISOs, robustly, accurately, and autonomously in real-time. It uses pointwise minimum norm tracking control on top of a guidance policy modeled by a spectrally-normalized deep neural network, where its hyperparameters are tuned with a newly introduced loss function directly penalizing the state trajectory tracking error. We rigorously show that, even in the challenging case of ISO exploration, Neural-Rendezvous provides 1) a high probability exponential bound on the expected spacecraft delivery error; and 2) a finite optimality gap with respect to the solution of model predictive control, both of which are indispensable especially for such a critical space mission. In numerical simulations, Neural-Rendezvous is demonstrated to achieve a terminal-time delivery error of less than 0.2 km for 99% of the ISO candidates with realistic state uncertainty, whilst retaining computational efficiency sufficient for real-time implementation.

A Theoretical Overview of Neural Contraction Metrics for Learning-based Control with Guaranteed Stability

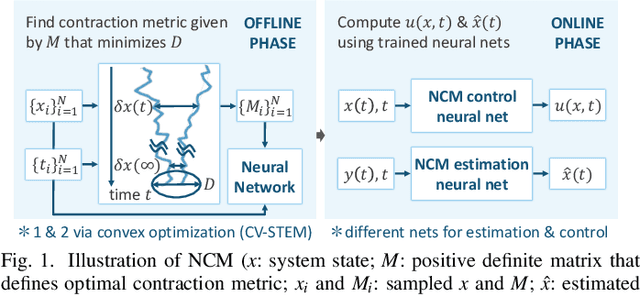
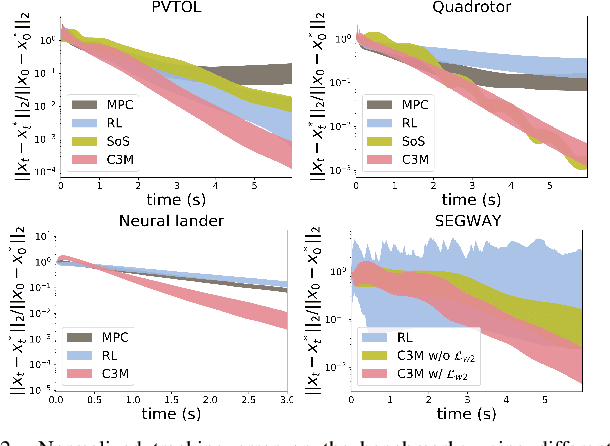
This paper presents a theoretical overview of a Neural Contraction Metric (NCM): a neural network model of an optimal contraction metric and corresponding differential Lyapunov function, the existence of which is a necessary and sufficient condition for incremental exponential stability of non-autonomous nonlinear system trajectories. Its innovation lies in providing formal robustness guarantees for learning-based control frameworks, utilizing contraction theory as an analytical tool to study the nonlinear stability of learned systems via convex optimization. In particular, we rigorously show in this paper that, by regarding modeling errors of the learning schemes as external disturbances, the NCM control is capable of obtaining an explicit bound on the distance between a time-varying target trajectory and perturbed solution trajectories, which exponentially decreases with time even under the presence of deterministic and stochastic perturbation. These useful features permit simultaneous synthesis of a contraction metric and associated control law by a neural network, thereby enabling real-time computable and probably robust learning-based control for general control-affine nonlinear systems.

Contraction Theory for Nonlinear Stability Analysis and Learning-based Control: A Tutorial Overview

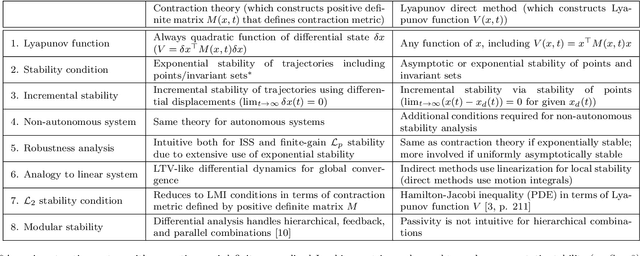
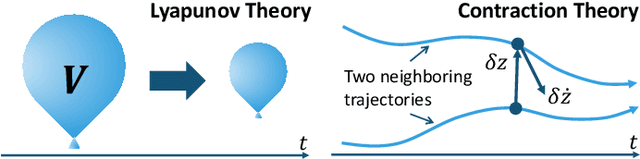
Contraction theory is an analytical tool to study differential dynamics of a non-autonomous (i.e., time-varying) nonlinear system under a contraction metric defined with a uniformly positive definite matrix, the existence of which results in a necessary and sufficient characterization of incremental exponential stability of multiple solution trajectories with respect to each other. By using a squared differential length as a Lyapunov-like function, its nonlinear stability analysis boils down to finding a suitable contraction metric that satisfies a stability condition expressed as a linear matrix inequality, indicating that many parallels can be drawn between well-known linear systems theory and contraction theory for nonlinear systems. Furthermore, contraction theory takes advantage of a superior robustness property of exponential stability used in conjunction with the comparison lemma. This yields much-needed safety and stability guarantees for neural network-based control and estimation schemes, without resorting to a more involved method of using uniform asymptotic stability for input-to-state stability. Such distinctive features permit systematic construction of a contraction metric via convex optimization, thereby obtaining an explicit exponential bound on the distance between a time-varying target trajectory and solution trajectories perturbed externally due to disturbances and learning errors. The objective of this paper is therefore to present a tutorial overview of contraction theory and its advantages in nonlinear stability analysis of deterministic and stochastic systems, with an emphasis on deriving formal robustness and stability guarantees for various learning-based and data-driven automatic control methods. In particular, we provide a detailed review of techniques for finding contraction metrics and associated control and estimation laws using deep neural networks.

Learning-based Adaptive Control via Contraction Theory

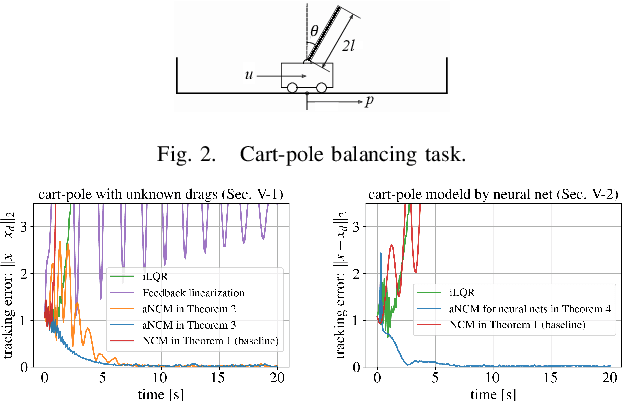
We present a new deep learning-based adaptive control framework for nonlinear systems with multiplicatively-separable parametric uncertainty, called an adaptive Neural Contraction Metric (aNCM). The aNCM uses a neural network model of an optimal adaptive contraction metric, the existence of which guarantees asymptotic stability and exponential boundedness of system trajectories under the parametric uncertainty. In particular, we exploit the concept of a Neural Contraction Metric (NCM) to obtain a nominal provably stable robust control policy for nonlinear systems with bounded disturbances, and combine this policy with a novel adaptation law to achieve stability guarantees. We also show that the framework is applicable to adaptive control of dynamical systems modeled via basis function approximation. Furthermore, the use of neural networks in the aNCM permits its real-time implementation, resulting in broad applicability to a variety of systems. Its superiority to the state-of-the-art is illustrated with a simple cart-pole balancing task.

Imitation Learning for Robust and Safe Real-time Motion Planning: A Contraction Theory Approach

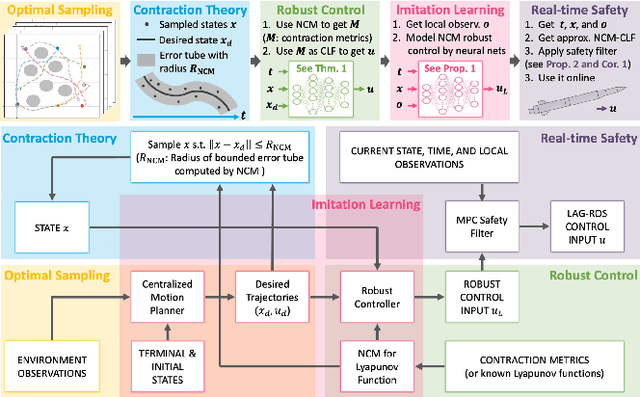
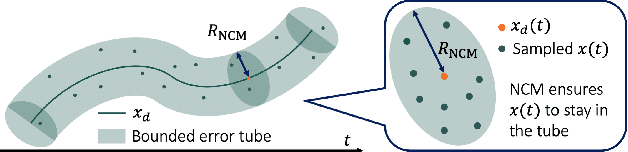
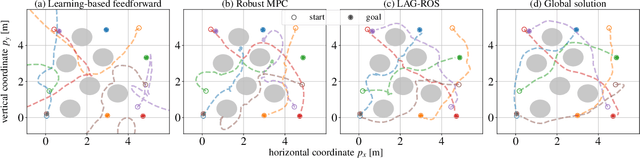
This paper presents Learning-based Autonomous Guidance with Robustness, Optimality, and Safety guarantees (LAG-ROS), a real-time robust motion planning algorithm for safety-critical nonlinear systems perturbed by bounded disturbances. The LAG-ROS method consists of three phases: 1) Control Lyapunov Function (CLF) construction via contraction theory; 2) imitation learning of the CLF-based robust feedback motion planner; and 3) its real-time and decentralized implementation with a learning-based model predictive safety filter. For the CLF, we exploit a neural-network-based method of Neural Contraction Metrics (NCMs), which provides a differential Lyapunov function to minimize an upper bound of the steady-state Euclidean distance between perturbed and unperturbed system trajectories. The NCM ensures the perturbed state to stay in bounded error tubes around given desired trajectories, where we sample training data for imitation learning of the NCM-CLF-based robust centralized motion planner. Using local observations in training also enables its decentralized implementation. Simulation results for perturbed nonlinear systems show that the LAG-ROS achieves higher control performance and task success rate with faster execution speed for real-time computation, when compared with the existing real-time robust MPC and learning-based feedforward motion planners.

Neural Stochastic Contraction Metrics for Robust Control and Estimation

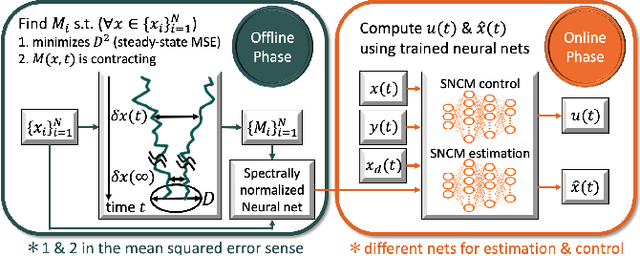
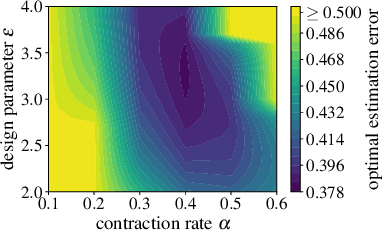
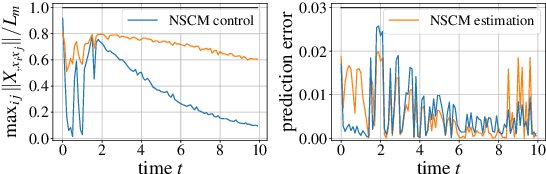
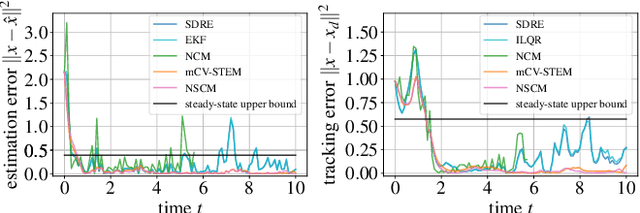
We present neural stochastic contraction metrics, a new design framework for provably-stable robust control and estimation for a class of stochastic nonlinear systems. It exploits a spectrally-normalized deep neural network to construct a contraction metric, sampled via simplified convex optimization in the stochastic setting. Spectral normalization constrains the state-derivatives of the metric to be Lipschitz continuous, and thereby ensures exponential boundedness of the mean squared distance of system trajectories under stochastic disturbances. This framework allows autonomous agents to approximate optimal stable control and estimation policies in real-time, and outperforms existing nonlinear control and estimation techniques including the state-dependent Riccati equation, iterative LQR, EKF, and deterministic neural contraction metric method, as illustrated in simulations.