Combining Movement Primitives with Contraction Theory

This paper presents a modular framework for motion planning using movement primitives. Central to the approach is Contraction Theory, a modular stability tool for nonlinear dynamical systems. The approach extends prior methods by achieving parallel and sequential combinations of both discrete and rhythmic movements, while enabling independent modulation of each movement. This modular framework enables a divide-and-conquer strategy to simplify the programming of complex robot motion planning. Simulation examples illustrate the flexibility and versatility of the framework, highlighting its potential to address diverse challenges in robot motion planning.

Quaternion Sliding Variables in Manipulator Control

We present two quaternion-based sliding variables for controlling the orientation of a manipulator's end-effector. Both sliding variables are free of singularities and represent global exponentially convergent error dynamics that do not exhibit unwinding when used in feedback. The choice of sliding variable is dictated by whether the end-effector's angular velocity vector is expressed in a local or global frame, and is a matter of convenience. Using quaternions allows the end-effector to move in its full operational envelope, which is not possible with other representations, e.g., Euler angles, that introduce representation-specific singularities. Further, the presented stability results are global rather than almost global, where the latter is often the best one can achieve when using rotation matrices to represent orientation.

URDF+: An Enhanced URDF for Robots with Kinematic Loops

Designs incorporating kinematic loops are becoming increasingly prevalent in the robotics community. Despite the existence of dynamics algorithms to deal with the effects of such loops, many modern simulators rely on dynamics libraries that require robots to be represented as kinematic trees. This requirement is reflected in the de facto standard format for describing robots, the Universal Robot Description Format (URDF), which does not support kinematic loops resulting in closed chains. This paper introduces an enhanced URDF, termed URDF+, which addresses this key shortcoming of URDF while retaining the intuitive design philosophy and low barrier to entry that the robotics community values. The URDF+ keeps the elements used by URDF to describe open chains and incorporates new elements to encode loop joints. We also offer an accompanying parser that processes the system models coming from URDF+ so that they can be used with recursive rigid-body dynamics algorithms for closed-chain systems that group bodies into local, decoupled loops. This parsing process is fully automated, ensuring optimal grouping of constrained bodies without requiring manual specification from the user. We aim to advance the robotics community towards this elegant solution by developing efficient and easy-to-use software tools.

Passive Obstacle Aware Control to Follow Desired Velocities

Evaluating and updating the obstacle avoidance velocity for an autonomous robot in real-time ensures robustness against noise and disturbances. A passive damping controller can obtain the desired motion with a torque-controlled robot, which remains compliant and ensures a safe response to external perturbations. Here, we propose a novel approach for designing the passive control policy. Our algorithm complies with obstacle-free zones while transitioning to increased damping near obstacles to ensure collision avoidance. This approach ensures stability across diverse scenarios, effectively mitigating disturbances. Validation on a 7DoF robot arm demonstrates superior collision rejection capabilities compared to the baseline, underlining its practicality for real-world applications. Our obstacle-aware damping controller represents a substantial advancement in secure robot control within complex and uncertain environments.

Dynamic Adaptation Gains for Nonlinear Systems with Unmatched Uncertainties

We present a new direct adaptive control approach for nonlinear systems with unmatched and matched uncertainties. The method relies on adjusting the adaptation gains of individual unmatched parameters whose adaptation transients would otherwise destabilize the closed-loop system. The approach also guarantees the restoration of the adaptation gains to their nominal values and can readily incorporate direct adaptation laws for matched uncertainties. The proposed framework is general as it only requires stabilizability for all possible models.

Stable Modular Control via Contraction Theory for Reinforcement Learning

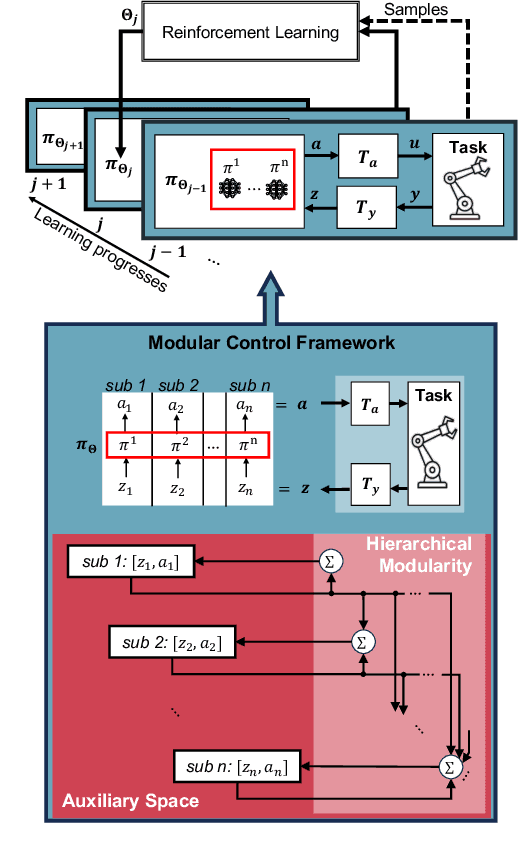
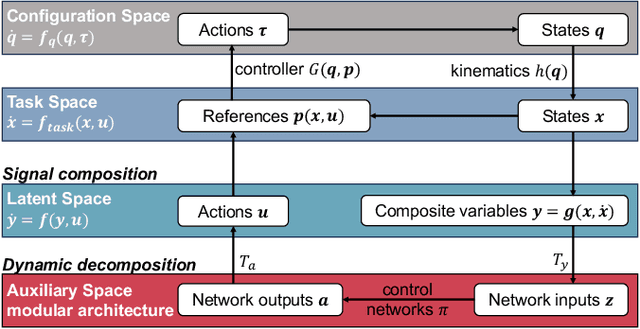
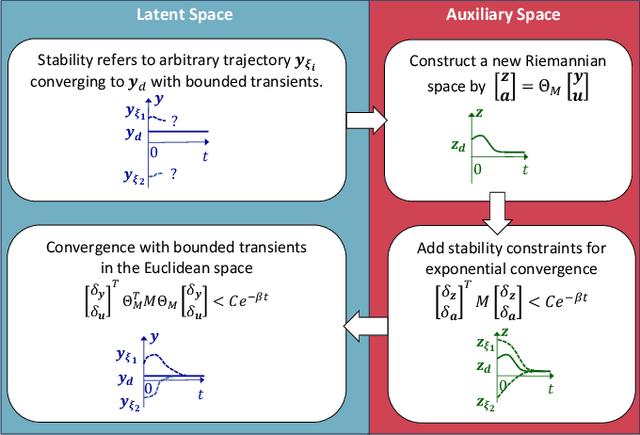
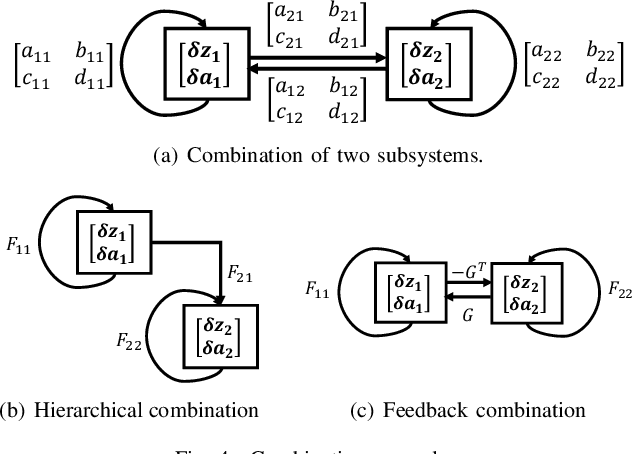
We propose a novel way to integrate control techniques with reinforcement learning (RL) for stability, robustness, and generalization: leveraging contraction theory to realize modularity in neural control, which ensures that combining stable subsystems can automatically preserve the stability. We realize such modularity via signal composition and dynamic decomposition. Signal composition creates the latent space, within which RL applies to maximizing rewards. Dynamic decomposition is realized by coordinate transformation that creates an auxiliary space, within which the latent signals are coupled in the way that their combination can preserve stability provided each signal, that is, each subsystem, has stable self-feedbacks. Leveraging modularity, the nonlinear stability problem is deconstructed into algebraically solvable ones, the stability of the subsystems in the auxiliary space, yielding linear constraints on the input gradients of control networks that can be as simple as switching the signs of network weights. This minimally invasive method for stability allows arguably easy integration into the modular neural architectures in machine learning, like hierarchical RL, and improves their performance. We demonstrate in simulation the necessity and the effectiveness of our method: the necessity for robustness and generalization, and the effectiveness in improving hierarchical RL for manipulation learning.

Contraction Properties of the Global Workspace Primitive

To push forward the important emerging research field surrounding multi-area recurrent neural networks (RNNs), we expand theoretically and empirically on the provably stable RNNs of RNNs introduced by Kozachkov et al. in "RNNs of RNNs: Recursive Construction of Stable Assemblies of Recurrent Neural Networks". We prove relaxed stability conditions for salient special cases of this architecture, most notably for a global workspace modular structure. We then demonstrate empirical success for Global Workspace Sparse Combo Nets with a small number of trainable parameters, not only through strong overall test performance but also greater resilience to removal of individual subnetworks. These empirical results for the global workspace inter-area topology are contingent on stability preservation, highlighting the relevance of our theoretical work for enabling modular RNN success. Further, by exploring sparsity in the connectivity structure between different subnetwork modules more broadly, we improve the state of the art performance for stable RNNs on benchmark sequence processing tasks, thus underscoring the general utility of specialized graph structures for multi-area RNNs.

Avoidance of Concave Obstacles through Rotation of Nonlinear Dynamics

Controlling complex tasks in robotic systems, such as circular motion for cleaning or following curvy lines, can be dealt with using nonlinear vector fields. In this paper, we introduce a novel approach called rotational obstacle avoidance method (ROAM) for adapting the initial dynamics when the workspace is partially occluded by obstacles. ROAM presents a closed-form solution that effectively avoids star-shaped obstacles in spaces of arbitrary dimensions by rotating the initial dynamics towards the tangent space. The algorithm enables navigation within obstacle hulls and can be customized to actively move away from surfaces, while guaranteeing the presence of only a single saddle point on the boundary of each obstacle. We introduce a sequence of mappings to extend the approach for general nonlinear dynamics. Moreover, ROAM extends its capabilities to handle multi-obstacle environments and provides the ability to constrain dynamics within a safe tube. By utilizing weighted vector-tree summation, we successfully navigate around general concave obstacles represented as a tree-of-stars. Through experimental evaluation, ROAM demonstrates superior performance in terms of minimizing occurrences of local minima and maintaining similarity to the initial dynamics, outperforming existing approaches in multi-obstacle simulations. The proposed method is highly reactive, owing to its simplicity, and can be applied effectively in dynamic environments. This was demonstrated during the collision-free navigation of a 7 degree-of-freedom robot arm around dynamic obstacles

MinMax Networks

While much progress has been achieved over the last decades in neuro-inspired machine learning, there are still fundamental theoretical problems in gradient-based learning using combinations of neurons. These problems, such as saddle points and suboptimal plateaus of the cost function, can lead in theory and practice to failures of learning. In addition, the discrete step size selection of the gradient is problematic since too large steps can lead to instability and too small steps slow down the learning. This paper describes an alternative discrete MinMax learning approach for continuous piece-wise linear functions. Global exponential convergence of the algorithm is established using Contraction Theory with Inequality Constraints, which is extended from the continuous to the discrete case in this paper: The parametrization of each linear function piece is, in contrast to deep learning, linear in the proposed MinMax network. This allows a linear regression stability proof as long as measurements do not transit from one linear region to its neighbouring linear region. The step size of the discrete gradient descent is Lagrangian limited orthogonal to the edge of two neighbouring linear functions. It will be shown that this Lagrangian step limitation does not decrease the convergence of the unconstrained system dynamics in contrast to a step size limitation in the direction of the gradient. We show that the convergence rate of a constrained piece-wise linear function learning is equivalent to the exponential convergence rates of the individual local linear regions.

Agile Catching with Whole-Body MPC and Blackbox Policy Learning

We address a benchmark task in agile robotics: catching objects thrown at high-speed. This is a challenging task that involves tracking, intercepting, and cradling a thrown object with access only to visual observations of the object and the proprioceptive state of the robot, all within a fraction of a second. We present the relative merits of two fundamentally different solution strategies: (i) Model Predictive Control using accelerated constrained trajectory optimization, and (ii) Reinforcement Learning using zeroth-order optimization. We provide insights into various performance trade-offs including sample efficiency, sim-to-real transfer, robustness to distribution shifts, and whole-body multimodality via extensive on-hardware experiments. We conclude with proposals on fusing "classical" and "learning-based" techniques for agile robot control. Videos of our experiments may be found at https://sites.google.com/view/agile-catching