Leo Kozachkov
NRGPT: An Energy-based Alternative for GPT
Dec 18, 2025Abstract:Generative Pre-trained Transformer (GPT) architectures are the most popular design for language modeling. Energy-based modeling is a different paradigm that views inference as a dynamical process operating on an energy landscape. We propose a minimal modification of the GPT setting to unify it with the EBM framework. The inference step of our model, which we call eNeRgy-GPT (NRGPT), is conceptualized as an exploration of the tokens on the energy landscape. We prove, and verify empirically, that under certain circumstances this exploration becomes gradient descent, although they don't necessarily lead to the best performing models. We demonstrate that our model performs well for simple language (Shakespeare dataset), algebraic ListOPS tasks, and richer settings such as OpenWebText language modeling. We also observe that our models may be more resistant to overfitting, doing so only during very long training.
InputDSA: Demixing then Comparing Recurrent and Externally Driven Dynamics
Oct 29, 2025Abstract:In control problems and basic scientific modeling, it is important to compare observations with dynamical simulations. For example, comparing two neural systems can shed light on the nature of emergent computations in the brain and deep neural networks. Recently, Ostrow et al. (2023) introduced Dynamical Similarity Analysis (DSA), a method to measure the similarity of two systems based on their recurrent dynamics rather than geometry or topology. However, DSA does not consider how inputs affect the dynamics, meaning that two similar systems, if driven differently, may be classified as different. Because real-world dynamical systems are rarely autonomous, it is important to account for the effects of input drive. To this end, we introduce a novel metric for comparing both intrinsic (recurrent) and input-driven dynamics, called InputDSA (iDSA). InputDSA extends the DSA framework by estimating and comparing both input and intrinsic dynamic operators using a variant of Dynamic Mode Decomposition with control (DMDc) based on subspace identification. We demonstrate that InputDSA can successfully compare partially observed, input-driven systems from noisy data. We show that when the true inputs are unknown, surrogate inputs can be substituted without a major deterioration in similarity estimates. We apply InputDSA on Recurrent Neural Networks (RNNs) trained with Deep Reinforcement Learning, identifying that high-performing networks are dynamically similar to one another, while low-performing networks are more diverse. Lastly, we apply InputDSA to neural data recorded from rats performing a cognitive task, demonstrating that it identifies a transition from input-driven evidence accumulation to intrinsically-driven decision-making. Our work demonstrates that InputDSA is a robust and efficient method for comparing intrinsic dynamics and the effect of external input on dynamical systems.
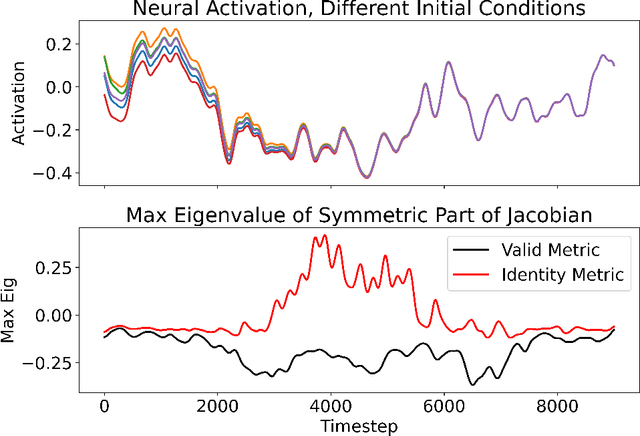
Characterizing control between interacting subsystems with deep Jacobian estimation
Jul 02, 2025Abstract:Biological function arises through the dynamical interactions of multiple subsystems, including those between brain areas, within gene regulatory networks, and more. A common approach to understanding these systems is to model the dynamics of each subsystem and characterize communication between them. An alternative approach is through the lens of control theory: how the subsystems control one another. This approach involves inferring the directionality, strength, and contextual modulation of control between subsystems. However, methods for understanding subsystem control are typically linear and cannot adequately describe the rich contextual effects enabled by nonlinear complex systems. To bridge this gap, we devise a data-driven nonlinear control-theoretic framework to characterize subsystem interactions via the Jacobian of the dynamics. We address the challenge of learning Jacobians from time-series data by proposing the JacobianODE, a deep learning method that leverages properties of the Jacobian to directly estimate it for arbitrary dynamical systems from data alone. We show that JacobianODEs outperform existing Jacobian estimation methods on challenging systems, including high-dimensional chaos. Applying our approach to a multi-area recurrent neural network (RNN) trained on a working memory selection task, we show that the "sensory" area gains greater control over the "cognitive" area over learning. Furthermore, we leverage the JacobianODE to directly control the trained RNN, enabling precise manipulation of its behavior. Our work lays the foundation for a theoretically grounded and data-driven understanding of interactions among biological subsystems.
Is All Learning (Natural) Gradient Descent?
Sep 24, 2024Abstract:This paper shows that a wide class of effective learning rules -- those that improve a scalar performance measure over a given time window -- can be rewritten as natural gradient descent with respect to a suitably defined loss function and metric. Specifically, we show that parameter updates within this class of learning rules can be expressed as the product of a symmetric positive definite matrix (i.e., a metric) and the negative gradient of a loss function. We also demonstrate that these metrics have a canonical form and identify several optimal ones, including the metric that achieves the minimum possible condition number. The proofs of the main results are straightforward, relying only on elementary linear algebra and calculus, and are applicable to continuous-time, discrete-time, stochastic, and higher-order learning rules, as well as loss functions that explicitly depend on time.
Contraction Properties of the Global Workspace Primitive
Oct 02, 2023Abstract:To push forward the important emerging research field surrounding multi-area recurrent neural networks (RNNs), we expand theoretically and empirically on the provably stable RNNs of RNNs introduced by Kozachkov et al. in "RNNs of RNNs: Recursive Construction of Stable Assemblies of Recurrent Neural Networks". We prove relaxed stability conditions for salient special cases of this architecture, most notably for a global workspace modular structure. We then demonstrate empirical success for Global Workspace Sparse Combo Nets with a small number of trainable parameters, not only through strong overall test performance but also greater resilience to removal of individual subnetworks. These empirical results for the global workspace inter-area topology are contingent on stability preservation, highlighting the relevance of our theoretical work for enabling modular RNN success. Further, by exploring sparsity in the connectivity structure between different subnetwork modules more broadly, we improve the state of the art performance for stable RNNs on benchmark sequence processing tasks, thus underscoring the general utility of specialized graph structures for multi-area RNNs.
Beyond Geometry: Comparing the Temporal Structure of Computation in Neural Circuits with Dynamical Similarity Analysis
Jun 16, 2023Abstract:How can we tell whether two neural networks are utilizing the same internal processes for a particular computation? This question is pertinent for multiple subfields of both neuroscience and machine learning, including neuroAI, mechanistic interpretability, and brain-machine interfaces. Standard approaches for comparing neural networks focus on the spatial geometry of latent states. Yet in recurrent networks, computations are implemented at the level of neural dynamics, which do not have a simple one-to-one mapping with geometry. To bridge this gap, we introduce a novel similarity metric that compares two systems at the level of their dynamics. Our method incorporates two components: Using recent advances in data-driven dynamical systems theory, we learn a high-dimensional linear system that accurately captures core features of the original nonlinear dynamics. Next, we compare these linear approximations via a novel extension of Procrustes Analysis that accounts for how vector fields change under orthogonal transformation. Via four case studies, we demonstrate that our method effectively identifies and distinguishes dynamic structure in recurrent neural networks (RNNs), whereas geometric methods fall short. We additionally show that our method can distinguish learning rules in an unsupervised manner. Our method therefore opens the door to novel data-driven analyses of the temporal structure of neural computation, and to more rigorous testing of RNNs as models of the brain.
Generalization in Supervised Learning Through Riemannian Contraction
Jan 26, 2022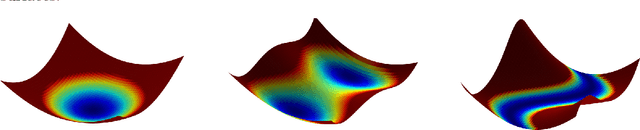

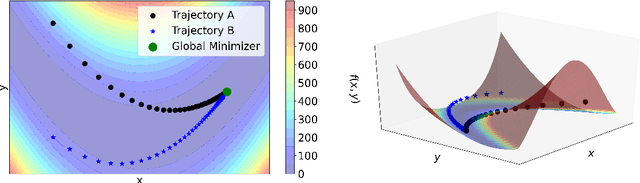

Abstract:We prove that Riemannian contraction in a supervised learning setting implies generalization. Specifically, we show that if an optimizer is contracting in some Riemannian metric with rate $\lambda > 0$, it is uniformly algorithmically stable with rate $\mathcal{O}(1/\lambda n)$, where $n$ is the number of labelled examples in the training set. The results hold for stochastic and deterministic optimization, in both continuous and discrete-time, for convex and non-convex loss surfaces. The associated generalization bounds reduce to well-known results in the particular case of gradient descent over convex or strongly convex loss surfaces. They can be shown to be optimal in certain linear settings, such as kernel ridge regression under gradient flow.
Recursive Construction of Stable Assemblies of Recurrent Neural Networks
Jun 16, 2021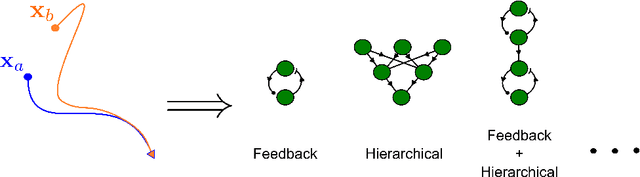
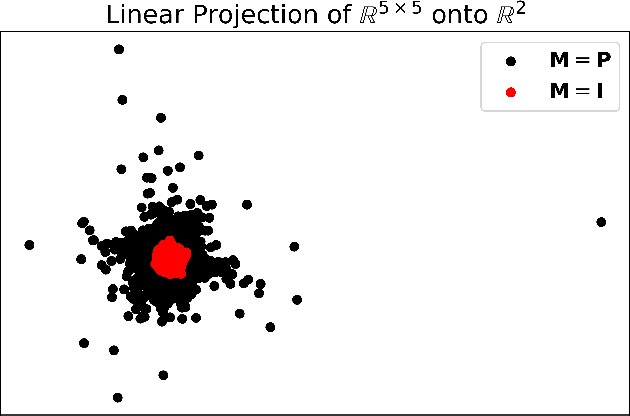
Abstract:Advanced applications of modern machine learning will likely involve combinations of trained networks, as are already used in spectacular systems such as DeepMind's AlphaGo. Recursively building such combinations in an effective and stable fashion while also allowing for continual refinement of the individual networks - as nature does for biological networks - will require new analysis tools. This paper takes a step in this direction by establishing contraction properties of broad classes of nonlinear recurrent networks and neural ODEs, and showing how these quantified properties allow in turn to recursively construct stable networks of networks in a systematic fashion. The results can also be used to stably combine recurrent networks and physical systems with quantified contraction properties. Similarly, they may be applied to modular computational models of cognition.
The Causal Role of Astrocytes in Slow-Wave Rhythmogenesis: A Computational Modelling Study
Feb 13, 2017
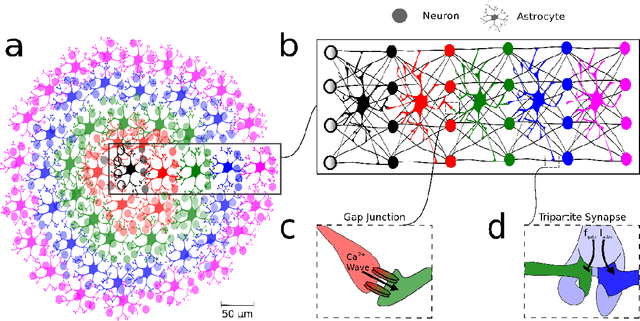


Abstract:Finding the origin of slow and infra-slow oscillations could reveal or explain brain mechanisms in health and disease. Here, we present a biophysically constrained computational model of a neural network where the inclusion of astrocytes introduced slow and infra-slow-oscillations, through two distinct mechanisms. Specifically, we show how astrocytes can modulate the fast network activity through their slow inter-cellular calcium wave speed and amplitude and possibly cause the oscillatory imbalances observed in diseases commonly known for such abnormalities, namely Alzheimer's disease, Parkinson's disease, epilepsy, depression and ischemic stroke. This work aims to increase our knowledge on how astrocytes and neurons synergize to affect brain function and dysfunction.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge