Is All Learning (Natural) Gradient Descent?

This paper shows that a wide class of effective learning rules -- those that improve a scalar performance measure over a given time window -- can be rewritten as natural gradient descent with respect to a suitably defined loss function and metric. Specifically, we show that parameter updates within this class of learning rules can be expressed as the product of a symmetric positive definite matrix (i.e., a metric) and the negative gradient of a loss function. We also demonstrate that these metrics have a canonical form and identify several optimal ones, including the metric that achieves the minimum possible condition number. The proofs of the main results are straightforward, relying only on elementary linear algebra and calculus, and are applicable to continuous-time, discrete-time, stochastic, and higher-order learning rules, as well as loss functions that explicitly depend on time.

Complex sequencing rules of birdsong can be explained by simple hidden Markov processes

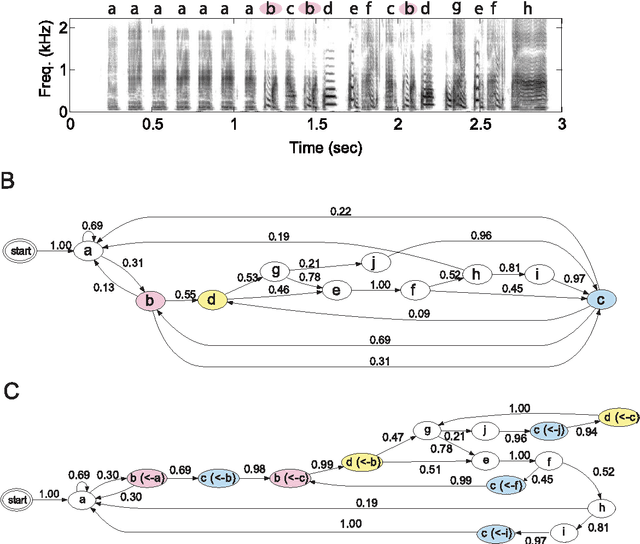
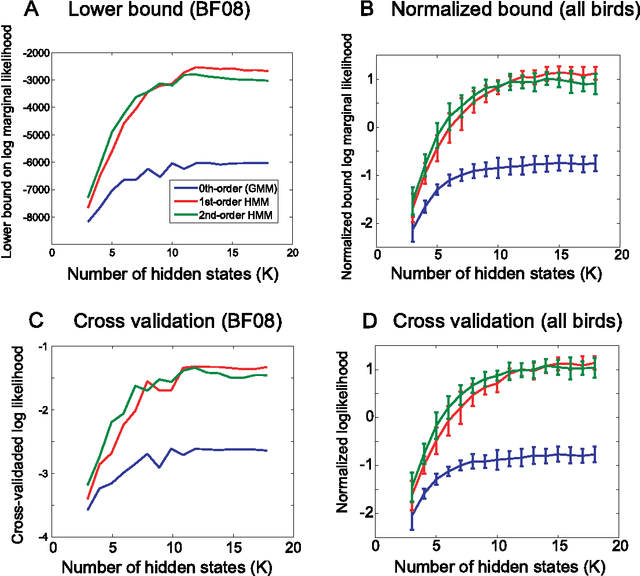
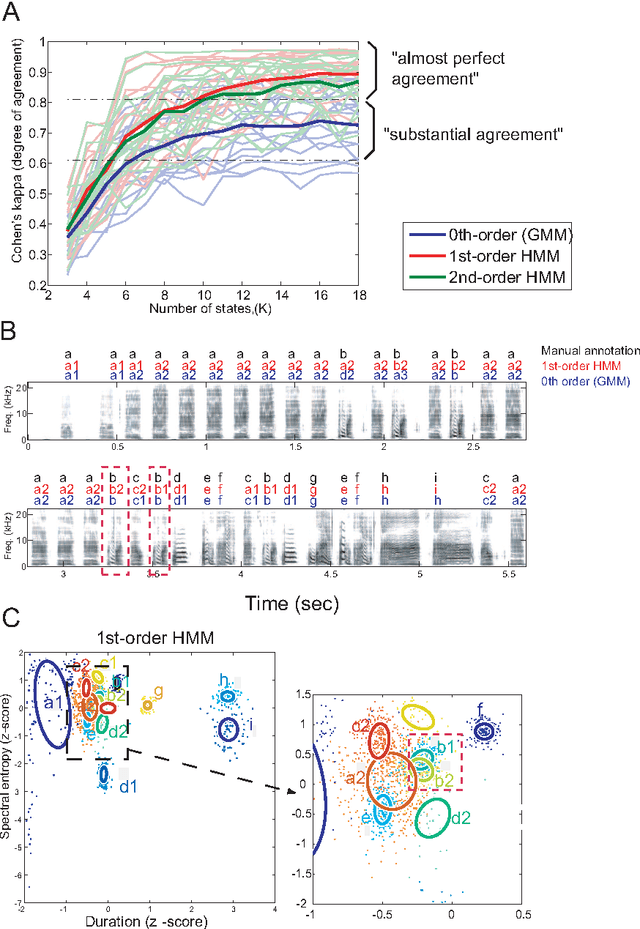
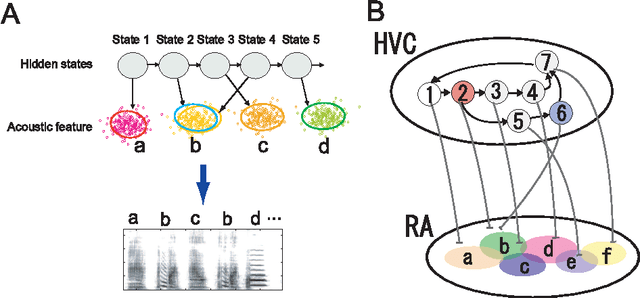
Complex sequencing rules observed in birdsongs provide an opportunity to investigate the neural mechanism for generating complex sequential behaviors. To relate the findings from studying birdsongs to other sequential behaviors, it is crucial to characterize the statistical properties of the sequencing rules in birdsongs. However, the properties of the sequencing rules in birdsongs have not yet been fully addressed. In this study, we investigate the statistical propertiesof the complex birdsong of the Bengalese finch (Lonchura striata var. domestica). Based on manual-annotated syllable sequences, we first show that there are significant higher-order context dependencies in Bengalese finch songs, that is, which syllable appears next depends on more than one previous syllable. This property is shared with other complex sequential behaviors. We then analyze acoustic features of the song and show that higher-order context dependencies can be explained using first-order hidden state transition dynamics with redundant hidden states. This model corresponds to hidden Markov models (HMMs), well known statistical models with a large range of application for time series modeling. The song annotation with these models with first-order hidden state dynamics agreed well with manual annotation, the score was comparable to that of a second-order HMM, and surpassed the zeroth-order model (the Gaussian mixture model (GMM)), which does not use context information. Our results imply that the hierarchical representation with hidden state dynamics may underlie the neural implementation for generating complex sequences with higher-order dependencies.