Sequential Experimental Design for Spectral Measurement: Active Learning Using a Parametric Model

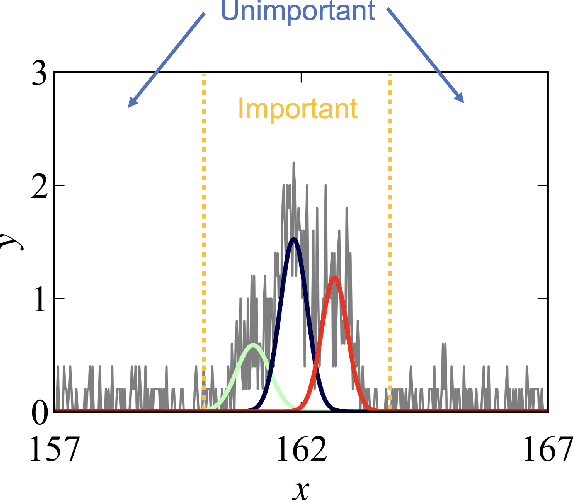
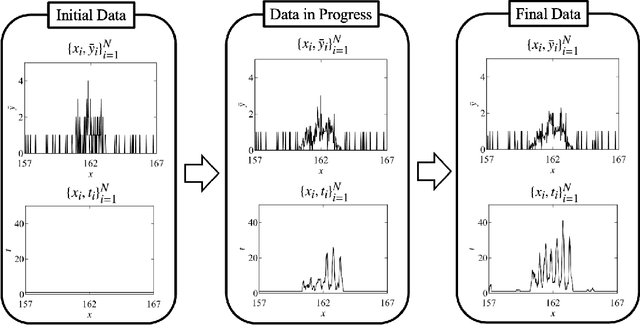
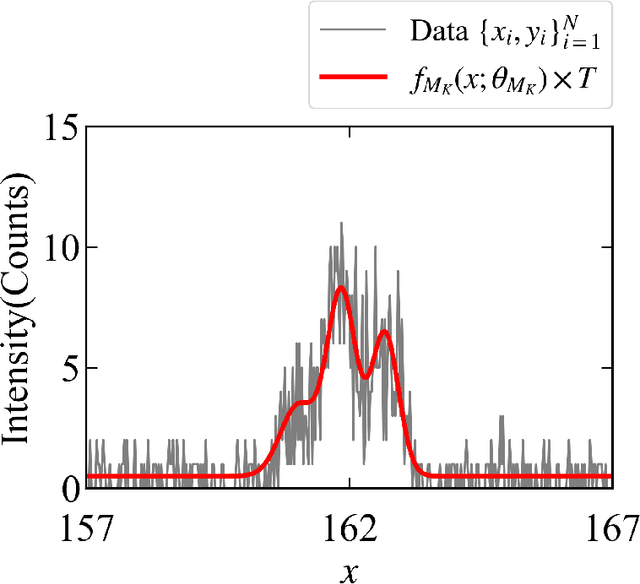
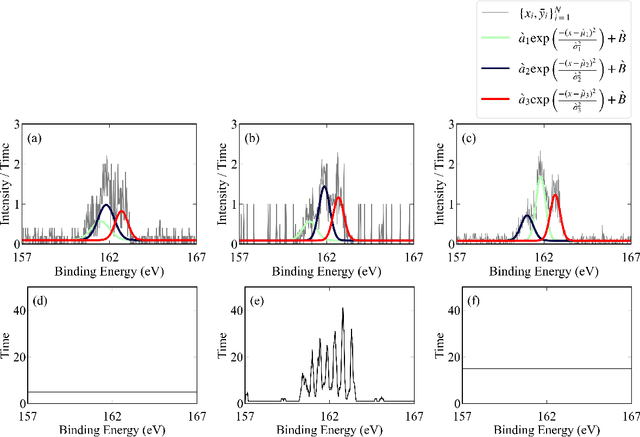
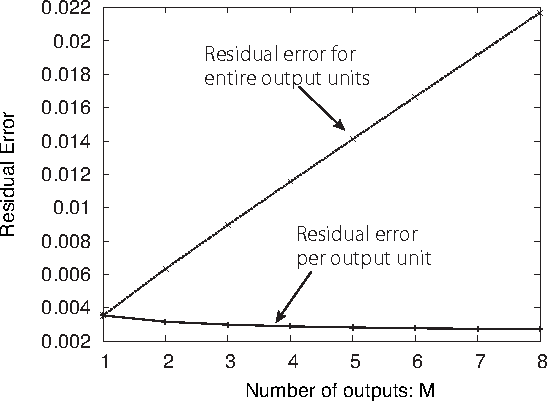
In this study, we demonstrate a sequential experimental design for spectral measurements by active learning using parametric models as predictors. In spectral measurements, it is necessary to reduce the measurement time because of sample fragility and high energy costs. To improve the efficiency of experiments, sequential experimental designs are proposed, in which the subsequent measurement is designed by active learning using the data obtained before the measurement. Conventionally, parametric models are employed in data analysis; when employed for active learning, they are expected to afford a sequential experimental design that improves the accuracy of data analysis. However, due to the complexity of the formulas, a sequential experimental design using general parametric models has not been realized. Therefore, we applied Bayesian inference-based data analysis using the exchange Monte Carlo method to realize a sequential experimental design with general parametric models. In this study, we evaluated the effectiveness of the proposed method by applying it to Bayesian spectral deconvolution and Bayesian Hamiltonian selection in X-ray photoelectron spectroscopy. Using numerical experiments with artificial data, we demonstrated that the proposed method improves the accuracy of model selection and parameter estimation while reducing the measurement time compared with the results achieved without active learning or with active learning using the Gaussian process regression.

Statistical Mechanical Analysis of Catastrophic Forgetting in Continual Learning with Teacher and Student Networks

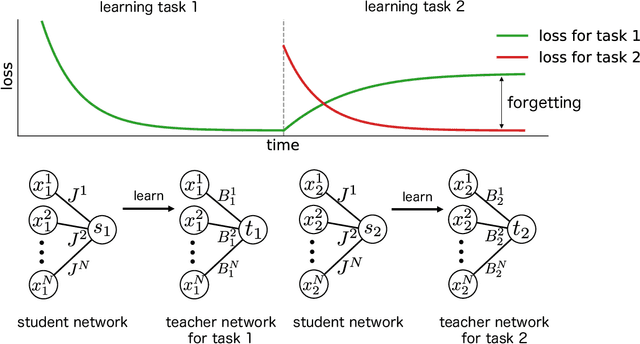
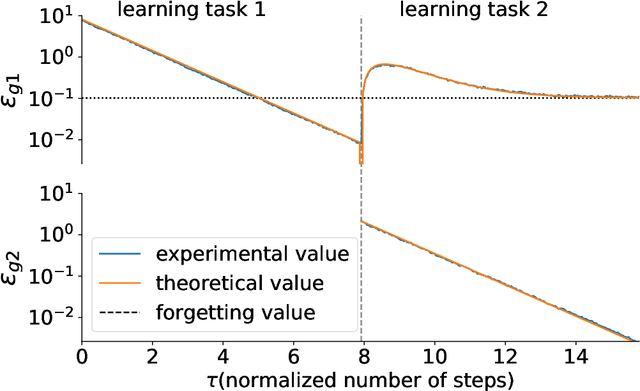
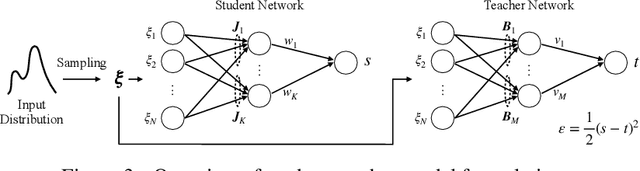
When a computational system continuously learns from an ever-changing environment, it rapidly forgets its past experiences. This phenomenon is called catastrophic forgetting. While a line of studies has been proposed with respect to avoiding catastrophic forgetting, most of the methods are based on intuitive insights into the phenomenon, and their performances have been evaluated by numerical experiments using benchmark datasets. Therefore, in this study, we provide the theoretical framework for analyzing catastrophic forgetting by using teacher-student learning. Teacher-student learning is a framework in which we introduce two neural networks: one neural network is a target function in supervised learning, and the other is a learning neural network. To analyze continual learning in the teacher-student framework, we introduce the similarity of the input distribution and the input-output relationship of the target functions as the similarity of tasks. In this theoretical framework, we also provide a qualitative understanding of how a single-layer linear learning neural network forgets tasks. Based on the analysis, we find that the network can avoid catastrophic forgetting when the similarity among input distributions is small and that of the input-output relationship of the target functions is large. The analysis also suggests that a system often exhibits a characteristic phenomenon called overshoot, which means that even if the learning network has once undergone catastrophic forgetting, it is possible that the network may perform reasonably well after further learning of the current task.

Data-Dependence of Plateau Phenomenon in Learning with Neural Network --- Statistical Mechanical Analysis

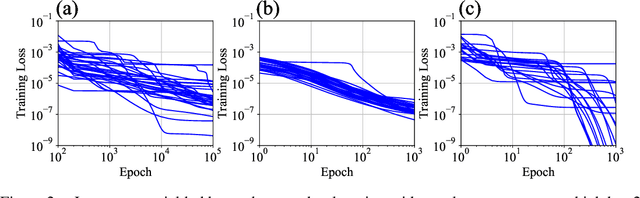
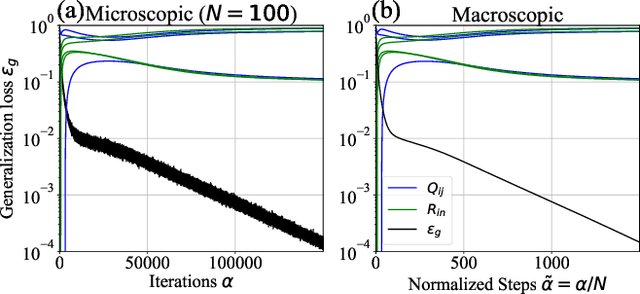
The plateau phenomenon, wherein the loss value stops decreasing during the process of learning, has been reported by various researchers. The phenomenon is actively inspected in the 1990s and found to be due to the fundamental hierarchical structure of neural network models. Then the phenomenon has been thought as inevitable. However, the phenomenon seldom occurs in the context of recent deep learning. There is a gap between theory and reality. In this paper, using statistical mechanical formulation, we clarified the relationship between the plateau phenomenon and the statistical property of the data learned. It is shown that the data whose covariance has small and dispersed eigenvalues tend to make the plateau phenomenon inconspicuous.

Bayesian Spectral Deconvolution Based on Poisson Distribution: Bayesian Measurement and Virtual Measurement Analytics (VMA)

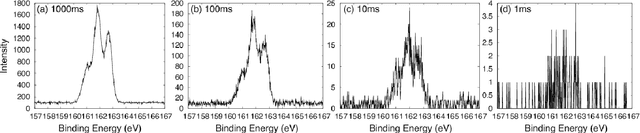
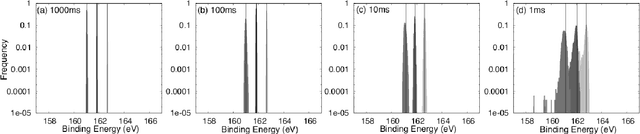
In this paper, we propose a new method of Bayesian measurement for spectral deconvolution, which regresses spectral data into the sum of unimodal basis function such as Gaussian or Lorentzian functions. Bayesian measurement is a framework for considering not only the target physical model but also the measurement model as a probabilistic model, and enables us to estimate the parameter of a physical model with its confidence interval through a Bayesian posterior distribution given a measurement data set. The measurement with Poisson noise is one of the most effective system to apply our proposed method. Since the measurement time is strongly related to the signal-to-noise ratio for the Poisson noise model, Bayesian measurement with Poisson noise model enables us to clarify the relationship between the measurement time and the limit of estimation. In this study, we establish the probabilistic model with Poisson noise for spectral deconvolution. Bayesian measurement enables us to perform virtual and computer simulation for a certain measurement through the established probabilistic model. This property is called "Virtual Measurement Analytics(VMA)" in this paper. We also show that the relationship between the measurement time and the limit of estimation can be extracted by using the proposed method in a simulation of synthetic data and real data for XPS measurement of MoS$_2$.

Statistical mechanical analysis of sparse linear regression as a variable selection problem

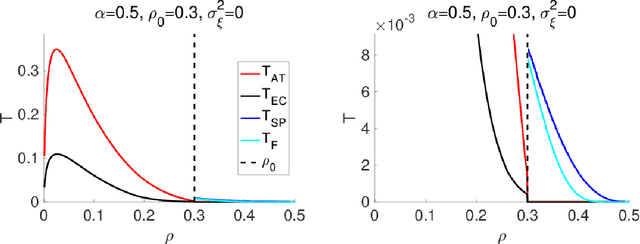
An algorithmic limit of compressed sensing or related variable-selection problems is analytically evaluated when a design matrix is given by an overcomplete random matrix. The replica method from statistical mechanics is employed to derive the result. The analysis is conducted through evaluation of the entropy, an exponential rate of the number of combinations of variables giving a specific value of fit error to given data which is assumed to be generated from a linear process using the design matrix. This yields the typical achievable limit of the fit error when solving a representative $\ell_0$ problem and includes the presence of unfavourable phase transitions preventing local search algorithms from reaching the minimum-error configuration. The associated phase diagrams are presented. A noteworthy outcome of the phase diagrams is that there exists a wide parameter region where any phase transition is absent from the high temperature to the lowest temperature at which the minimum-error configuration or the ground state is reached. This implies that certain local search algorithms can find the ground state with moderate computational costs in that region. Another noteworthy result is the presence of the random first-order transition in the strong noise case. The theoretical evaluation of the entropy is confirmed by extensive numerical methods using the exchange Monte Carlo and the multi-histogram methods. Another numerical test based on a metaheuristic optimisation algorithm called simulated annealing is conducted, which well supports the theoretical predictions on the local search algorithms. In the successful region with no phase transition, the computational cost of the simulated annealing to reach the ground state is estimated as the third order polynomial of the model dimensionality.

Concept Formation and Dynamics of Repeated Inference in Deep Generative Models

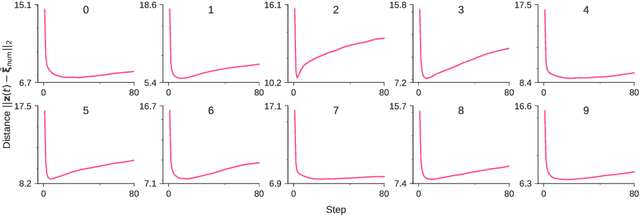
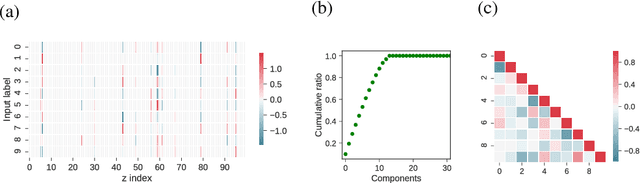
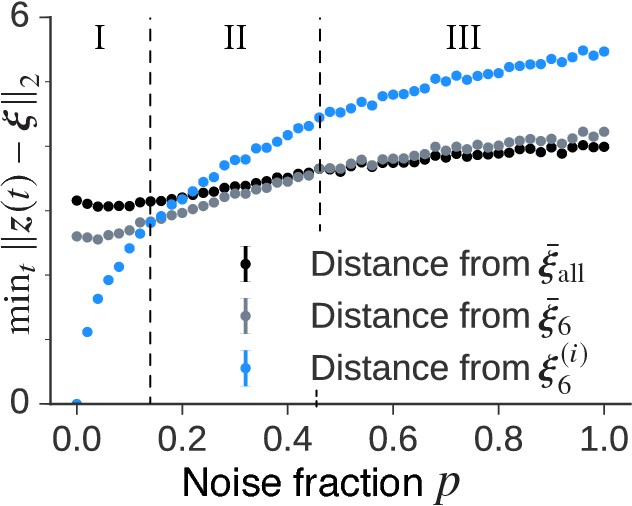
Deep generative models are reported to be useful in broad applications including image generation. Repeated inference between data space and latent space in these models can denoise cluttered images and improve the quality of inferred results. However, previous studies only qualitatively evaluated image outputs in data space, and the mechanism behind the inference has not been investigated. The purpose of the current study is to numerically analyze changes in activity patterns of neurons in the latent space of a deep generative model called a "variational auto-encoder" (VAE). What kinds of inference dynamics the VAE demonstrates when noise is added to the input data are identified. The VAE embeds a dataset with clear cluster structures in the latent space and the center of each cluster of multiple correlated data points (memories) is referred as the concept. Our study demonstrated that transient dynamics of inference first approaches a concept, and then moves close to a memory. Moreover, the VAE revealed that the inference dynamics approaches a more abstract concept to the extent that the uncertainty of input data increases due to noise. It was demonstrated that by increasing the number of the latent variables, the trend of the inference dynamics to approach a concept can be enhanced, and the generalization ability of the VAE can be improved.

Exhaustive search for sparse variable selection in linear regression

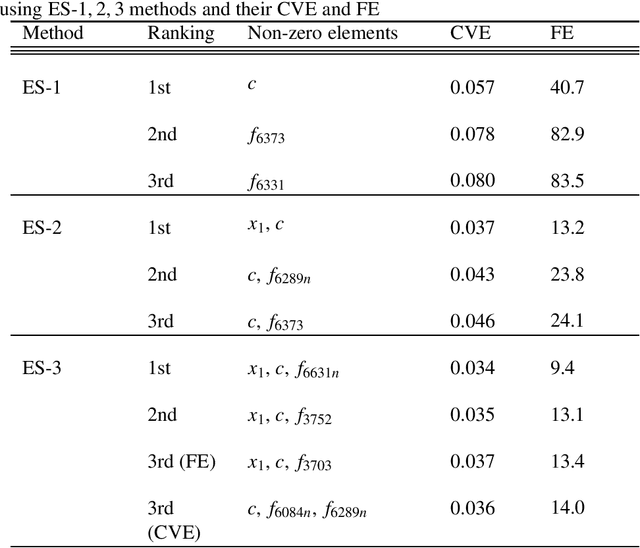
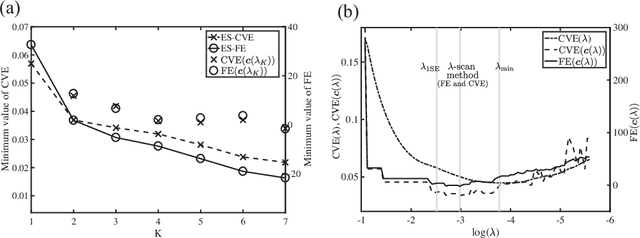
We propose a K-sparse exhaustive search (ES-K) method and a K-sparse approximate exhaustive search method (AES-K) for selecting variables in linear regression. With these methods, K-sparse combinations of variables are tested exhaustively assuming that the optimal combination of explanatory variables is K-sparse. By collecting the results of exhaustively computing ES-K, various approximate methods for selecting sparse variables can be summarized as density of states. With this density of states, we can compare different methods for selecting sparse variables such as relaxation and sampling. For large problems where the combinatorial explosion of explanatory variables is crucial, the AES-K method enables density of states to be effectively reconstructed by using the replica-exchange Monte Carlo method and the multiple histogram method. Applying the ES-K and AES-K methods to type Ia supernova data, we confirmed the conventional understanding in astronomy when an appropriate K is given beforehand. However, we found the difficulty to determine K from the data. Using virtual measurement and analysis, we argue that this is caused by data shortage.

Statistical Mechanics of Node-perturbation Learning with Noisy Baseline

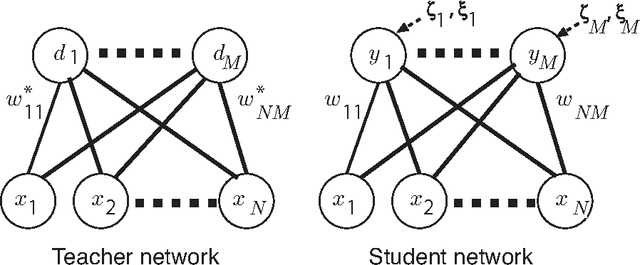
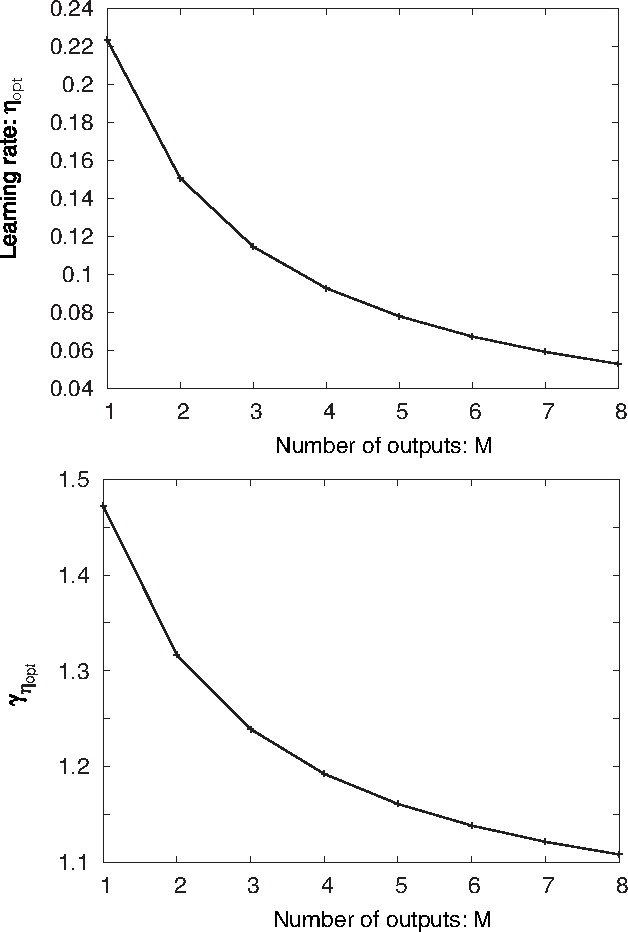
Node-perturbation learning is a type of statistical gradient descent algorithm that can be applied to problems where the objective function is not explicitly formulated, including reinforcement learning. It estimates the gradient of an objective function by using the change in the object function in response to the perturbation. The value of the objective function for an unperturbed output is called a baseline. Cho et al. proposed node-perturbation learning with a noisy baseline. In this paper, we report on building the statistical mechanics of Cho's model and on deriving coupled differential equations of order parameters that depict learning dynamics. We also show how to derive the generalization error by solving the differential equations of order parameters. On the basis of the results, we show that Cho's results are also apply in general cases and show some general performances of Cho's model.

Simultaneous Estimation of Noise Variance and Number of Peaks in Bayesian Spectral Deconvolution

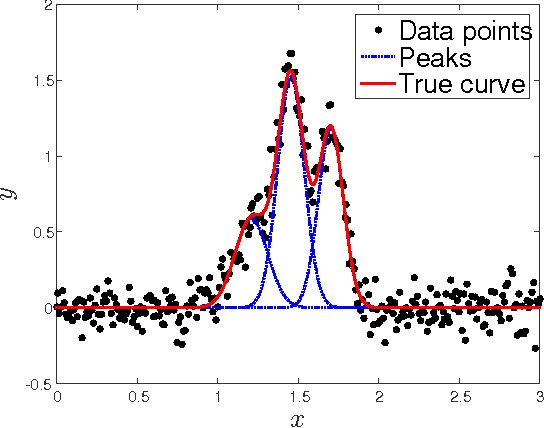
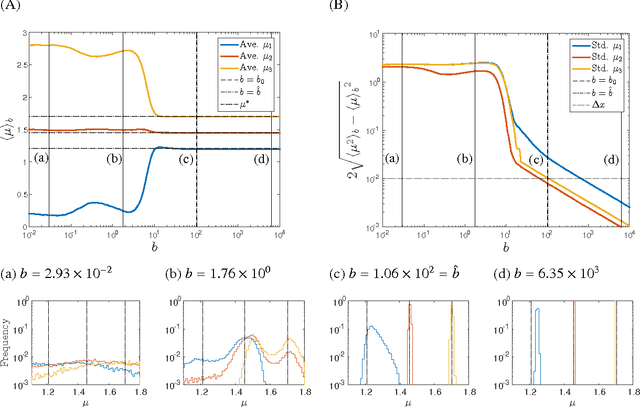
The heuristic identification of peaks from noisy complex spectra often leads to misunderstanding of the physical and chemical properties of matter. In this paper, we propose a framework based on Bayesian inference, which enables us to separate multipeak spectra into single peaks statistically and consists of two steps. The first step is estimating both the noise variance and the number of peaks as hyperparameters based on Bayes free energy, which generally is not analytically tractable. The second step is fitting the parameters of each peak function to the given spectrum by calculating the posterior density, which has a problem of local minima and saddles since multipeak models are nonlinear and hierarchical. Our framework enables the escape from local minima or saddles by using the exchange Monte Carlo method and calculates Bayes free energy via the multiple histogram method. We discuss a simulation demonstrating how efficient our framework is and show that estimating both the noise variance and the number of peaks prevents overfitting, overpenalizing, and misunderstanding the precision of parameter estimation.

Complex sequencing rules of birdsong can be explained by simple hidden Markov processes

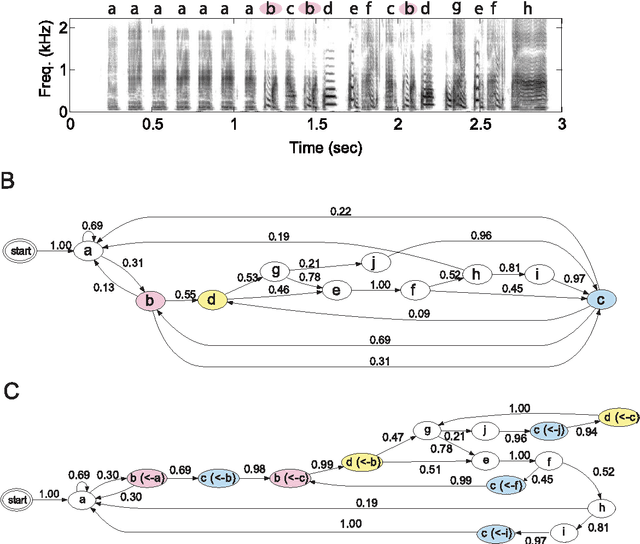
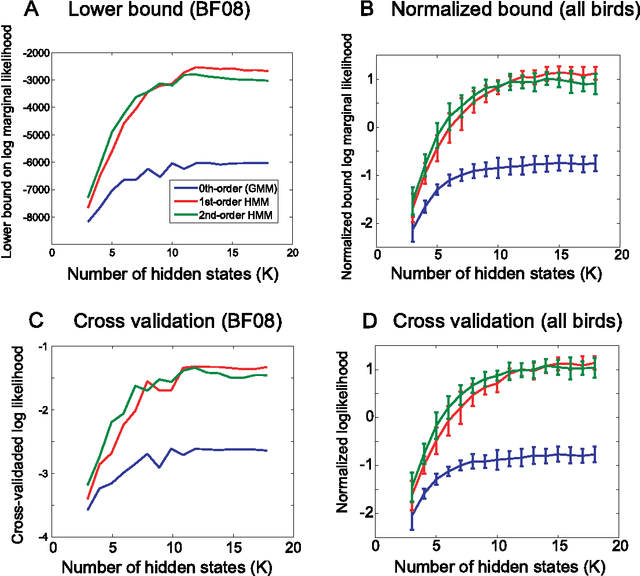
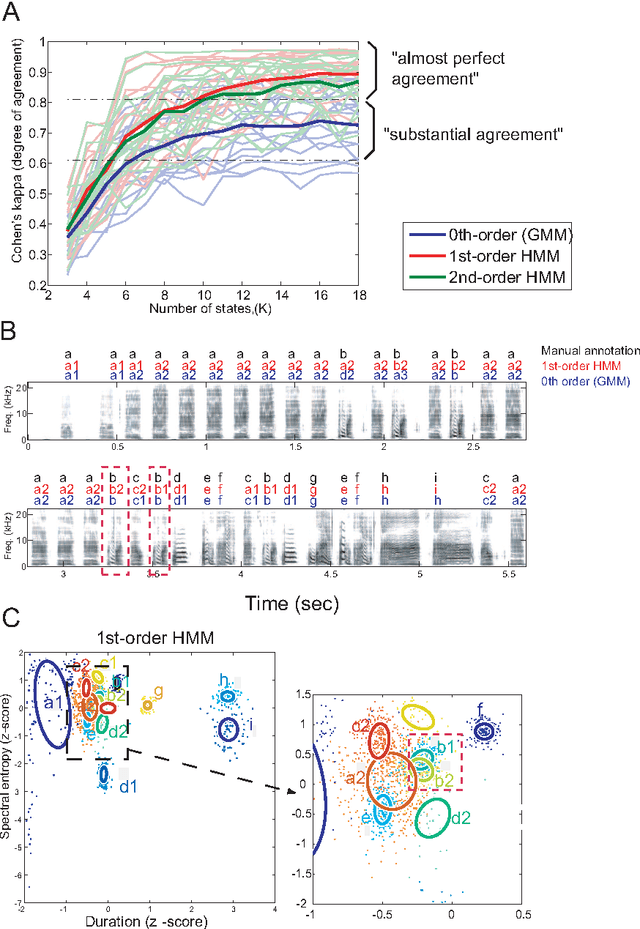
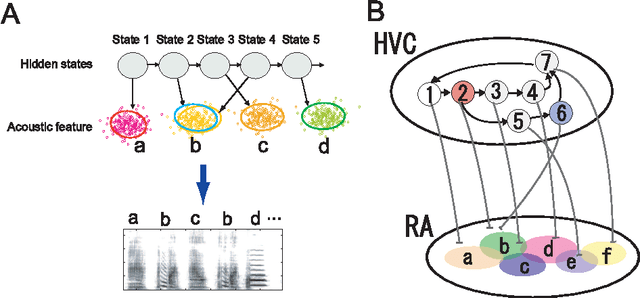
Complex sequencing rules observed in birdsongs provide an opportunity to investigate the neural mechanism for generating complex sequential behaviors. To relate the findings from studying birdsongs to other sequential behaviors, it is crucial to characterize the statistical properties of the sequencing rules in birdsongs. However, the properties of the sequencing rules in birdsongs have not yet been fully addressed. In this study, we investigate the statistical propertiesof the complex birdsong of the Bengalese finch (Lonchura striata var. domestica). Based on manual-annotated syllable sequences, we first show that there are significant higher-order context dependencies in Bengalese finch songs, that is, which syllable appears next depends on more than one previous syllable. This property is shared with other complex sequential behaviors. We then analyze acoustic features of the song and show that higher-order context dependencies can be explained using first-order hidden state transition dynamics with redundant hidden states. This model corresponds to hidden Markov models (HMMs), well known statistical models with a large range of application for time series modeling. The song annotation with these models with first-order hidden state dynamics agreed well with manual annotation, the score was comparable to that of a second-order HMM, and surpassed the zeroth-order model (the Gaussian mixture model (GMM)), which does not use context information. Our results imply that the hierarchical representation with hidden state dynamics may underlie the neural implementation for generating complex sequences with higher-order dependencies.