Statistical Mechanics of Node-perturbation Learning with Noisy Baseline
Paper and Code
Jun 20, 2017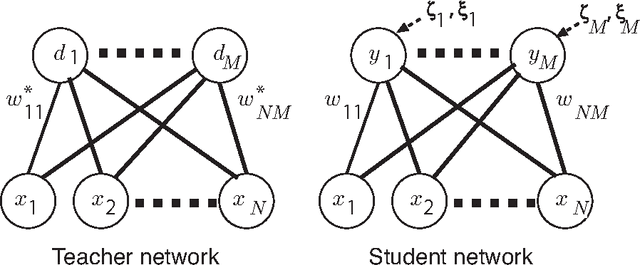
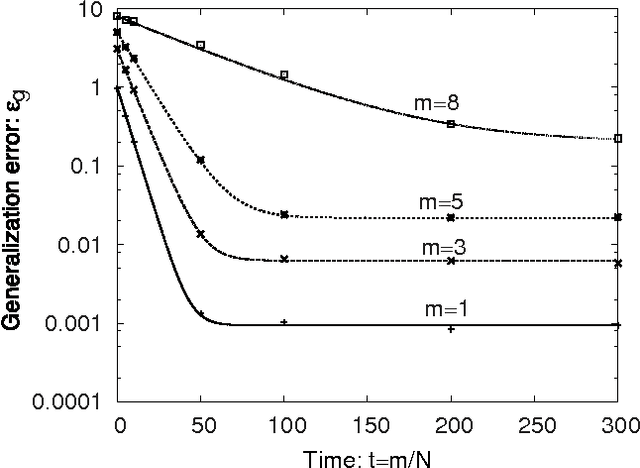
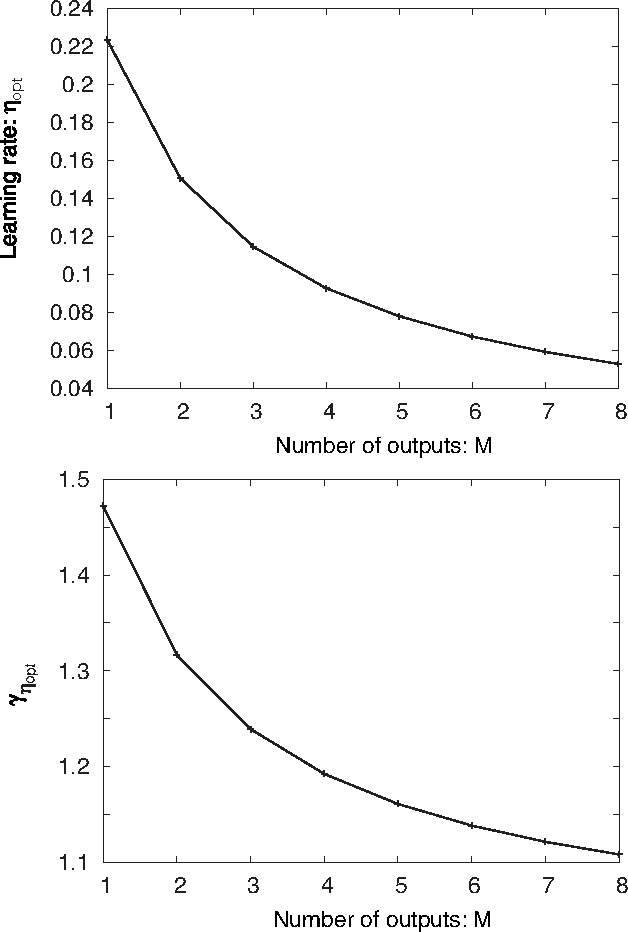
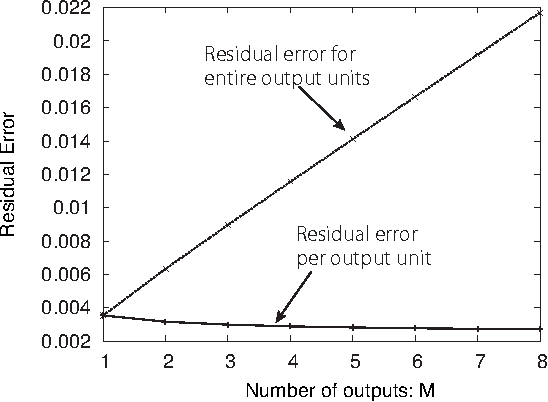
Node-perturbation learning is a type of statistical gradient descent algorithm that can be applied to problems where the objective function is not explicitly formulated, including reinforcement learning. It estimates the gradient of an objective function by using the change in the object function in response to the perturbation. The value of the objective function for an unperturbed output is called a baseline. Cho et al. proposed node-perturbation learning with a noisy baseline. In this paper, we report on building the statistical mechanics of Cho's model and on deriving coupled differential equations of order parameters that depict learning dynamics. We also show how to derive the generalization error by solving the differential equations of order parameters. On the basis of the results, we show that Cho's results are also apply in general cases and show some general performances of Cho's model.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge