Teaching Specific Scientific Knowledge into Large Language Models through Additional Training

Through additional training, we explore embedding specialized scientific knowledge into the Llama 2 Large Language Model (LLM). Key findings reveal that effective knowledge integration requires reading texts from multiple perspectives, especially in instructional formats. We utilize text augmentation to tackle the scarcity of specialized texts, including style conversions and translations. Hyperparameter optimization proves crucial, with different size models (7b, 13b, and 70b) reasonably undergoing additional training. Validating our methods, we construct a dataset of 65,000 scientific papers. Although we have succeeded in partially embedding knowledge, the study highlights the complexities and limitations of incorporating specialized information into LLMs, suggesting areas for further improvement.

Statistical Mechanical Analysis of Catastrophic Forgetting in Continual Learning with Teacher and Student Networks

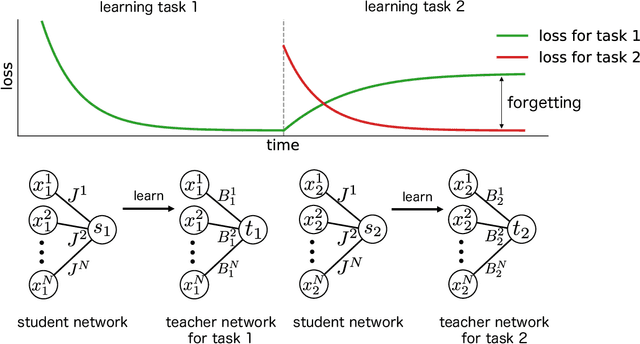
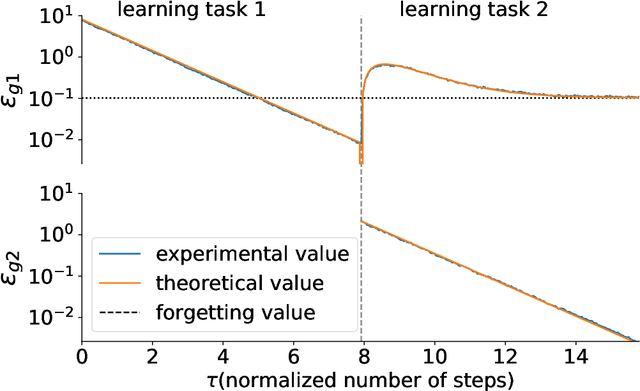
When a computational system continuously learns from an ever-changing environment, it rapidly forgets its past experiences. This phenomenon is called catastrophic forgetting. While a line of studies has been proposed with respect to avoiding catastrophic forgetting, most of the methods are based on intuitive insights into the phenomenon, and their performances have been evaluated by numerical experiments using benchmark datasets. Therefore, in this study, we provide the theoretical framework for analyzing catastrophic forgetting by using teacher-student learning. Teacher-student learning is a framework in which we introduce two neural networks: one neural network is a target function in supervised learning, and the other is a learning neural network. To analyze continual learning in the teacher-student framework, we introduce the similarity of the input distribution and the input-output relationship of the target functions as the similarity of tasks. In this theoretical framework, we also provide a qualitative understanding of how a single-layer linear learning neural network forgets tasks. Based on the analysis, we find that the network can avoid catastrophic forgetting when the similarity among input distributions is small and that of the input-output relationship of the target functions is large. The analysis also suggests that a system often exhibits a characteristic phenomenon called overshoot, which means that even if the learning network has once undergone catastrophic forgetting, it is possible that the network may perform reasonably well after further learning of the current task.

Exhaustive search for sparse variable selection in linear regression

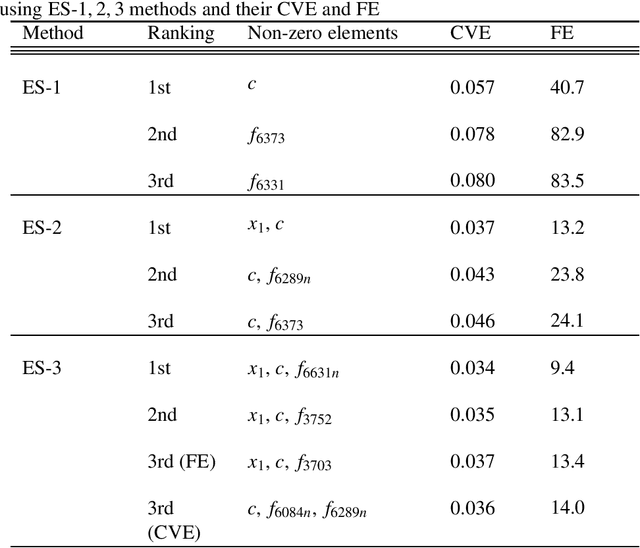
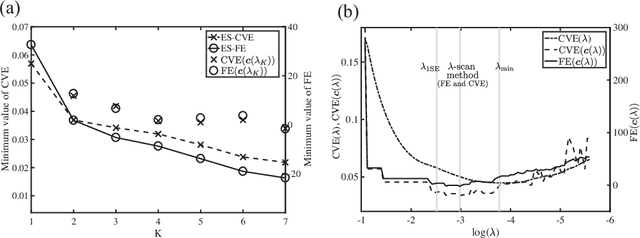
We propose a K-sparse exhaustive search (ES-K) method and a K-sparse approximate exhaustive search method (AES-K) for selecting variables in linear regression. With these methods, K-sparse combinations of variables are tested exhaustively assuming that the optimal combination of explanatory variables is K-sparse. By collecting the results of exhaustively computing ES-K, various approximate methods for selecting sparse variables can be summarized as density of states. With this density of states, we can compare different methods for selecting sparse variables such as relaxation and sampling. For large problems where the combinatorial explosion of explanatory variables is crucial, the AES-K method enables density of states to be effectively reconstructed by using the replica-exchange Monte Carlo method and the multiple histogram method. Applying the ES-K and AES-K methods to type Ia supernova data, we confirmed the conventional understanding in astronomy when an appropriate K is given beforehand. However, we found the difficulty to determine K from the data. Using virtual measurement and analysis, we argue that this is caused by data shortage.