Statistical Mechanical Analysis of Catastrophic Forgetting in Continual Learning with Teacher and Student Networks

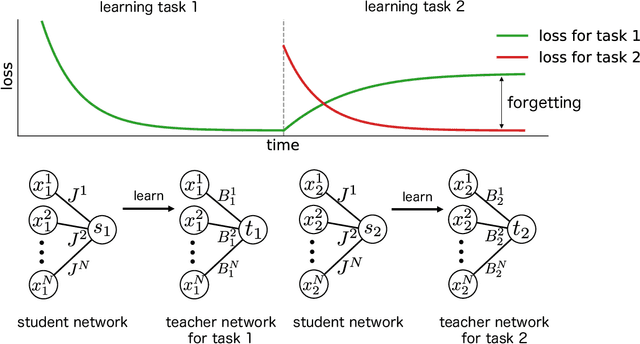
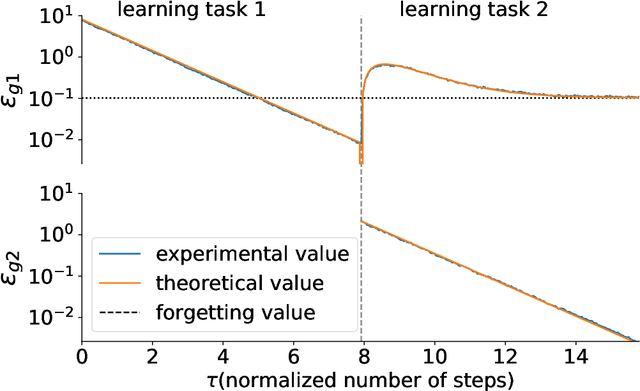
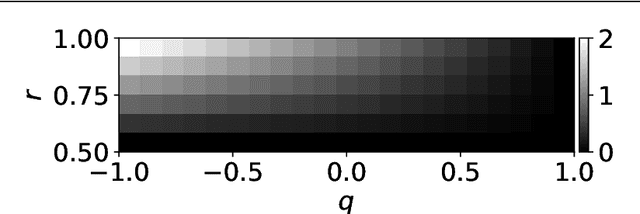
When a computational system continuously learns from an ever-changing environment, it rapidly forgets its past experiences. This phenomenon is called catastrophic forgetting. While a line of studies has been proposed with respect to avoiding catastrophic forgetting, most of the methods are based on intuitive insights into the phenomenon, and their performances have been evaluated by numerical experiments using benchmark datasets. Therefore, in this study, we provide the theoretical framework for analyzing catastrophic forgetting by using teacher-student learning. Teacher-student learning is a framework in which we introduce two neural networks: one neural network is a target function in supervised learning, and the other is a learning neural network. To analyze continual learning in the teacher-student framework, we introduce the similarity of the input distribution and the input-output relationship of the target functions as the similarity of tasks. In this theoretical framework, we also provide a qualitative understanding of how a single-layer linear learning neural network forgets tasks. Based on the analysis, we find that the network can avoid catastrophic forgetting when the similarity among input distributions is small and that of the input-output relationship of the target functions is large. The analysis also suggests that a system often exhibits a characteristic phenomenon called overshoot, which means that even if the learning network has once undergone catastrophic forgetting, it is possible that the network may perform reasonably well after further learning of the current task.

Data-Dependence of Plateau Phenomenon in Learning with Neural Network --- Statistical Mechanical Analysis

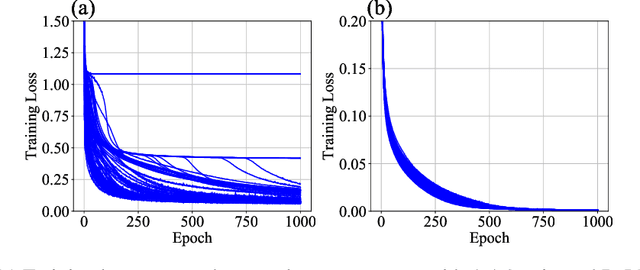
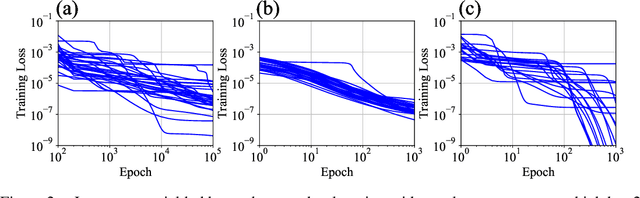
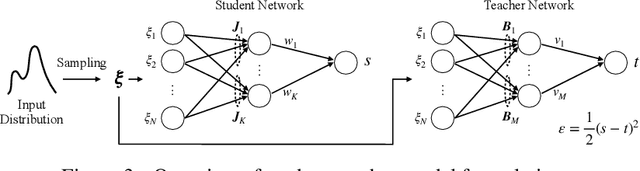
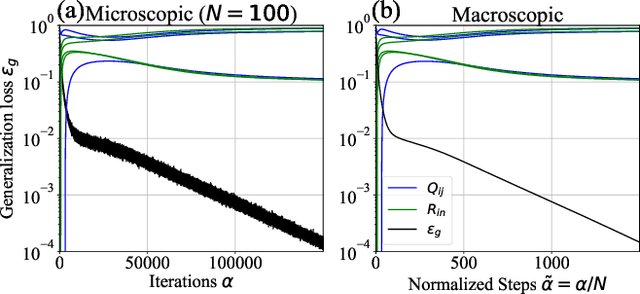
The plateau phenomenon, wherein the loss value stops decreasing during the process of learning, has been reported by various researchers. The phenomenon is actively inspected in the 1990s and found to be due to the fundamental hierarchical structure of neural network models. Then the phenomenon has been thought as inevitable. However, the phenomenon seldom occurs in the context of recent deep learning. There is a gap between theory and reality. In this paper, using statistical mechanical formulation, we clarified the relationship between the plateau phenomenon and the statistical property of the data learned. It is shown that the data whose covariance has small and dispersed eigenvalues tend to make the plateau phenomenon inconspicuous.

Saliency Fusion in Eigenvector Space with Multi-Channel Pulse Coupled Neural Network

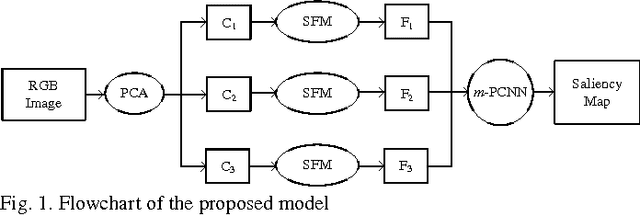
Saliency computation has become a popular research field for many applications due to the useful information provided by saliency maps. For a saliency map, local relations around the salient regions in multi-channel perspective should be taken into consideration by aiming uniformity on the region of interest as an internal approach. And, irrelevant salient regions have to be avoided as much as possible. Most of the works achieve these criteria with external processing modules; however, these can be accomplished during the conspicuity map fusion process. Therefore, in this paper, a new model is proposed for saliency/conspicuity map fusion with two concepts: a) input image transformation relying on the principal component analysis (PCA), and b) saliency conspicuity map fusion with multi-channel pulsed coupled neural network (m-PCNN). Experimental results, which are evaluated by precision, recall, F-measure, and area under curve (AUC), support the reliability of the proposed method by enhancing the saliency computation.