Data-Dependence of Plateau Phenomenon in Learning with Neural Network --- Statistical Mechanical Analysis
Paper and Code
Jan 10, 2020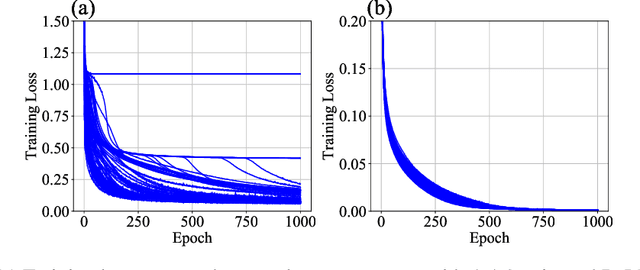
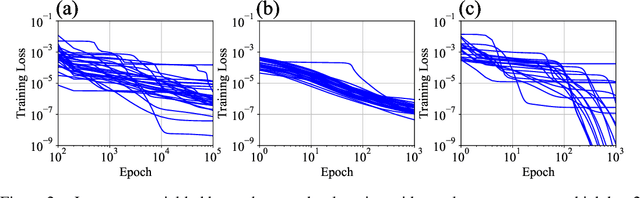
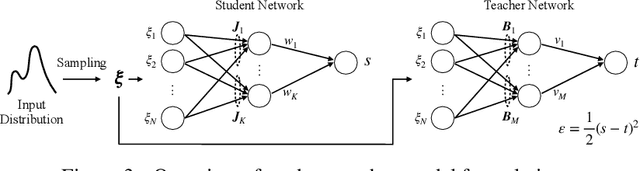
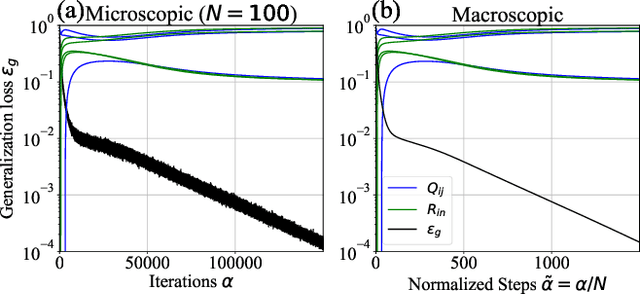
The plateau phenomenon, wherein the loss value stops decreasing during the process of learning, has been reported by various researchers. The phenomenon is actively inspected in the 1990s and found to be due to the fundamental hierarchical structure of neural network models. Then the phenomenon has been thought as inevitable. However, the phenomenon seldom occurs in the context of recent deep learning. There is a gap between theory and reality. In this paper, using statistical mechanical formulation, we clarified the relationship between the plateau phenomenon and the statistical property of the data learned. It is shown that the data whose covariance has small and dispersed eigenvalues tend to make the plateau phenomenon inconspicuous.
* Accepted at NeurIPS 2019
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge