Sharp Learning Bounds for Contrastive Unsupervised Representation Learning

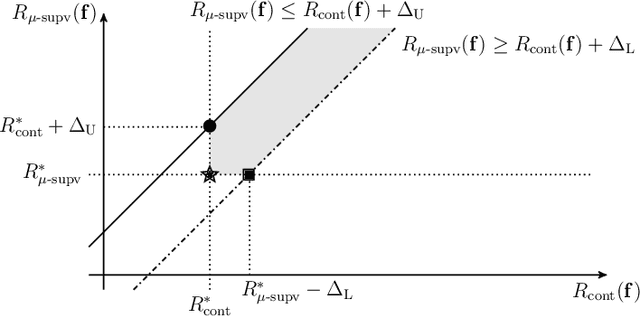
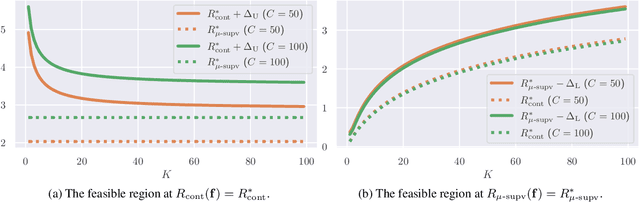
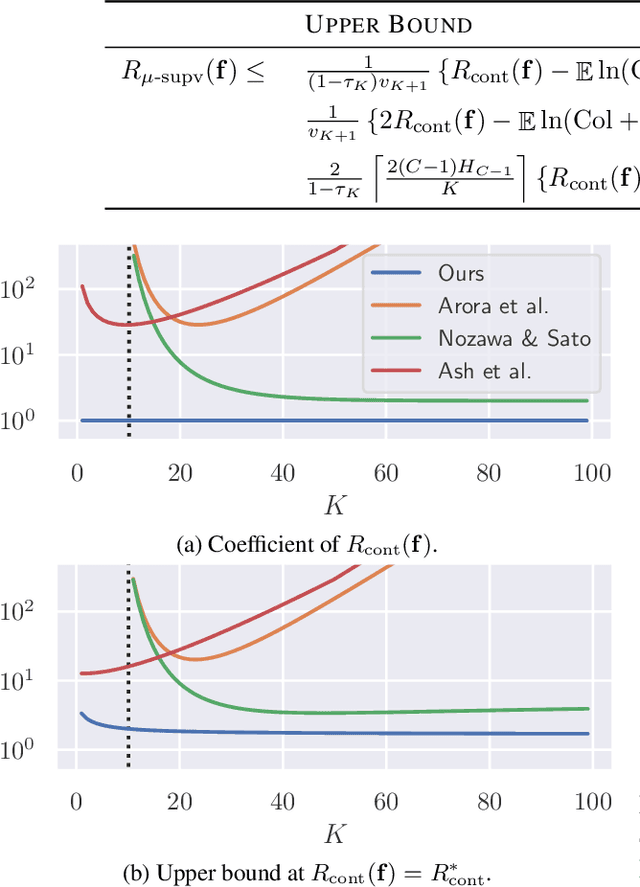
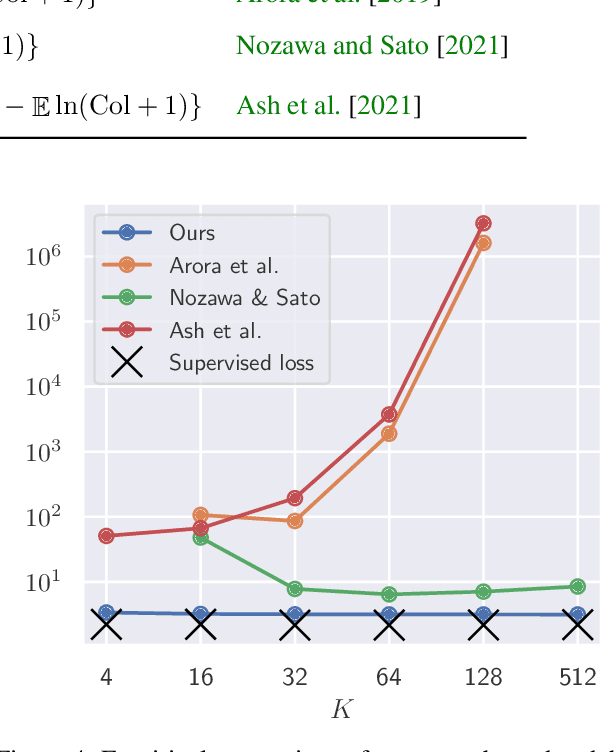
Contrastive unsupervised representation learning (CURL) encourages data representation to make semantically similar pairs closer than randomly drawn negative samples, which has been successful in various domains such as vision, language, and graphs. Although recent theoretical studies have attempted to explain its success by upper bounds of a downstream classification loss by the contrastive loss, they are still not sharp enough to explain an experimental fact: larger negative samples improve the classification performance. This study establishes a downstream classification loss bound with a tight intercept in the negative sample size. By regarding the contrastive loss as a downstream loss estimator, our theory not only improves the existing learning bounds substantially but also explains why downstream classification empirically improves with larger negative samples -- because the estimation variance of the downstream loss decays with larger negative samples. We verify that our theory is consistent with experiments on synthetic, vision, and language datasets.

Statistical Mechanical Analysis of Catastrophic Forgetting in Continual Learning with Teacher and Student Networks

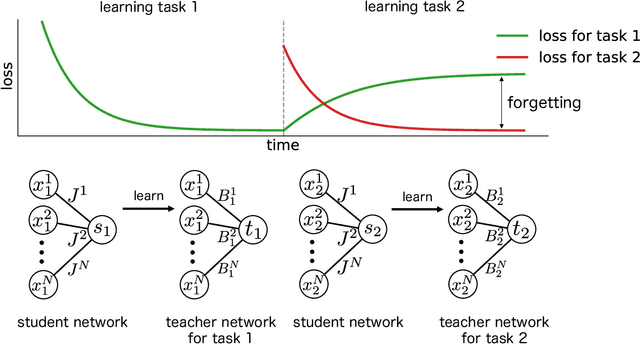
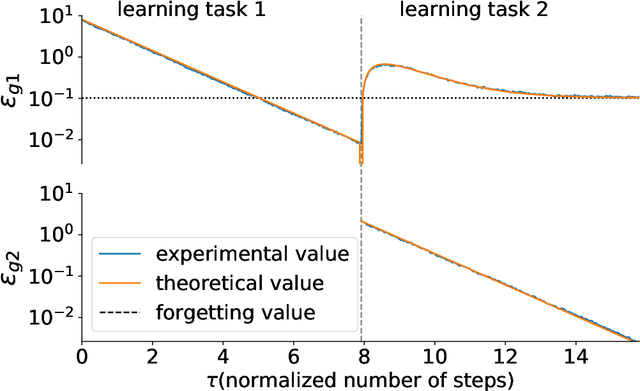
When a computational system continuously learns from an ever-changing environment, it rapidly forgets its past experiences. This phenomenon is called catastrophic forgetting. While a line of studies has been proposed with respect to avoiding catastrophic forgetting, most of the methods are based on intuitive insights into the phenomenon, and their performances have been evaluated by numerical experiments using benchmark datasets. Therefore, in this study, we provide the theoretical framework for analyzing catastrophic forgetting by using teacher-student learning. Teacher-student learning is a framework in which we introduce two neural networks: one neural network is a target function in supervised learning, and the other is a learning neural network. To analyze continual learning in the teacher-student framework, we introduce the similarity of the input distribution and the input-output relationship of the target functions as the similarity of tasks. In this theoretical framework, we also provide a qualitative understanding of how a single-layer linear learning neural network forgets tasks. Based on the analysis, we find that the network can avoid catastrophic forgetting when the similarity among input distributions is small and that of the input-output relationship of the target functions is large. The analysis also suggests that a system often exhibits a characteristic phenomenon called overshoot, which means that even if the learning network has once undergone catastrophic forgetting, it is possible that the network may perform reasonably well after further learning of the current task.

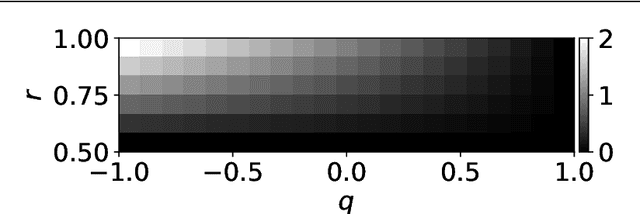
A Differentiable Gaussian-like Distribution on Hyperbolic Space for Gradient-Based Learning

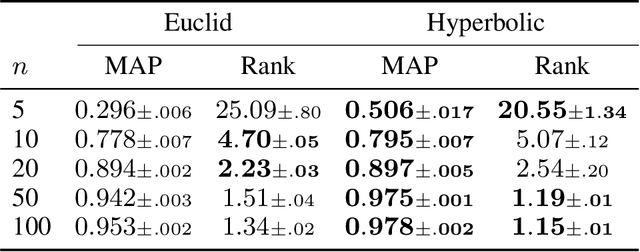
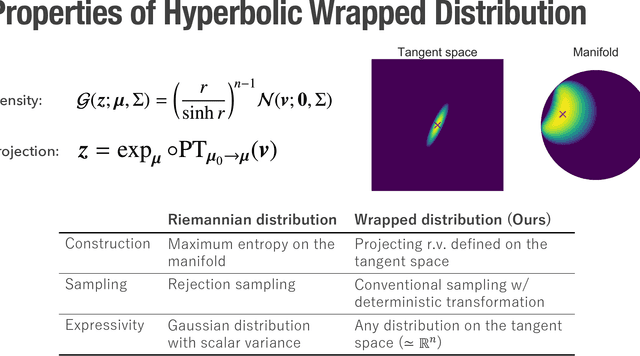
Hyperbolic space is a geometry that is known to be well-suited for representation learning of data with an underlying hierarchical structure. In this paper, we present a novel hyperbolic distribution called \textit{pseudo-hyperbolic Gaussian}, a Gaussian-like distribution on hyperbolic space whose density can be evaluated analytically and differentiated with respect to the parameters. Our distribution enables the gradient-based learning of the probabilistic models on hyperbolic space that could never have been considered before. Also, we can sample from this hyperbolic probability distribution without resorting to auxiliary means like rejection sampling. As applications of our distribution, we develop a hyperbolic-analog of variational autoencoder and a method of probabilistic word embedding on hyperbolic space. We demonstrate the efficacy of our distribution on various datasets including MNIST, Atari 2600 Breakout, and WordNet.

Concept Formation and Dynamics of Repeated Inference in Deep Generative Models

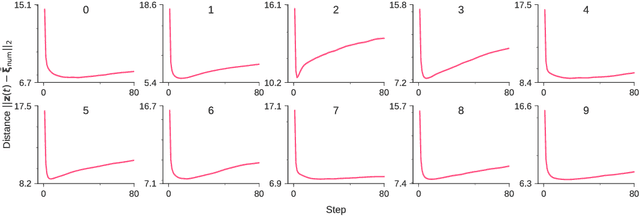
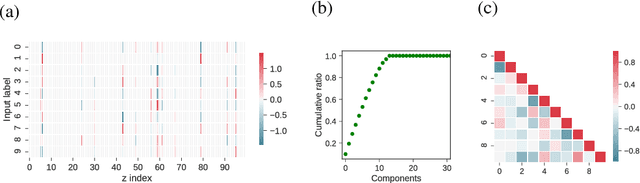
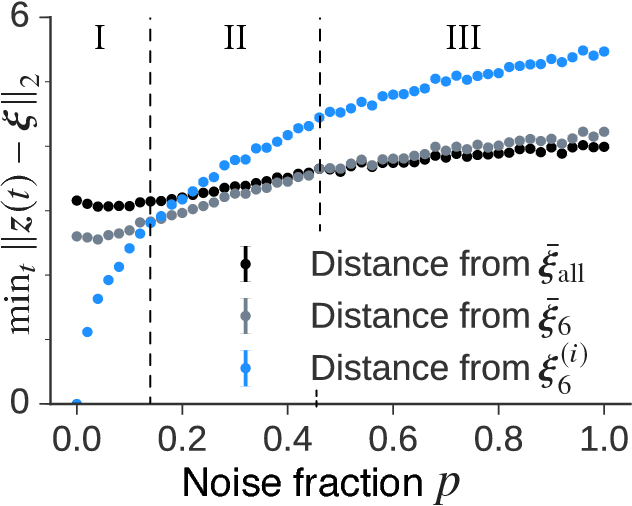
Deep generative models are reported to be useful in broad applications including image generation. Repeated inference between data space and latent space in these models can denoise cluttered images and improve the quality of inferred results. However, previous studies only qualitatively evaluated image outputs in data space, and the mechanism behind the inference has not been investigated. The purpose of the current study is to numerically analyze changes in activity patterns of neurons in the latent space of a deep generative model called a "variational auto-encoder" (VAE). What kinds of inference dynamics the VAE demonstrates when noise is added to the input data are identified. The VAE embeds a dataset with clear cluster structures in the latent space and the center of each cluster of multiple correlated data points (memories) is referred as the concept. Our study demonstrated that transient dynamics of inference first approaches a concept, and then moves close to a memory. Moreover, the VAE revealed that the inference dynamics approaches a more abstract concept to the extent that the uncertainty of input data increases due to noise. It was demonstrated that by increasing the number of the latent variables, the trend of the inference dynamics to approach a concept can be enhanced, and the generalization ability of the VAE can be improved.