Masanori Koyama
Simultaneous Learning of Optimal Transports for Training All-to-All Flow-Based Condition Transfer Model
Apr 04, 2025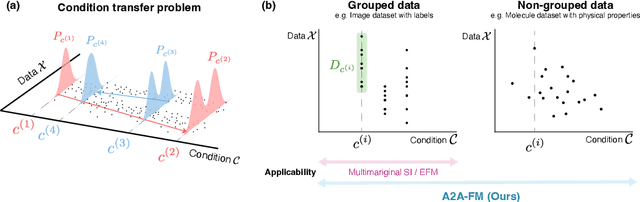

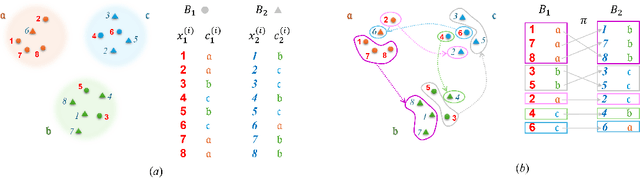

Abstract:In this paper, we propose a flow-based method for learning all-to-all transfer maps among conditional distributions, approximating pairwise optimal transport. The proposed method addresses the challenge of handling continuous conditions, which often involve a large set of conditions with sparse empirical observations per condition. We introduce a novel cost function that enables simultaneous learning of optimal transports for all pairs of conditional distributions. Our method is supported by a theoretical guarantee that, in the limit, it converges to pairwise optimal transports among infinite pairs of conditional distributions. The learned transport maps are subsequently used to couple data points in conditional flow matching. We demonstrate the effectiveness of this method on synthetic and benchmark datasets, as well as on chemical datasets where continuous physical properties are defined as conditions.
Inter-environmental world modeling for continuous and compositional dynamics
Mar 13, 2025Abstract:Various world model frameworks are being developed today based on autoregressive frameworks that rely on discrete representations of actions and observations, and these frameworks are succeeding in constructing interactive generative models for the target environment of interest. Meanwhile, humans demonstrate remarkable generalization abilities to combine experiences in multiple environments to mentally simulate and learn to control agents in diverse environments. Inspired by this human capability, we introduce World modeling through Lie Action (WLA), an unsupervised framework that learns continuous latent action representations to simulate across environments. WLA learns a control interface with high controllability and predictive ability by simultaneously modeling the dynamics of multiple environments using Lie group theory and object-centric autoencoder. On synthetic benchmark and real-world datasets, we demonstrate that WLA can be trained using only video frames and, with minimal or no action labels, can quickly adapt to new environments with novel action sets.
Flow matching achieves minimax optimal convergence
May 31, 2024Abstract:Flow matching (FM) has gained significant attention as a simulation-free generative model. Unlike diffusion models, which are based on stochastic differential equations, FM employs a simpler approach by solving an ordinary differential equation with an initial condition from a normal distribution, thus streamlining the sample generation process. This paper discusses the convergence properties of FM in terms of the $p$-Wasserstein distance, a measure of distributional discrepancy. We establish that FM can achieve the minmax optimal convergence rate for $1 \leq p \leq 2$, presenting the first theoretical evidence that FM can reach convergence rates comparable to those of diffusion models. Our analysis extends existing frameworks by examining a broader class of mean and variance functions for the vector fields and identifies specific conditions necessary to attain these optimal rates.
Extended Flow Matching: a Method of Conditional Generation with Generalized Continuity Equation
Mar 03, 2024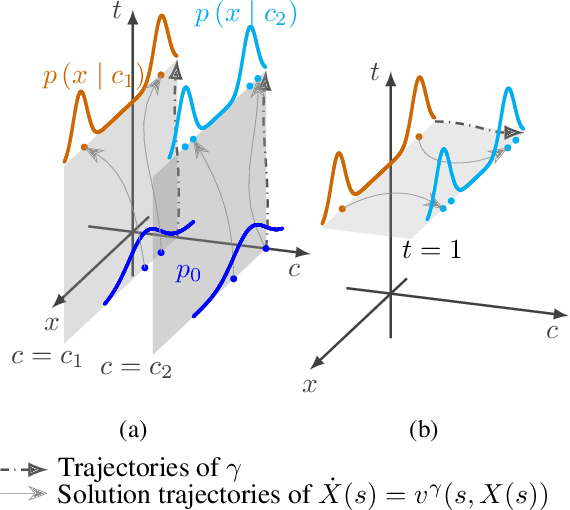
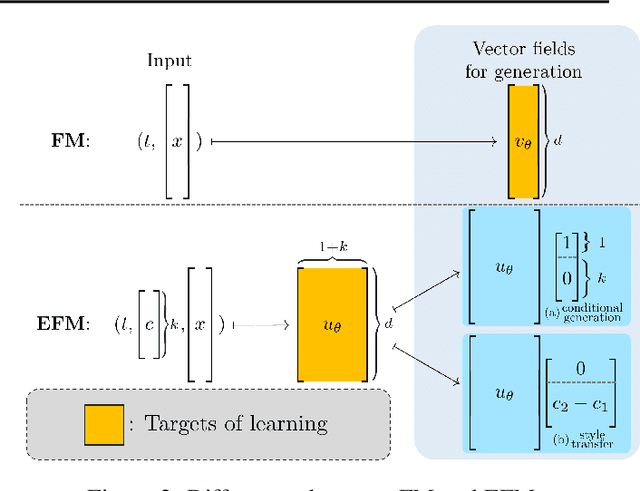
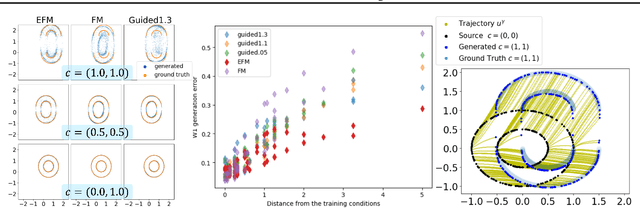
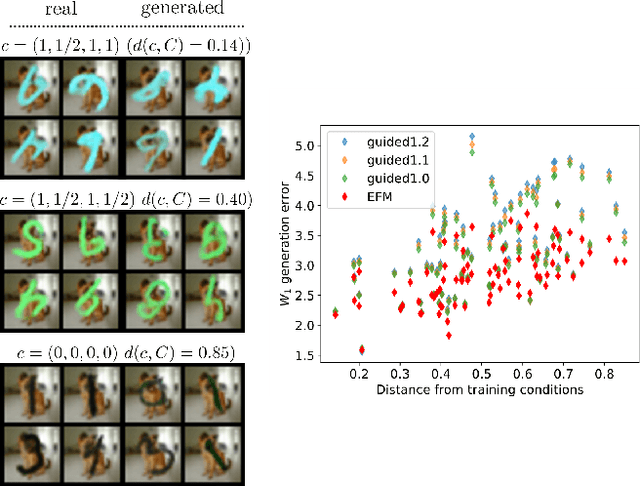
Abstract:The task of conditional generation is one of the most important applications of generative models, and numerous methods have been developed to date based on the celebrated diffusion models, with the guidance-based classifier-free method taking the lead. However, the theory of the guidance-based method not only requires the user to fine-tune the "guidance strength," but its target vector field does not necessarily correspond to the conditional distribution used in training. In this paper, we develop the theory of conditional generation based on Flow Matching, a current strong contender of diffusion methods. Motivated by the interpretation of a probability path as a distribution on path space, we establish a novel theory of flow-based generation of conditional distribution by employing the mathematical framework of generalized continuity equation instead of the continuity equation in flow matching. This theory naturally derives a method that aims to match the matrix field as opposed to the vector field. Our framework ensures the continuity of the generated conditional distribution through the existence of flow between conditional distributions. We will present our theory through experiments and mathematical results.
Neural Fourier Transform: A General Approach to Equivariant Representation Learning
May 29, 2023
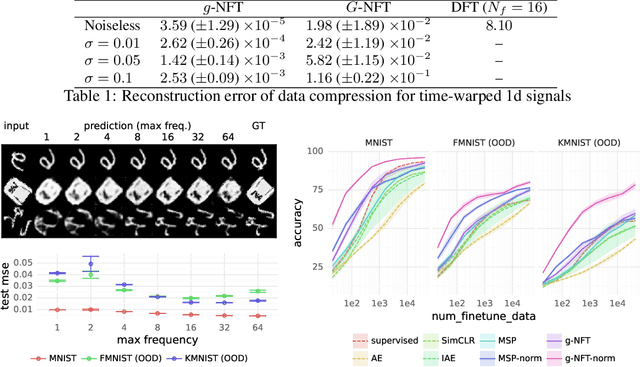
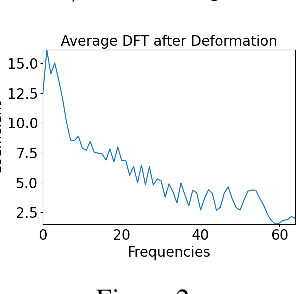

Abstract:Symmetry learning has proven to be an effective approach for extracting the hidden structure of data, with the concept of equivariance relation playing the central role. However, most of the current studies are built on architectural theory and corresponding assumptions on the form of data. We propose Neural Fourier Transform (NFT), a general framework of learning the latent linear action of the group without assuming explicit knowledge of how the group acts on data. We present the theoretical foundations of NFT and show that the existence of a linear equivariant feature, which has been assumed ubiquitously in equivariance learning, is equivalent to the existence of a group invariant kernel on the dataspace. We also provide experimental results to demonstrate the application of NFT in typical scenarios with varying levels of knowledge about the acting group.
Invariance-adapted decomposition and Lasso-type contrastive learning
Oct 13, 2022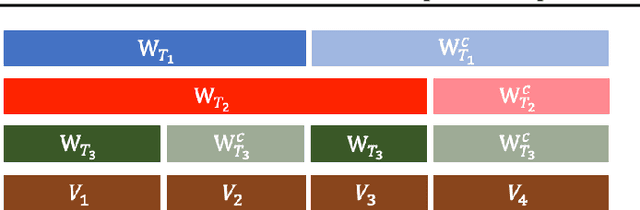


Abstract:Recent years have witnessed the effectiveness of contrastive learning in obtaining the representation of dataset that is useful in interpretation and downstream tasks. However, the mechanism that describes this effectiveness have not been thoroughly analyzed, and many studies have been conducted to investigate the data structures captured by contrastive learning. In particular, the recent study of \citet{content_isolate} has shown that contrastive learning is capable of decomposing the data space into the space that is invariant to all augmentations and its complement. In this paper, we introduce the notion of invariance-adapted latent space that decomposes the data space into the intersections of the invariant spaces of each augmentation and their complements. This decomposition generalizes the one introduced in \citet{content_isolate}, and describes a structure that is analogous to the frequencies in the harmonic analysis of a group. We experimentally show that contrastive learning with lasso-type metric can be used to find an invariance-adapted latent space, thereby suggesting a new potential for the contrastive learning. We also investigate when such a latent space can be identified up to mixings within each component.
Unsupervised Learning of Equivariant Structure from Sequences
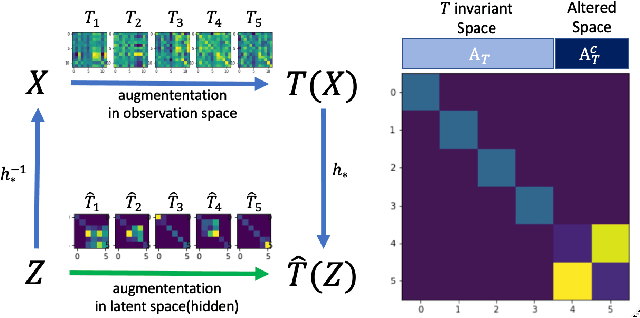
Oct 12, 2022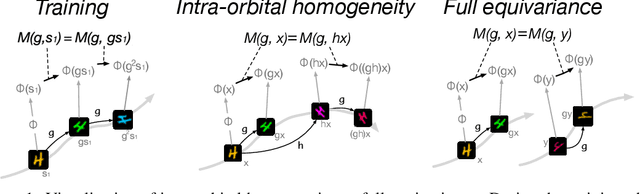

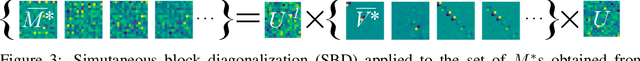
Abstract:In this study, we present meta-sequential prediction (MSP), an unsupervised framework to learn the symmetry from the time sequence of length at least three. Our method leverages the stationary property (e.g. constant velocity, constant acceleration) of the time sequence to learn the underlying equivariant structure of the dataset by simply training the encoder-decoder model to be able to predict the future observations. We will demonstrate that, with our framework, the hidden disentangled structure of the dataset naturally emerges as a by-product by applying simultaneous block-diagonalization to the transition operators in the latent space, the procedure which is commonly used in representation theory to decompose the feature-space based on the type of response to group actions. We will showcase our method from both empirical and theoretical perspectives. Our result suggests that finding a simple structured relation and learning a model with extrapolation capability are two sides of the same coin. The code is available at https://github.com/takerum/meta_sequential_prediction.
Contrastive Representation Learning with Trainable Augmentation Channel
Nov 15, 2021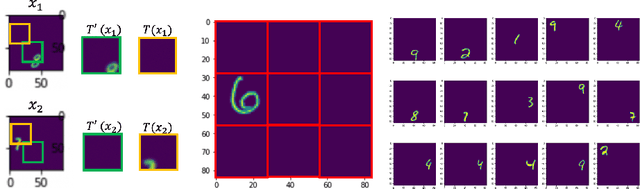

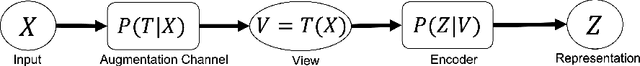

Abstract:In contrastive representation learning, data representation is trained so that it can classify the image instances even when the images are altered by augmentations. However, depending on the datasets, some augmentations can damage the information of the images beyond recognition, and such augmentations can result in collapsed representations. We present a partial solution to this problem by formalizing a stochastic encoding process in which there exist a tug-of-war between the data corruption introduced by the augmentations and the information preserved by the encoder. We show that, with the infoMax objective based on this framework, we can learn a data-dependent distribution of augmentations to avoid the collapse of the representation.
Out-of-Distribution Generalization with Maximal Invariant Predictor
Aug 04, 2020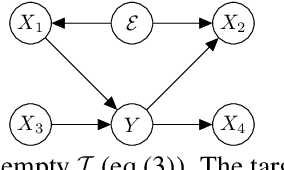


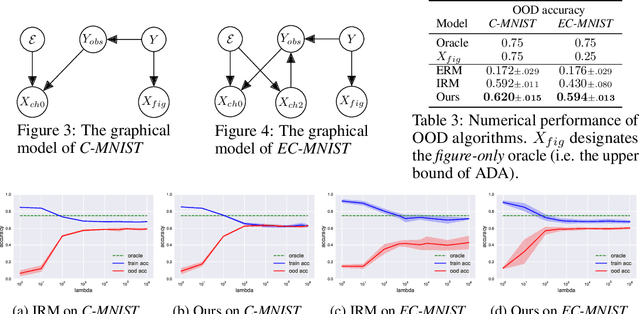
Abstract:Out-of-Distribution (OOD) generalization problem is a problem of seeking the predictor function whose performance in the worst environments is optimal. This paper makes two contributions to OOD problem. We first use the basic results of probability to prove maximal Invariant Predictor(MIP) condition, a theoretical result that can be used to identify the OOD optimal solution. We then use our MIP to derive inner-environmental Gradient Alignment(IGA) algorithm that can be used to help seek the OOD optimal predictor. Previous studies that have investigated the theoretical aspect of the OOD-problem use strong structural assumptions such as causal DAG. However, in cases involving image datasets, for example, the identification of hidden structural relations is itself a difficult problem. Our theoretical results are different from those of many previous studies in that it can be applied to cases in which the underlying structure of a dataset is difficult to analyze. We present an extensive comparison of previous theoretical approaches to the OODproblems based on the assumptions they make. We also present an extension of the colored-MNIST that can more accurately represent the pathological OOD situation than the original version, and demonstrate the superiority of IGA over previous methods on both the original and the extended version of Colored-MNIST.
Learning Structured Latent Factors from Dependent Data:A Generative Model Framework from Information-Theoretic Perspective
Jul 21, 2020
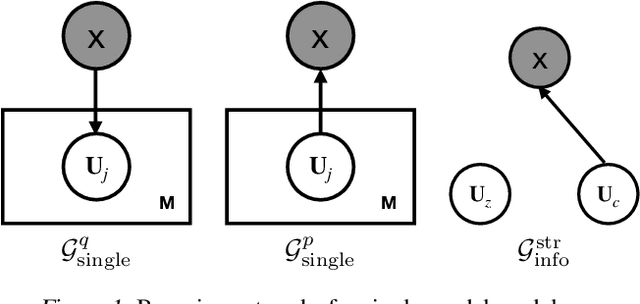
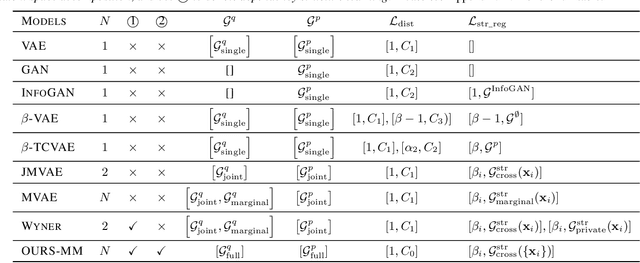
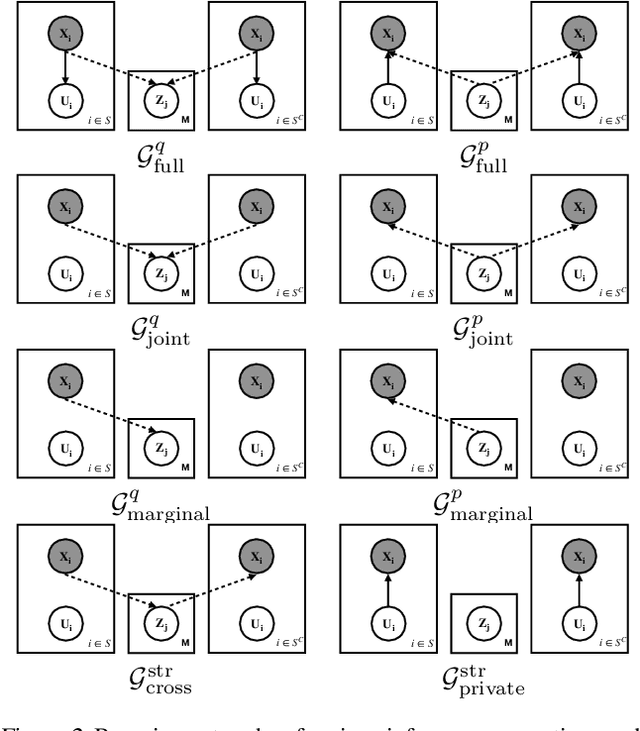
Abstract:Learning controllable and generalizable representation of multivariate data with desired structural properties remains a fundamental problem in machine learning. In this paper, we present a novel framework for learning generative models with various underlying structures in the latent space. We represent the inductive bias in the form of mask variables to model the dependency structure in the graphical model and extend the theory of multivariate information bottleneck to enforce it. Our model provides a principled approach to learn a set of semantically meaningful latent factors that reflect various types of desired structures like capturing correlation or encoding invariance, while also offering the flexibility to automatically estimate the dependency structure from data. We show that our framework unifies many existing generative models and can be applied to a variety of tasks including multi-modal data modeling, algorithmic fairness, and invariant risk minimization.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge