Error Analysis of Option Pricing via Deep PDE Solvers: Empirical Study

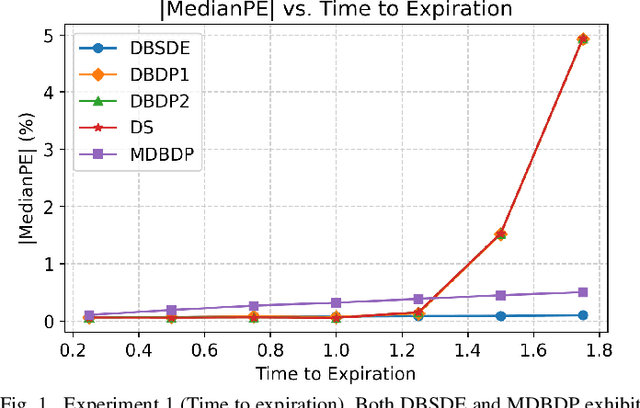
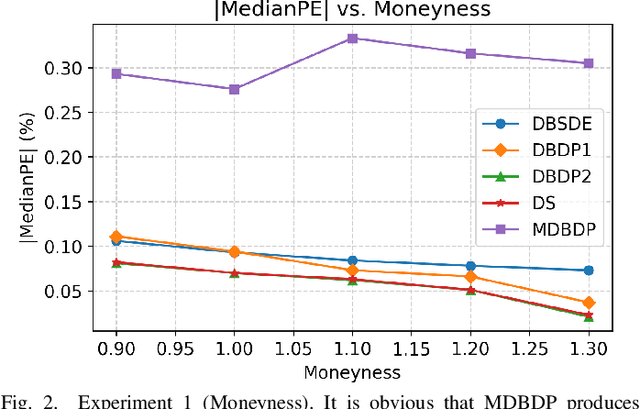
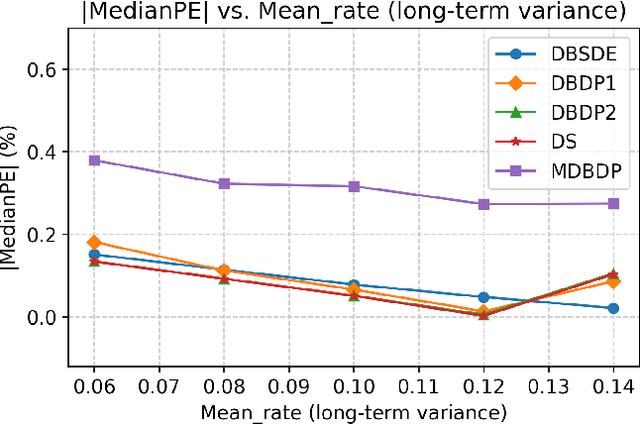
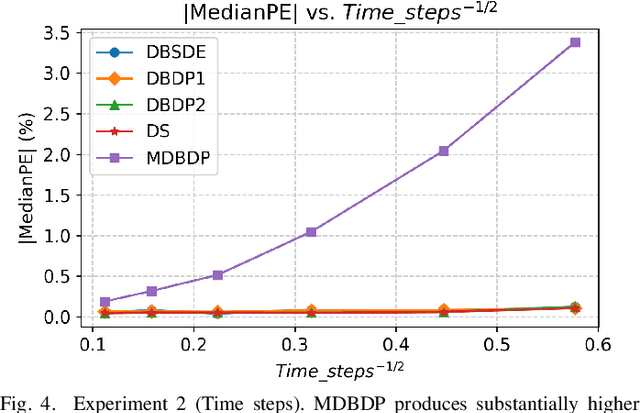
Option pricing, a fundamental problem in finance, often requires solving non-linear partial differential equations (PDEs). When dealing with multi-asset options, such as rainbow options, these PDEs become high-dimensional, leading to challenges posed by the curse of dimensionality. While deep learning-based PDE solvers have recently emerged as scalable solutions to this high-dimensional problem, their empirical and quantitative accuracy remains not well-understood, hindering their real-world applicability. In this study, we aimed to offer actionable insights into the utility of Deep PDE solvers for practical option pricing implementation. Through comparative experiments, we assessed the empirical performance of these solvers in high-dimensional contexts. Our investigation identified three primary sources of errors in Deep PDE solvers: (i) errors inherent in the specifications of the target option and underlying assets, (ii) errors originating from the asset model simulation methods, and (iii) errors stemming from the neural network training. Through ablation studies, we evaluated the individual impact of each error source. Our results indicate that the Deep BSDE method (DBSDE) is superior in performance and exhibits robustness against variations in option specifications. In contrast, some other methods are overly sensitive to option specifications, such as time to expiration. We also find that the performance of these methods improves inversely proportional to the square root of batch size and the number of time steps. This observation can aid in estimating computational resources for achieving desired accuracies with Deep PDE solvers.

Adversarial Deep Hedging: Learning to Hedge without Price Process Modeling

Deep hedging is a deep-learning-based framework for derivative hedging in incomplete markets. The advantage of deep hedging lies in its ability to handle various realistic market conditions, such as market frictions, which are challenging to address within the traditional mathematical finance framework. Since deep hedging relies on market simulation, the underlying asset price process model is crucial. However, existing literature on deep hedging often relies on traditional mathematical finance models, e.g., Brownian motion and stochastic volatility models, and discovering effective underlying asset models for deep hedging learning has been a challenge. In this study, we propose a new framework called adversarial deep hedging, inspired by adversarial learning. In this framework, a hedger and a generator, which respectively model the underlying asset process and the underlying asset process, are trained in an adversarial manner. The proposed method enables to learn a robust hedger without explicitly modeling the underlying asset process. Through numerical experiments, we demonstrate that our proposed method achieves competitive performance to models that assume explicit underlying asset processes across various real market data.

Uncertainty Aware Trader-Company Method: Interpretable Stock Price Prediction Capturing Uncertainty

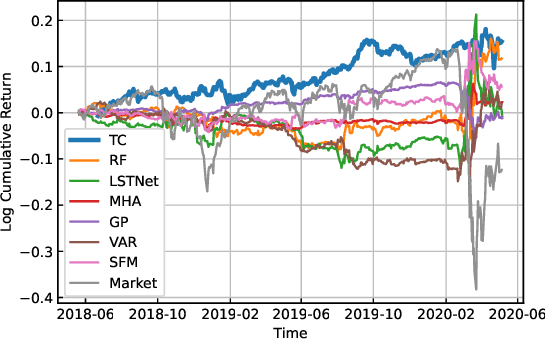
Machine learning is an increasingly popular tool with some success in predicting stock prices. One promising method is the Trader-Company~(TC) method, which takes into account the dynamism of the stock market and has both high predictive power and interpretability. Machine learning-based stock prediction methods including the TC method have been concentrating on point prediction. However, point prediction in the absence of uncertainty estimates lacks credibility quantification and raises concerns about safety. The challenge in this paper is to make an investment strategy that combines high predictive power and the ability to quantify uncertainty. We propose a novel approach called Uncertainty Aware Trader-Company Method~(UTC) method. The core idea of this approach is to combine the strengths of both frameworks by merging the TC method with the probabilistic modeling, which provides probabilistic predictions and uncertainty estimations. We expect this to retain the predictive power and interpretability of the TC method while capturing the uncertainty. We theoretically prove that the proposed method estimates the posterior variance and does not introduce additional biases from the original TC method. We conduct a comprehensive evaluation of our approach based on the synthetic and real market datasets. We confirm with synthetic data that the UTC method can detect situations where the uncertainty increases and the prediction is difficult. We also confirmed that the UTC method can detect abrupt changes in data generating distributions. We demonstrate with real market data that the UTC method can achieve higher returns and lower risks than baselines.

Unified Perspective on Probability Divergence via Maximum Likelihood Density Ratio Estimation: Bridging KL-Divergence and Integral Probability Metrics

This paper provides a unified perspective for the Kullback-Leibler (KL)-divergence and the integral probability metrics (IPMs) from the perspective of maximum likelihood density-ratio estimation (DRE). Both the KL-divergence and the IPMs are widely used in various fields in applications such as generative modeling. However, a unified understanding of these concepts has still been unexplored. In this paper, we show that the KL-divergence and the IPMs can be represented as maximal likelihoods differing only by sampling schemes, and use this result to derive a unified form of the IPMs and a relaxed estimation method. To develop the estimation problem, we construct an unconstrained maximum likelihood estimator to perform DRE with a stratified sampling scheme. We further propose a novel class of probability divergences, called the Density Ratio Metrics (DRMs), that interpolates the KL-divergence and the IPMs. In addition to these findings, we also introduce some applications of the DRMs, such as DRE and generative adversarial networks. In experiments, we validate the effectiveness of our proposed methods.

Contrastive Representation Learning with Trainable Augmentation Channel

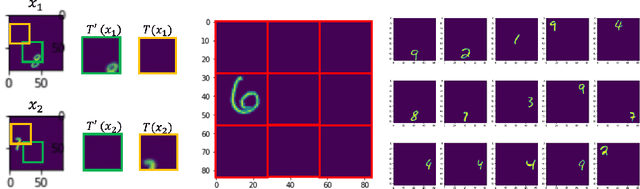
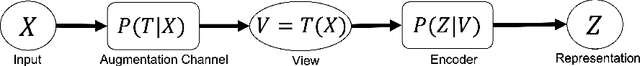
In contrastive representation learning, data representation is trained so that it can classify the image instances even when the images are altered by augmentations. However, depending on the datasets, some augmentations can damage the information of the images beyond recognition, and such augmentations can result in collapsed representations. We present a partial solution to this problem by formalizing a stochastic encoding process in which there exist a tug-of-war between the data corruption introduced by the augmentations and the information preserved by the encoder. We show that, with the infoMax objective based on this framework, we can learn a data-dependent distribution of augmentations to avoid the collapse of the representation.

What Data Augmentation Do We Need for Deep-Learning-Based Finance?

The main task we consider is portfolio construction in a speculative market, a fundamental problem in modern finance. While various empirical works now exist to explore deep learning in finance, the theory side is almost non-existent. In this work, we focus on developing a theoretical framework for understanding the use of data augmentation for deep-learning-based approaches to quantitative finance. The proposed theory clarifies the role and necessity of data augmentation for finance; moreover, our theory motivates a simple algorithm of injecting a random noise of strength $\sqrt{|r_{t-1}|}$ to the observed return $r_{t}$. This algorithm is shown to work well in practice.

Trader-Company Method: A Metaheuristic for Interpretable Stock Price Prediction

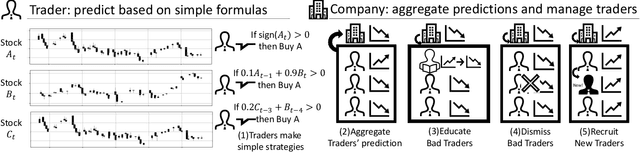
Investors try to predict returns of financial assets to make successful investment. Many quantitative analysts have used machine learning-based methods to find unknown profitable market rules from large amounts of market data. However, there are several challenges in financial markets hindering practical applications of machine learning-based models. First, in financial markets, there is no single model that can consistently make accurate prediction because traders in markets quickly adapt to newly available information. Instead, there are a number of ephemeral and partially correct models called "alpha factors". Second, since financial markets are highly uncertain, ensuring interpretability of prediction models is quite important to make reliable trading strategies. To overcome these challenges, we propose the Trader-Company method, a novel evolutionary model that mimics the roles of a financial institute and traders belonging to it. Our method predicts future stock returns by aggregating suggestions from multiple weak learners called Traders. A Trader holds a collection of simple mathematical formulae, each of which represents a candidate of an alpha factor and would be interpretable for real-world investors. The aggregation algorithm, called a Company, maintains multiple Traders. By randomly generating new Traders and retraining them, Companies can efficiently find financially meaningful formulae whilst avoiding overfitting to a transient state of the market. We show the effectiveness of our method by conducting experiments on real market data.

Deep Portfolio Optimization via Distributional Prediction of Residual Factors

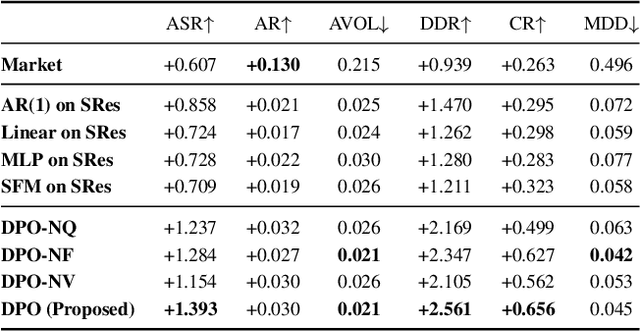
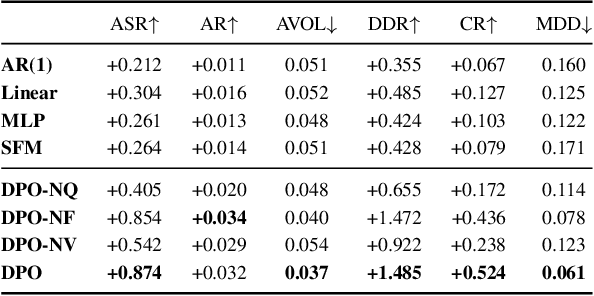
Recent developments in deep learning techniques have motivated intensive research in machine learning-aided stock trading strategies. However, since the financial market has a highly non-stationary nature hindering the application of typical data-hungry machine learning methods, leveraging financial inductive biases is important to ensure better sample efficiency and robustness. In this study, we propose a novel method of constructing a portfolio based on predicting the distribution of a financial quantity called residual factors, which is known to be generally useful for hedging the risk exposure to common market factors. The key technical ingredients are twofold. First, we introduce a computationally efficient extraction method for the residual information, which can be easily combined with various prediction algorithms. Second, we propose a novel neural network architecture that allows us to incorporate widely acknowledged financial inductive biases such as amplitude invariance and time-scale invariance. We demonstrate the efficacy of our method on U.S. and Japanese stock market data. Through ablation experiments, we also verify that each individual technique contributes to improving the performance of trading strategies. We anticipate our techniques may have wide applications in various financial problems.

The equivalence between Stein variational gradient descent and black-box variational inference

We formalize an equivalence between two popular methods for Bayesian inference: Stein variational gradient descent (SVGD) and black-box variational inference (BBVI). In particular, we show that BBVI corresponds precisely to SVGD when the kernel is the neural tangent kernel. Furthermore, we interpret SVGD and BBVI as kernel gradient flows; we do this by leveraging the recent perspective that views SVGD as a gradient flow in the space of probability distributions and showing that BBVI naturally motivates a Riemannian structure on that space. We observe that kernel gradient flow also describes dynamics found in the training of generative adversarial networks (GANs). This work thereby unifies several existing techniques in variational inference and generative modeling and identifies the kernel as a fundamental object governing the behavior of these algorithms, motivating deeper analysis of its properties.

Smoothness and Stability in GANs

Generative adversarial networks, or GANs, commonly display unstable behavior during training. In this work, we develop a principled theoretical framework for understanding the stability of various types of GANs. In particular, we derive conditions that guarantee eventual stationarity of the generator when it is trained with gradient descent, conditions that must be satisfied by the divergence that is minimized by the GAN and the generator's architecture. We find that existing GAN variants satisfy some, but not all, of these conditions. Using tools from convex analysis, optimal transport, and reproducing kernels, we construct a GAN that fulfills these conditions simultaneously. In the process, we explain and clarify the need for various existing GAN stabilization techniques, including Lipschitz constraints, gradient penalties, and smooth activation functions.