CFTM: Continuous time fractional topic model

In this paper, we propose the Continuous Time Fractional Topic Model (cFTM), a new method for dynamic topic modeling. This approach incorporates fractional Brownian motion~(fBm) to effectively identify positive or negative correlations in topic and word distribution over time, revealing long-term dependency or roughness. Our theoretical analysis shows that the cFTM can capture these long-term dependency or roughness in both topic and word distributions, mirroring the main characteristics of fBm. Moreover, we prove that the parameter estimation process for the cFTM is on par with that of LDA, traditional topic models. To demonstrate the cFTM's property, we conduct empirical study using economic news articles. The results from these tests support the model's ability to identify and track long-term dependency or roughness in topics over time.

Uncertainty Aware Trader-Company Method: Interpretable Stock Price Prediction Capturing Uncertainty

Machine learning is an increasingly popular tool with some success in predicting stock prices. One promising method is the Trader-Company~(TC) method, which takes into account the dynamism of the stock market and has both high predictive power and interpretability. Machine learning-based stock prediction methods including the TC method have been concentrating on point prediction. However, point prediction in the absence of uncertainty estimates lacks credibility quantification and raises concerns about safety. The challenge in this paper is to make an investment strategy that combines high predictive power and the ability to quantify uncertainty. We propose a novel approach called Uncertainty Aware Trader-Company Method~(UTC) method. The core idea of this approach is to combine the strengths of both frameworks by merging the TC method with the probabilistic modeling, which provides probabilistic predictions and uncertainty estimations. We expect this to retain the predictive power and interpretability of the TC method while capturing the uncertainty. We theoretically prove that the proposed method estimates the posterior variance and does not introduce additional biases from the original TC method. We conduct a comprehensive evaluation of our approach based on the synthetic and real market datasets. We confirm with synthetic data that the UTC method can detect situations where the uncertainty increases and the prediction is difficult. We also confirmed that the UTC method can detect abrupt changes in data generating distributions. We demonstrate with real market data that the UTC method can achieve higher returns and lower risks than baselines.

Fractional SDE-Net: Generation of Time Series Data with Long-term Memory

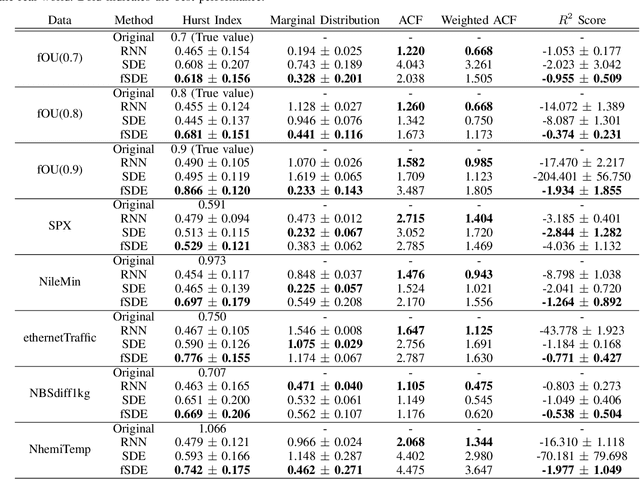
In this paper, we focus on generation of time-series data using neural networks. It is often the case that input time-series data, especially taken from real financial markets, is irregularly sampled, and its noise structure is more complicated than i.i.d. type. To generate time series with such a property, we propose fSDE-Net: neural fractional Stochastic Differential Equation Network. It generalizes the neural SDE model by using fractional Brownian motion with Hurst index larger than half, which exhibits long-term memory property. We derive the solver of fSDE-Net and theoretically analyze the existence and uniqueness of the solution to fSDE-Net. Our experiments demonstrate that the fSDE-Net model can replicate distributional properties well.

Improving Nonparametric Classification via Local Radial Regression with an Application to Stock Prediction

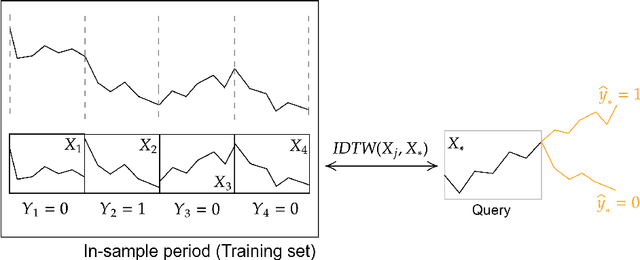
For supervised classification problems, this paper considers estimating the query's label probability through local regression using observed covariates. Well-known nonparametric kernel smoother and $k$-nearest neighbor ($k$-NN) estimator, which take label average over a ball around the query, are consistent but asymptotically biased particularly for a large radius of the ball. To eradicate such bias, local polynomial regression (LPoR) and multiscale $k$-NN (MS-$k$-NN) learn the bias term by local regression around the query and extrapolate it to the query itself. However, their theoretical optimality has been shown for the limit of the infinite number of training samples. For correcting the asymptotic bias with fewer observations, this paper proposes a local radial regression (LRR) and its logistic regression variant called local radial logistic regression (LRLR), by combining the advantages of LPoR and MS-$k$-NN. The idea is simple: we fit the local regression to observed labels by taking the radial distance as the explanatory variable and then extrapolate the estimated label probability to zero distance. Our numerical experiments, including real-world datasets of daily stock indices, demonstrate that LRLR outperforms LPoR and MS-$k$-NN.

Controlling False Discovery Rates Using Null Bootstrapping

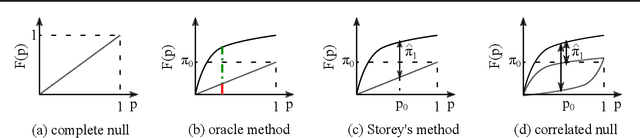
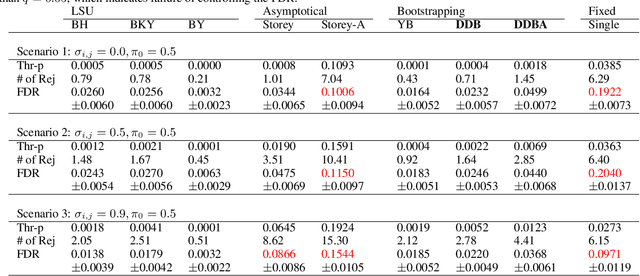
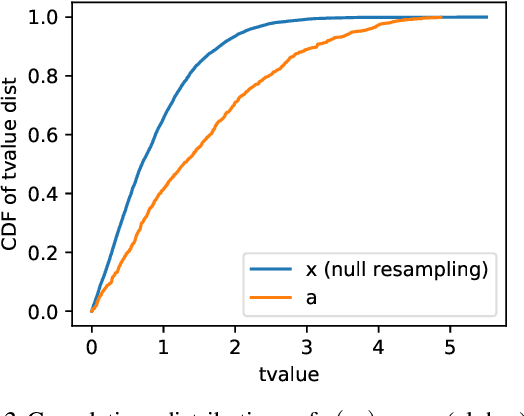
We consider controlling the false discovery rate for many tests with unknown correlation structure. Given a large number of hypotheses, false and missing discoveries can plague an analysis. While many procedures have been proposed to control false discovery, they either assume independent hypotheses or lack statistical power. We propose a novel method for false discovery control using null bootstrapping. By bootstrapping from the correlated null, we achieve superior statistical power to existing methods and prove that the false discovery rate is controlled. Simulated examples illustrate the efficacy of our method over existing methods. We apply our proposed methodology to financial asset pricing, where the goal is to determine which "factors" lead to excess returns out of a large number of potential factors.

Trader-Company Method: A Metaheuristic for Interpretable Stock Price Prediction

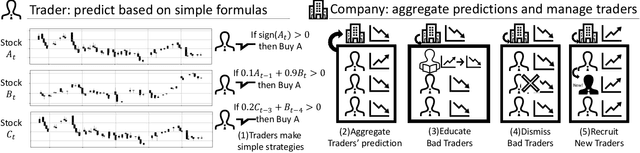
Investors try to predict returns of financial assets to make successful investment. Many quantitative analysts have used machine learning-based methods to find unknown profitable market rules from large amounts of market data. However, there are several challenges in financial markets hindering practical applications of machine learning-based models. First, in financial markets, there is no single model that can consistently make accurate prediction because traders in markets quickly adapt to newly available information. Instead, there are a number of ephemeral and partially correct models called "alpha factors". Second, since financial markets are highly uncertain, ensuring interpretability of prediction models is quite important to make reliable trading strategies. To overcome these challenges, we propose the Trader-Company method, a novel evolutionary model that mimics the roles of a financial institute and traders belonging to it. Our method predicts future stock returns by aggregating suggestions from multiple weak learners called Traders. A Trader holds a collection of simple mathematical formulae, each of which represents a candidate of an alpha factor and would be interpretable for real-world investors. The aggregation algorithm, called a Company, maintains multiple Traders. By randomly generating new Traders and retraining them, Companies can efficiently find financially meaningful formulae whilst avoiding overfitting to a transient state of the market. We show the effectiveness of our method by conducting experiments on real market data.

Deep Portfolio Optimization via Distributional Prediction of Residual Factors

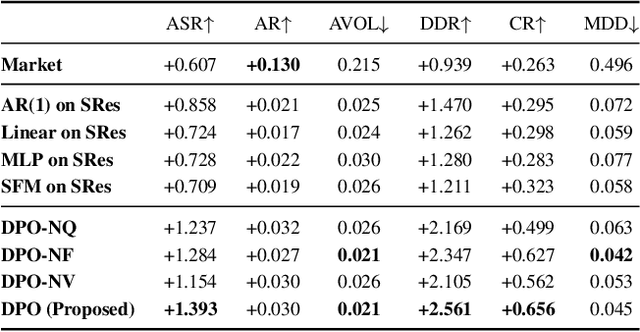
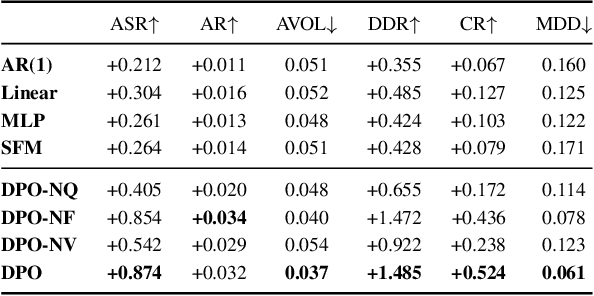
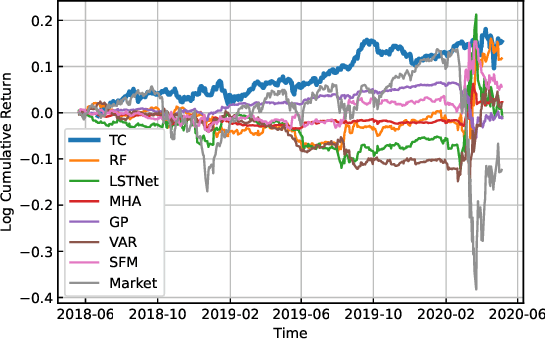
Recent developments in deep learning techniques have motivated intensive research in machine learning-aided stock trading strategies. However, since the financial market has a highly non-stationary nature hindering the application of typical data-hungry machine learning methods, leveraging financial inductive biases is important to ensure better sample efficiency and robustness. In this study, we propose a novel method of constructing a portfolio based on predicting the distribution of a financial quantity called residual factors, which is known to be generally useful for hedging the risk exposure to common market factors. The key technical ingredients are twofold. First, we introduce a computationally efficient extraction method for the residual information, which can be easily combined with various prediction algorithms. Second, we propose a novel neural network architecture that allows us to incorporate widely acknowledged financial inductive biases such as amplitude invariance and time-scale invariance. We demonstrate the efficacy of our method on U.S. and Japanese stock market data. Through ablation experiments, we also verify that each individual technique contributes to improving the performance of trading strategies. We anticipate our techniques may have wide applications in various financial problems.

Policy Gradient with Expected Quadratic Utility Maximization: A New Mean-Variance Approach in Reinforcement Learning

In real-world decision-making problems, risk management is critical. Among various risk management approaches, the mean-variance criterion is one of the most widely used in practice. In this paper, we suggest expected quadratic utility maximization (EQUM) as a new framework for policy gradient style reinforcement learning (RL) algorithms with mean-variance control. The quadratic utility function is a common objective of risk management in finance and economics. The proposed EQUM framework has several interpretations, such as reward-constrained variance minimization and regularization, as well as agent utility maximization. In addition, the computation of the EQUM framework is easier than that of existing mean-variance RL methods, which require double sampling. In experiments, we demonstrate the effectiveness of the proposed framework in the benchmarks of RL and financial data.

TPLVM: Portfolio Construction by Student's $t$-process Latent Variable Model

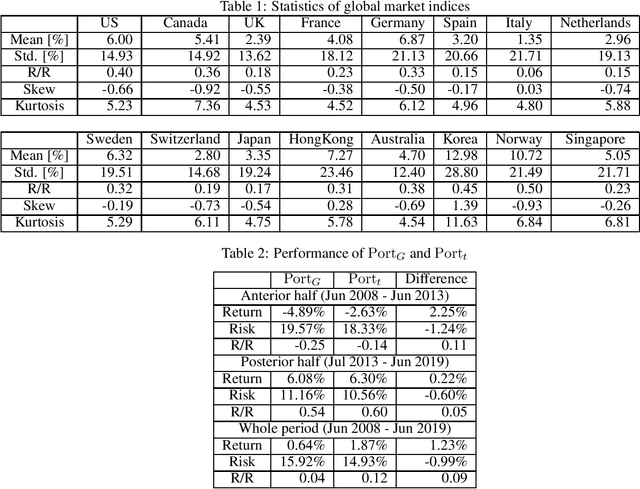
Optimal asset allocation is a key topic in modern finance theory. To realize the optimal asset allocation on investor's risk aversion, various portfolio construction methods have been proposed. Recently, the applications of machine learning are rapidly growing in the area of finance. In this article, we propose the Student's $t$-process latent variable model (TPLVM) to describe non-Gaussian fluctuations of financial timeseries by lower dimensional latent variables. Subsequently, we apply the TPLVM to minimum-variance portfolio as an alternative of existing nonlinear factor models. To test the performance of the proposed portfolio, we construct minimum-variance portfolios of global stock market indices based on the TPLVM or Gaussian process latent variable model. By comparing these portfolios, we confirm the proposed portfolio outperforms that of the existing Gaussian process latent variable model.

A Robust Transferable Deep Learning Framework for Cross-sectional Investment Strategy

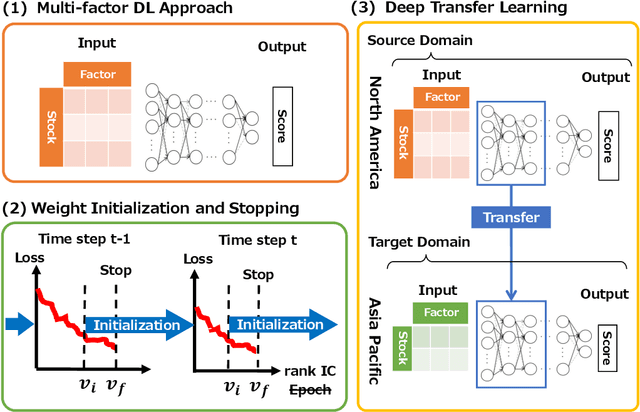
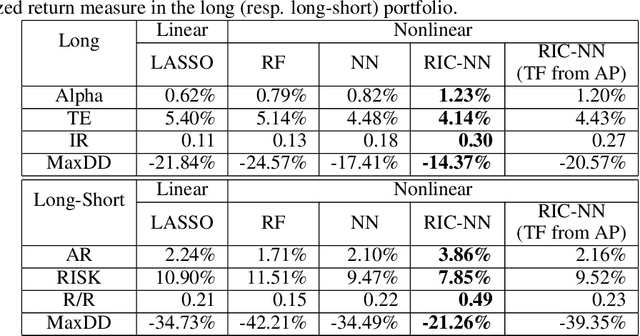
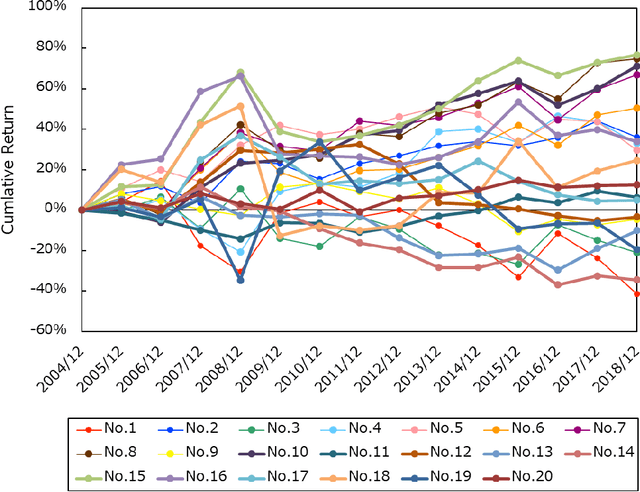
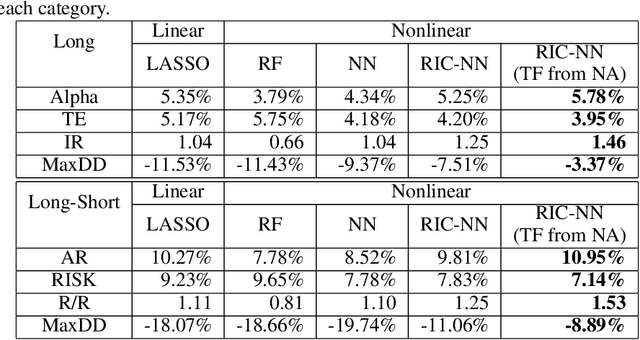
Stock return predictability is an important research theme as it reflects our economic and social organization, and significant efforts are made to explain the dynamism therein. Statistics of strong explanative power, called "factor" have been proposed to summarize the essence of predictive stock returns. Although machine learning methods are increasingly popular in stock return prediction, an inference of the stock returns is highly elusive, and still most investors, if partly, rely on their intuition to build a better decision making. The challenge here is to make an investment strategy that is consistent over a reasonably long period, with the minimum human decision on the entire process. To this end, we propose a new stock return prediction framework that we call Ranked Information Coefficient Neural Network (RIC-NN). RIC-NN is a deep learning approach and includes the following three novel ideas: (1) nonlinear multi-factor approach, (2) stopping criteria with ranked information coefficient (rank IC), and (3) deep transfer learning among multiple regions. Experimental comparison with the stocks in the Morgan Stanley Capital International (MSCI) indices shows that RIC-NN outperforms not only off-the-shelf machine learning methods but also the average return of major equity investment funds in the last fourteen years.