Synthetic Control Methods by Density Matching under Implicit Endogeneity

Synthetic control methods (SCMs) have become a crucial tool for causal inference in comparative case studies. The fundamental idea of SCMs is to estimate counterfactual outcomes for a treated unit by using a weighted sum of observed outcomes from untreated units. The accuracy of the synthetic control (SC) is critical for estimating the causal effect, and hence, the estimation of SC weights has been the focus of much research. In this paper, we first point out that existing SCMs suffer from an implicit endogeneity problem, which is the correlation between the outcomes of untreated units and the error term in the model of a counterfactual outcome. We show that this problem yields a bias in the causal effect estimator. We then propose a novel SCM based on density matching, assuming that the density of outcomes of the treated unit can be approximated by a weighted average of the densities of untreated units (i.e., a mixture model). Based on this assumption, we estimate SC weights by matching moments of treated outcomes and the weighted sum of moments of untreated outcomes. Our proposed method has three advantages over existing methods. First, our estimator is asymptotically unbiased under the assumption of the mixture model. Second, due to the asymptotic unbiasedness, we can reduce the mean squared error for counterfactual prediction. Third, our method generates full densities of the treatment effect, not only expected values, which broadens the applicability of SCMs. We provide experimental results to demonstrate the effectiveness of our proposed method.

Spatially-Varying Bayesian Predictive Synthesis for Flexible and Interpretable Spatial Prediction

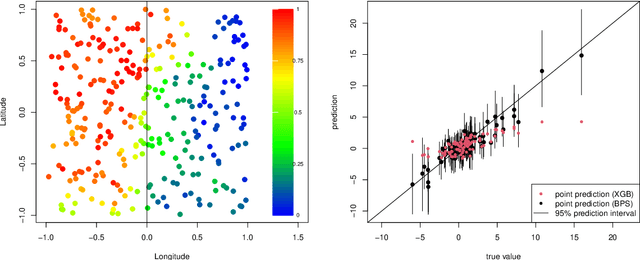
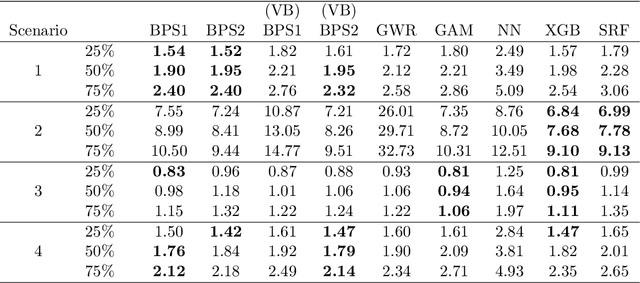
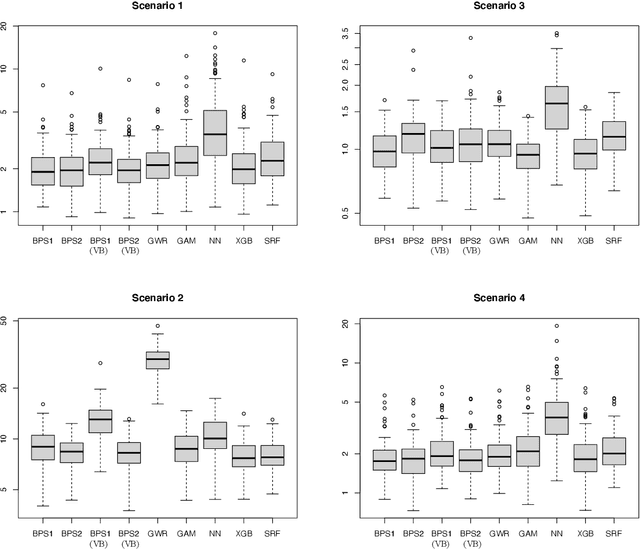
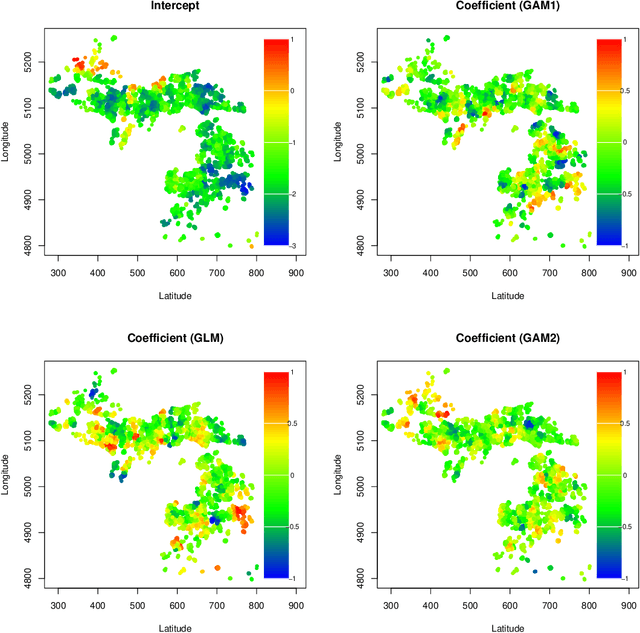
Spatial data are characterized by their spatial dependence, which is often complex, non-linear, and difficult to capture with a single model. Significant levels of model uncertainty -- arising from these characteristics -- cannot be resolved by model selection or simple ensemble methods, as performances are not homogeneous. We address this issue by proposing a novel methodology that captures spatially-varying model uncertainty, which we call spatial Bayesian predictive synthesis. Our proposal is defined by specifying a latent factor spatially-varying coefficient model as the synthesis function, which enables model coefficients to vary over the region to achieve flexible spatial model ensembling. Two MCMC strategies are implemented for full uncertainty quantification, as well as a variational inference strategy for fast point inference. We also extend the estimations strategy for general responses. A finite sample theoretical guarantee is given for the predictive performance of our methodology, showing that the predictions are exact minimax. Through simulation examples and two real data applications, we demonstrate that our proposed spatial Bayesian predictive synthesis outperforms standard spatial models and advanced machine learning methods, in terms of predictive accuracy, while maintaining interpretability of the prediction mechanism.

Policy Choice and Best Arm Identification: Comments on "Adaptive Treatment Assignment in Experiments for Policy Choice"

Adaptive experimental design for efficient decision-making is an important problem in economics. The purpose of this paper is to connect the "policy choice" problem, proposed in Kasy and Sautmann (2021) as an instance of adaptive experimental design, to the frontiers of the bandit literature in machine learning. We discuss how the policy choice problem can be framed in a way such that it is identical to what is called the "best arm identification" (BAI) problem. By connecting the literature, we identify that the asymptotic optimality of policy choice algorithms tackled in Kasy and Sautmann (2021) is a long-standing open question in the literature. While Kasy and Sautmann (2021) presents an interesting and important empirical study, unfortunately, this connection highlights several major issues with the theoretical results. In particular, we show that Theorem 1 in Kasy and Sautmann (2021) is false. We find that the proofs of statements (1) and (2) of Theorem 1 are incorrect. Although the statements themselves may be true, they are non-trivial to fix. Statement (3), and its proof, on the other hand, is false, which we show by utilizing existing theoretical results in the bandit literature. As this question is critically important, garnering much interest in the last decade within the bandit community, we provide a review of recent developments in the BAI literature. We hope this serves to highlight the relevance to economic problems and stimulate methodological and theoretical developments in the econometric community.

Learning Causal Relationships from Conditional Moment Conditions by Importance Weighting

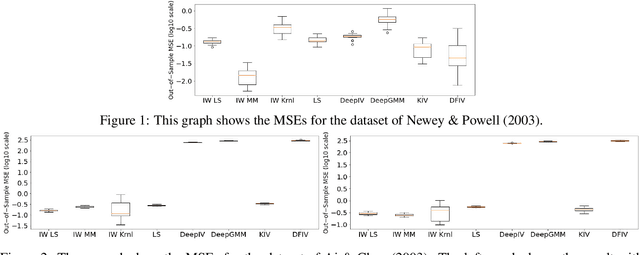
We consider learning causal relationships under conditional moment conditions. Unlike causal inference under unconditional moment conditions, conditional moment conditions pose serious challenges for causal inference, especially in complex, high-dimensional settings. To address this issue, we propose a method that transforms conditional moment conditions to unconditional moment conditions through importance weighting using the conditional density ratio. Then, using this transformation, we propose a method that successfully approximates conditional moment conditions. Our proposed approach allows us to employ methods for estimating causal parameters from unconditional moment conditions, such as generalized method of moments, adequately in a straightforward manner. In experiments, we confirm that our proposed method performs well compared to existing methods.

Controlling False Discovery Rates Using Null Bootstrapping

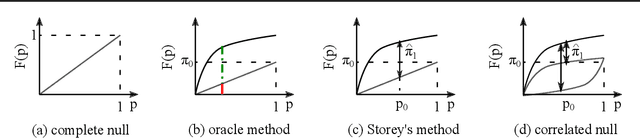
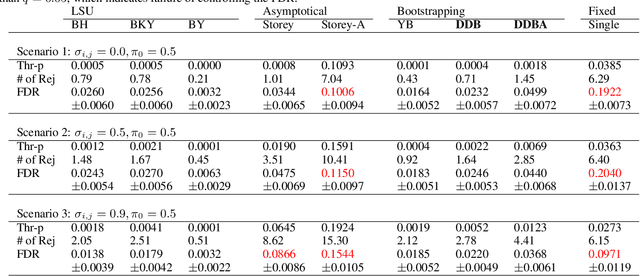
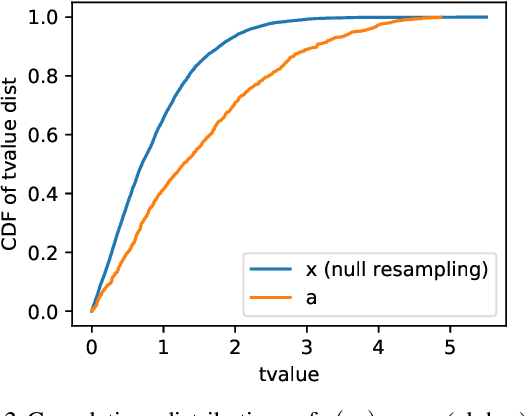
We consider controlling the false discovery rate for many tests with unknown correlation structure. Given a large number of hypotheses, false and missing discoveries can plague an analysis. While many procedures have been proposed to control false discovery, they either assume independent hypotheses or lack statistical power. We propose a novel method for false discovery control using null bootstrapping. By bootstrapping from the correlated null, we achieve superior statistical power to existing methods and prove that the false discovery rate is controlled. Simulated examples illustrate the efficacy of our method over existing methods. We apply our proposed methodology to financial asset pricing, where the goal is to determine which "factors" lead to excess returns out of a large number of potential factors.

Predictive properties of forecast combination, ensemble methods, and Bayesian predictive synthesis

This paper studies the theoretical predictive properties of classes of forecast combination methods. A novel strategy based on continuous time stochastic processes is proposed and developed, where the combined predictive error processes are expressed as stochastic differential equations, evaluated using Ito's lemma. We identify a class of forecast combination methods, which we categorize as non-linear synthesis, and find that it entails an extra term in the predictive error process that "corrects" the bias from misspecification and dependence amongst forecasts, effectively improving forecasts. We show that a subclass of the recently developed framework of Bayesian predictive synthesis fits within this class. Theoretical properties are examined and we show that non-linear synthesis improves the expected squared forecast error over any and all linear combination, averaging, and ensemble of forecasts, under mild conditions that are met in most real applications. We discuss the conditions for which non-linear synthesis outperforms linear combinations, and its implications for developing further strategies. A finite sample simulation study is presented to illustrate our results.