Controlling False Discovery Rates Using Null Bootstrapping
Paper and Code
Feb 15, 2021
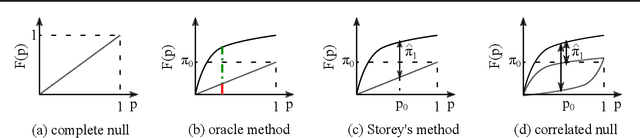
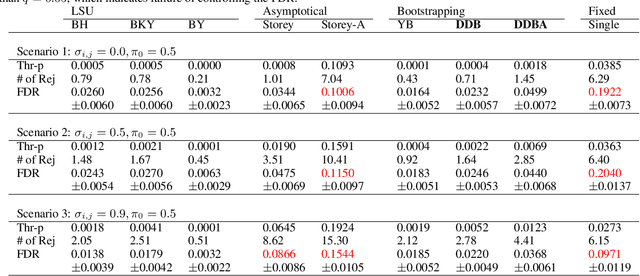
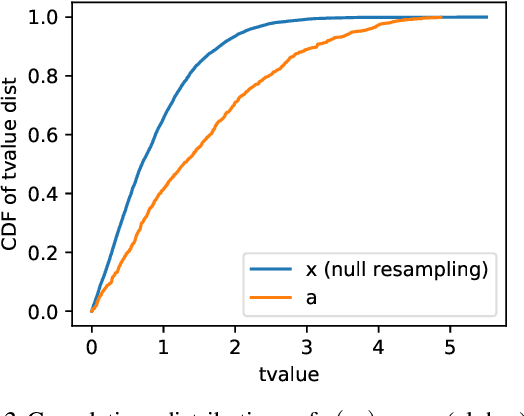
We consider controlling the false discovery rate for many tests with unknown correlation structure. Given a large number of hypotheses, false and missing discoveries can plague an analysis. While many procedures have been proposed to control false discovery, they either assume independent hypotheses or lack statistical power. We propose a novel method for false discovery control using null bootstrapping. By bootstrapping from the correlated null, we achieve superior statistical power to existing methods and prove that the false discovery rate is controlled. Simulated examples illustrate the efficacy of our method over existing methods. We apply our proposed methodology to financial asset pricing, where the goal is to determine which "factors" lead to excess returns out of a large number of potential factors.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge