Statistical mechanical analysis of sparse linear regression as a variable selection problem

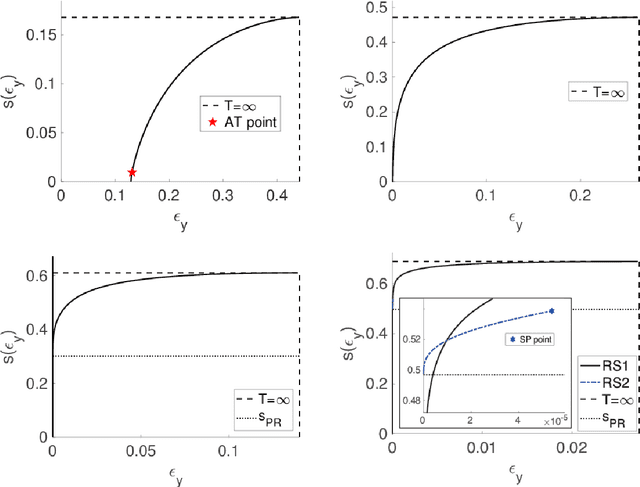
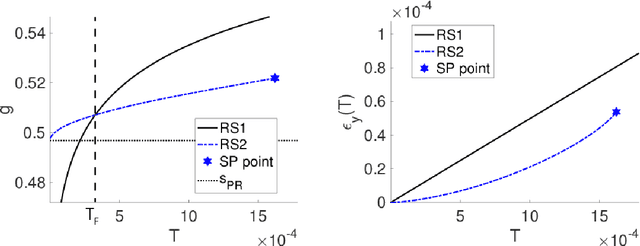
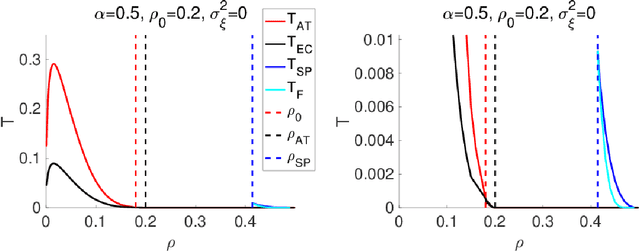
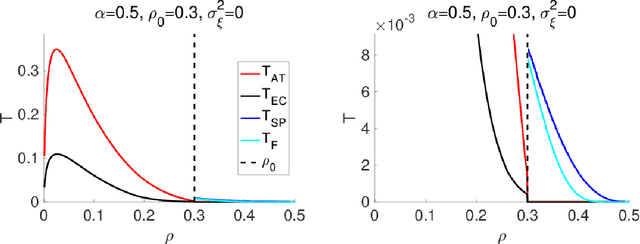
An algorithmic limit of compressed sensing or related variable-selection problems is analytically evaluated when a design matrix is given by an overcomplete random matrix. The replica method from statistical mechanics is employed to derive the result. The analysis is conducted through evaluation of the entropy, an exponential rate of the number of combinations of variables giving a specific value of fit error to given data which is assumed to be generated from a linear process using the design matrix. This yields the typical achievable limit of the fit error when solving a representative $\ell_0$ problem and includes the presence of unfavourable phase transitions preventing local search algorithms from reaching the minimum-error configuration. The associated phase diagrams are presented. A noteworthy outcome of the phase diagrams is that there exists a wide parameter region where any phase transition is absent from the high temperature to the lowest temperature at which the minimum-error configuration or the ground state is reached. This implies that certain local search algorithms can find the ground state with moderate computational costs in that region. Another noteworthy result is the presence of the random first-order transition in the strong noise case. The theoretical evaluation of the entropy is confirmed by extensive numerical methods using the exchange Monte Carlo and the multi-histogram methods. Another numerical test based on a metaheuristic optimisation algorithm called simulated annealing is conducted, which well supports the theoretical predictions on the local search algorithms. In the successful region with no phase transition, the computational cost of the simulated annealing to reach the ground state is estimated as the third order polynomial of the model dimensionality.

Exhaustive search for sparse variable selection in linear regression

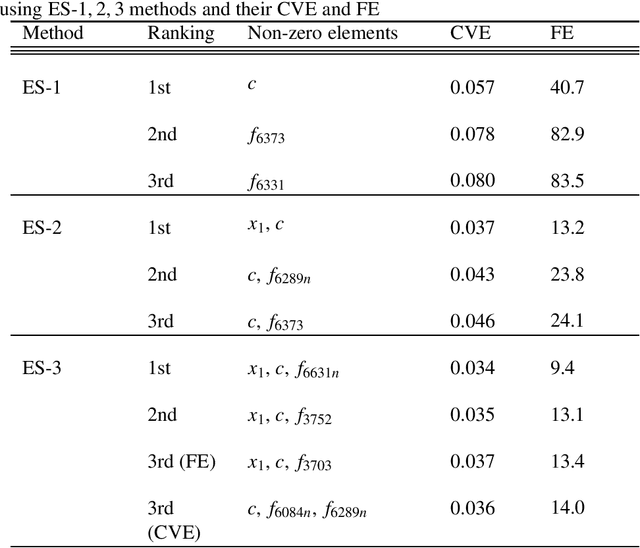
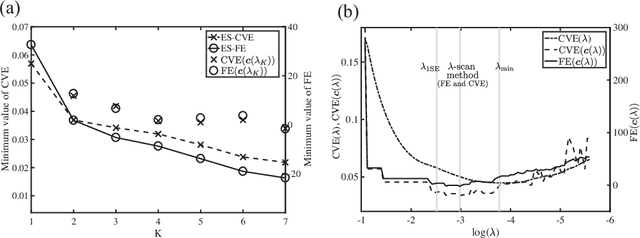
We propose a K-sparse exhaustive search (ES-K) method and a K-sparse approximate exhaustive search method (AES-K) for selecting variables in linear regression. With these methods, K-sparse combinations of variables are tested exhaustively assuming that the optimal combination of explanatory variables is K-sparse. By collecting the results of exhaustively computing ES-K, various approximate methods for selecting sparse variables can be summarized as density of states. With this density of states, we can compare different methods for selecting sparse variables such as relaxation and sampling. For large problems where the combinatorial explosion of explanatory variables is crucial, the AES-K method enables density of states to be effectively reconstructed by using the replica-exchange Monte Carlo method and the multiple histogram method. Applying the ES-K and AES-K methods to type Ia supernova data, we confirmed the conventional understanding in astronomy when an appropriate K is given beforehand. However, we found the difficulty to determine K from the data. Using virtual measurement and analysis, we argue that this is caused by data shortage.