Algebraic Geometrical Analysis of Metropolis Algorithm When Parameters Are Non-identifiable

The Metropolis algorithm is one of the Markov chain Monte Carlo (MCMC) methods that realize sampling from the target probability distribution. In this paper, we are concerned with the sampling from the distribution in non-identifiable cases that involve models with Fisher information matrices that may fail to be invertible. The theoretical adjustment of the step size, which is the variance of the candidate distribution, is difficult for non-identifiable cases. In this study, to establish such a principle, the average acceptance rate, which is used as a guideline to optimize the step size in the MCMC method, was analytically derived in non-identifiable cases. The optimization principle for the step size was developed from the viewpoint of the average acceptance rate. In addition, we performed numerical experiments on some specific target distributions to verify the effectiveness of our theoretical results.

Sequential Experimental Design for Spectral Measurement: Active Learning Using a Parametric Model

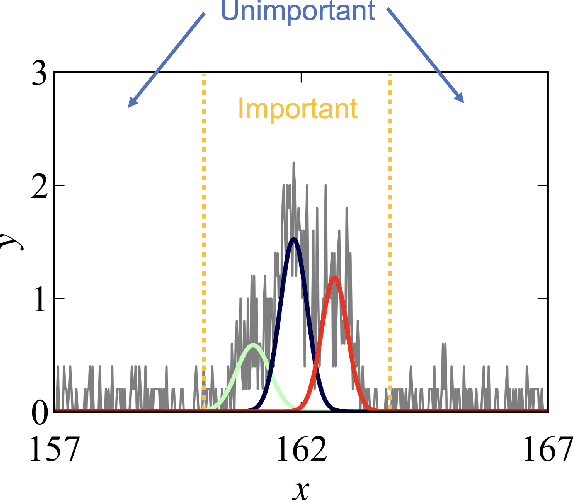
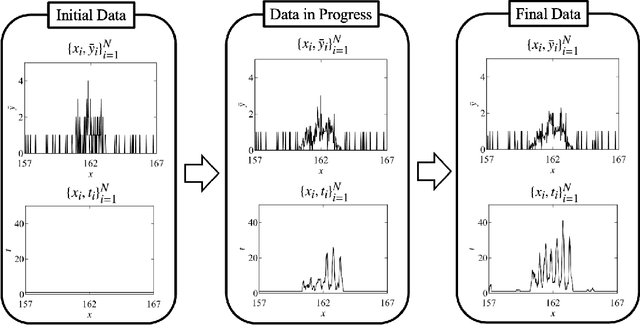
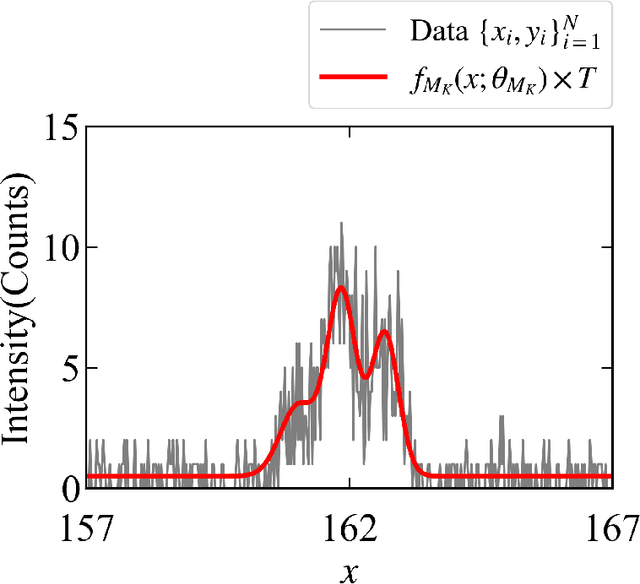
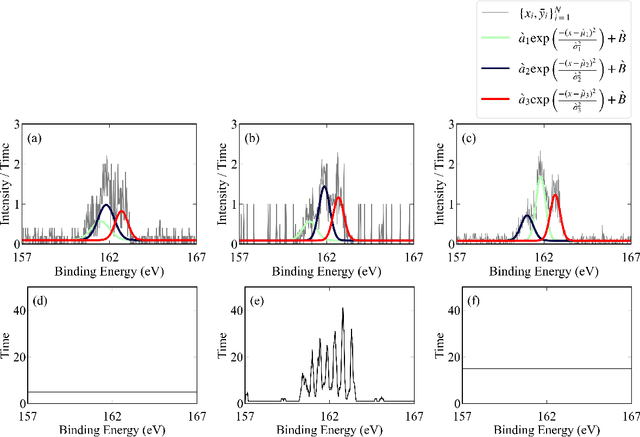
In this study, we demonstrate a sequential experimental design for spectral measurements by active learning using parametric models as predictors. In spectral measurements, it is necessary to reduce the measurement time because of sample fragility and high energy costs. To improve the efficiency of experiments, sequential experimental designs are proposed, in which the subsequent measurement is designed by active learning using the data obtained before the measurement. Conventionally, parametric models are employed in data analysis; when employed for active learning, they are expected to afford a sequential experimental design that improves the accuracy of data analysis. However, due to the complexity of the formulas, a sequential experimental design using general parametric models has not been realized. Therefore, we applied Bayesian inference-based data analysis using the exchange Monte Carlo method to realize a sequential experimental design with general parametric models. In this study, we evaluated the effectiveness of the proposed method by applying it to Bayesian spectral deconvolution and Bayesian Hamiltonian selection in X-ray photoelectron spectroscopy. Using numerical experiments with artificial data, we demonstrated that the proposed method improves the accuracy of model selection and parameter estimation while reducing the measurement time compared with the results achieved without active learning or with active learning using the Gaussian process regression.

Bayesian Spectral Deconvolution Based on Poisson Distribution: Bayesian Measurement and Virtual Measurement Analytics (VMA)

In this paper, we propose a new method of Bayesian measurement for spectral deconvolution, which regresses spectral data into the sum of unimodal basis function such as Gaussian or Lorentzian functions. Bayesian measurement is a framework for considering not only the target physical model but also the measurement model as a probabilistic model, and enables us to estimate the parameter of a physical model with its confidence interval through a Bayesian posterior distribution given a measurement data set. The measurement with Poisson noise is one of the most effective system to apply our proposed method. Since the measurement time is strongly related to the signal-to-noise ratio for the Poisson noise model, Bayesian measurement with Poisson noise model enables us to clarify the relationship between the measurement time and the limit of estimation. In this study, we establish the probabilistic model with Poisson noise for spectral deconvolution. Bayesian measurement enables us to perform virtual and computer simulation for a certain measurement through the established probabilistic model. This property is called "Virtual Measurement Analytics(VMA)" in this paper. We also show that the relationship between the measurement time and the limit of estimation can be extracted by using the proposed method in a simulation of synthetic data and real data for XPS measurement of MoS$_2$.

Simultaneous Estimation of Noise Variance and Number of Peaks in Bayesian Spectral Deconvolution

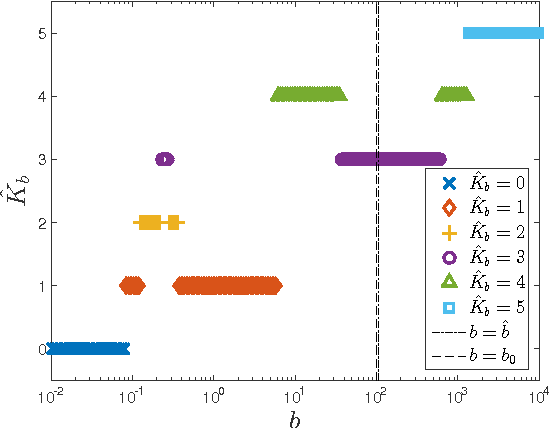
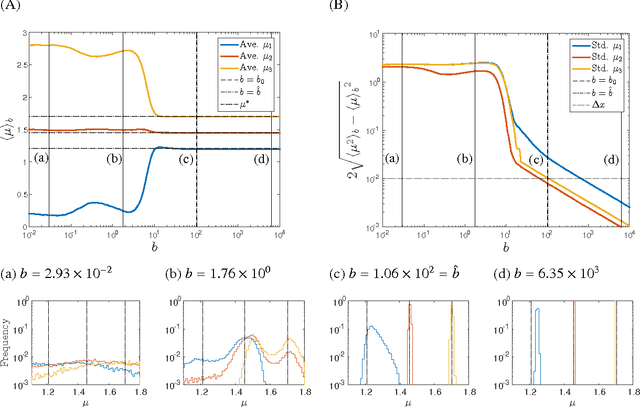
The heuristic identification of peaks from noisy complex spectra often leads to misunderstanding of the physical and chemical properties of matter. In this paper, we propose a framework based on Bayesian inference, which enables us to separate multipeak spectra into single peaks statistically and consists of two steps. The first step is estimating both the noise variance and the number of peaks as hyperparameters based on Bayes free energy, which generally is not analytically tractable. The second step is fitting the parameters of each peak function to the given spectrum by calculating the posterior density, which has a problem of local minima and saddles since multipeak models are nonlinear and hierarchical. Our framework enables the escape from local minima or saddles by using the exchange Monte Carlo method and calculates Bayes free energy via the multiple histogram method. We discuss a simulation demonstrating how efficient our framework is and show that estimating both the noise variance and the number of peaks prevents overfitting, overpenalizing, and misunderstanding the precision of parameter estimation.