Recursive Construction of Stable Assemblies of Recurrent Neural Networks

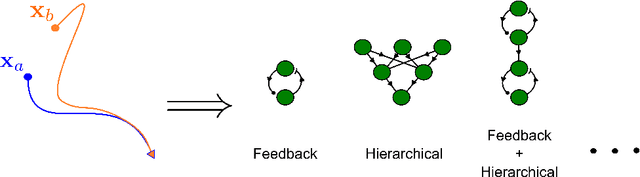
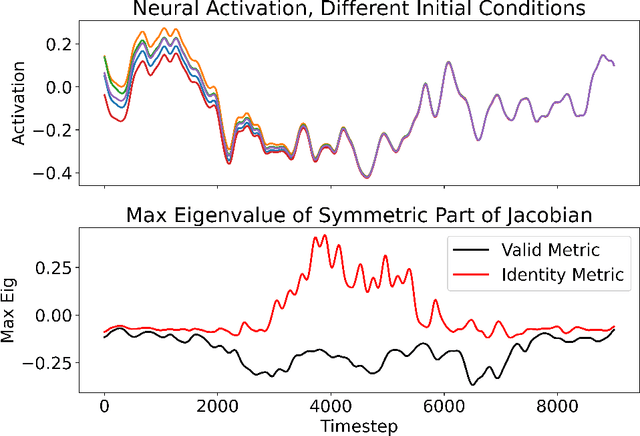
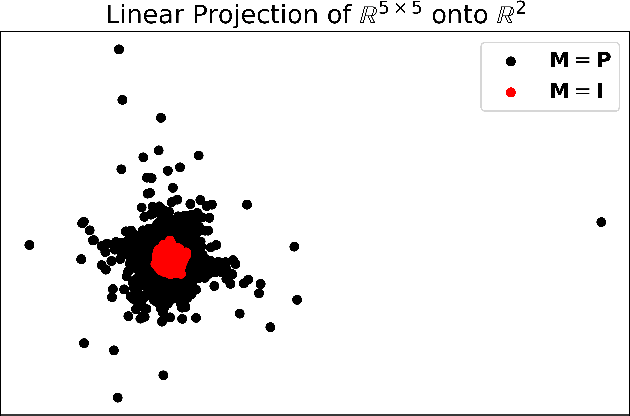
Advanced applications of modern machine learning will likely involve combinations of trained networks, as are already used in spectacular systems such as DeepMind's AlphaGo. Recursively building such combinations in an effective and stable fashion while also allowing for continual refinement of the individual networks - as nature does for biological networks - will require new analysis tools. This paper takes a step in this direction by establishing contraction properties of broad classes of nonlinear recurrent networks and neural ODEs, and showing how these quantified properties allow in turn to recursively construct stable networks of networks in a systematic fashion. The results can also be used to stably combine recurrent networks and physical systems with quantified contraction properties. Similarly, they may be applied to modular computational models of cognition.