Moses C. Nah
Modular Robot Control with Motor Primitives
May 15, 2025Abstract:Despite a slow neuromuscular system, humans easily outperform modern robot technology, especially in physical contact tasks. How is this possible? Biological evidence indicates that motor control of biological systems is achieved by a modular organization of motor primitives, which are fundamental building blocks of motor behavior. Inspired by neuro-motor control research, the idea of using simpler building blocks has been successfully used in robotics. Nevertheless, a comprehensive formulation of modularity for robot control remains to be established. In this paper, we introduce a modular framework for robot control using motor primitives. We present two essential requirements to achieve modular robot control: independence of modules and closure of stability. We describe key control modules and demonstrate that a wide range of complex robotic behaviors can be generated from this small set of modules and their combinations. The presented modular control framework demonstrates several beneficial properties for robot control, including task-space control without solving Inverse Kinematics, addressing the problems of kinematic singularity and kinematic redundancy, and preserving passivity for contact and physical interactions. Further advantages include exploiting kinematic singularity to maintain high external load with low torque compensation, as well as controlling the robot beyond its end-effector, extending even to external objects. Both simulation and actual robot experiments are presented to validate the effectiveness of our modular framework. We conclude that modularity may be an effective constructive framework for achieving robotic behaviors comparable to human-level performance.
A Physically Consistent Stiffness Formulation for Contact-Rich Manipulation
Mar 09, 2025Abstract:Ensuring symmetric stiffness in impedance-controlled robots is crucial for physically meaningful and stable interaction in contact-rich manipulation. Conventional approaches neglect the change of basis vectors in curved spaces, leading to an asymmetric joint-space stiffness matrix that violates passivity and conservation principles. In this work, we derive a physically consistent, symmetric joint-space stiffness formulation directly from the task-space stiffness matrix by explicitly incorporating Christoffel symbols. This correction resolves long-standing inconsistencies in stiffness modeling, ensuring energy conservation and stability. We validate our approach experimentally on a robotic system, demonstrating that omitting these correction terms results in significant asymmetric stiffness errors. Our findings bridge theoretical insights with practical control applications, offering a robust framework for stable and interpretable robotic interactions.
Combining Movement Primitives with Contraction Theory
Jan 15, 2025Abstract:This paper presents a modular framework for motion planning using movement primitives. Central to the approach is Contraction Theory, a modular stability tool for nonlinear dynamical systems. The approach extends prior methods by achieving parallel and sequential combinations of both discrete and rhythmic movements, while enabling independent modulation of each movement. This modular framework enables a divide-and-conquer strategy to simplify the programming of complex robot motion planning. Simulation examples illustrate the flexibility and versatility of the framework, highlighting its potential to address diverse challenges in robot motion planning.
Divide et Impera: Learning impedance families for peg-in-hole assembly
Oct 01, 2024


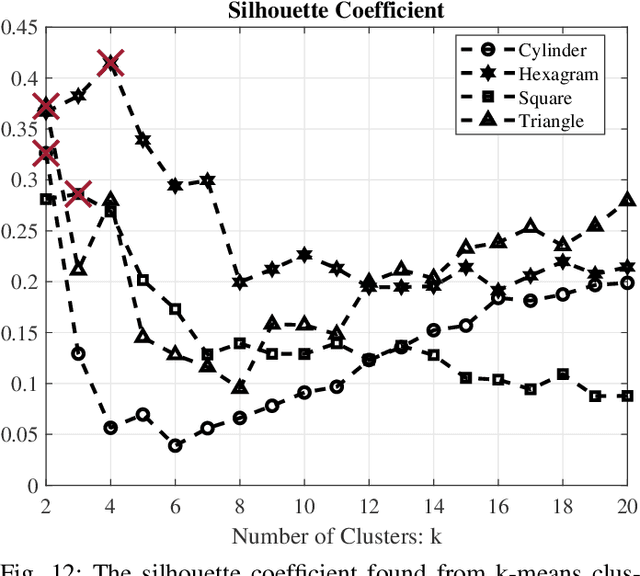
Abstract:This paper addresses robotic peg-in-hole assembly using the framework of Elementary Dynamic Actions (EDA). Inspired by motor primitives in neuromotor control research, the method leverages three primitives: submovements, oscillations, and mechanical impedances (e.g., stiffness and damping), combined via a Norton equivalent network model. By focusing on impedance parameterization, we explore the adaptability of EDA in contact-rich tasks. Experimental results, conducted on a real robot setup with four different peg types, demonstrated a range of successful impedance parameters, challenging conventional methods that seek optimal parameters. We analyze our data in a lower-dimensional solution space. Clustering analysis shows the possibility to identify different individual strategies for each single peg, as well as common strategies across all pegs. A neural network model, trained on the experimental data, accurately predicted successful impedance parameters across all pegs. The practical utility of this work is enhanced by a success-predictor model and the public availability of all code and CAD files. These findings highlight the flexibility and robustness of EDA; show multiple equally-successful strategies for contact-rich manipulation; and offer valuable insights and tools for robotic assembly programming.
Robot Control based on Motor Primitives -- A Comparison of Two Approaches
Oct 28, 2023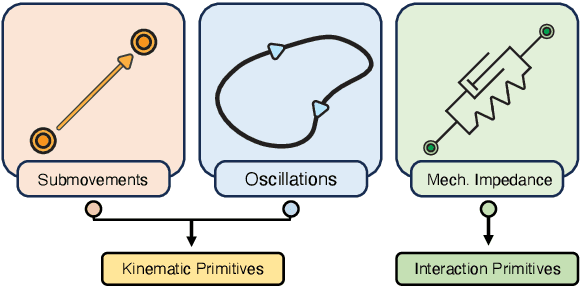
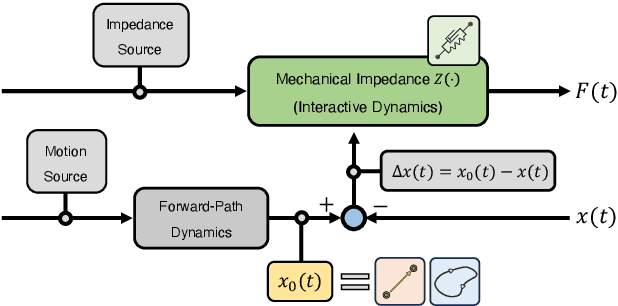
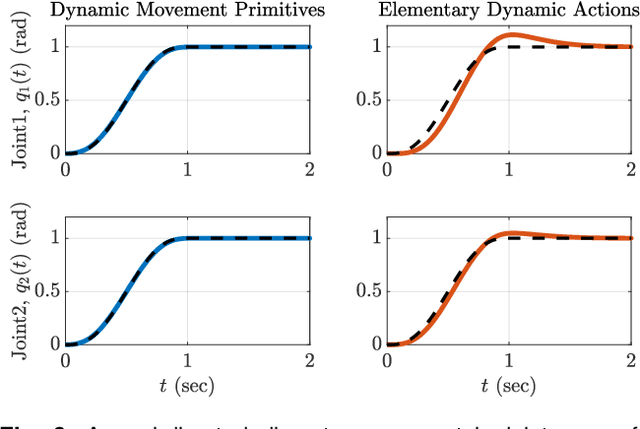
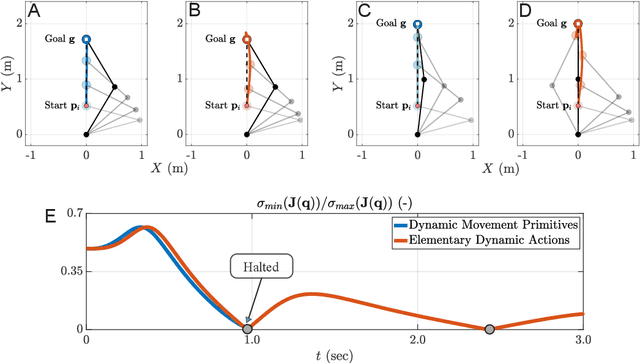
Abstract:Motor primitives are fundamental building blocks of a controller which enable dynamic robot behavior with minimal high-level intervention. By treating motor primitives as basic "modules," different modules can be sequenced or superimposed to generate a rich repertoire of motor behavior. In robotics, two distinct approaches have been proposed: Dynamic Movement Primitives (DMPs) and Elementary Dynamic Actions (EDAs). While both approaches instantiate similar ideas, significant differences also exist. This paper attempts to clarify the distinction and provide a unifying view by delineating the similarities and differences between DMPs and EDAs. We provide eight robot control examples, including sequencing or superimposing movements, managing kinematic redundancy and singularity, obstacle avoidance, and managing physical interaction. We show that the two approaches clearly diverge in their implementation. We also discuss how DMPs and EDAs might be combined to get the best of both approaches. With this detailed comparison, we enable researchers to make informed decisions to select the most suitable approach for specific robot tasks and applications.
Kinematic Modularity of Elementary Dynamic Actions
Sep 26, 2023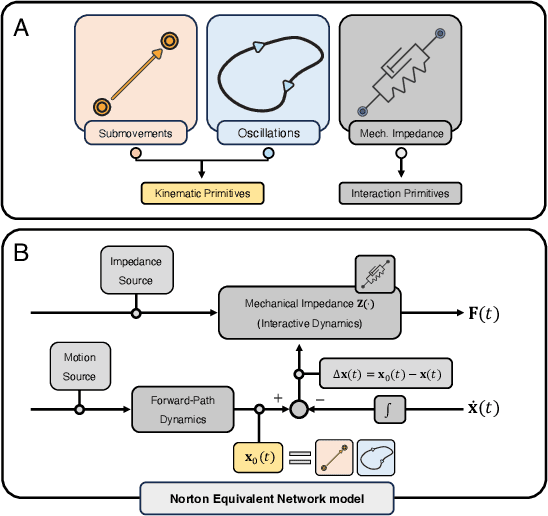
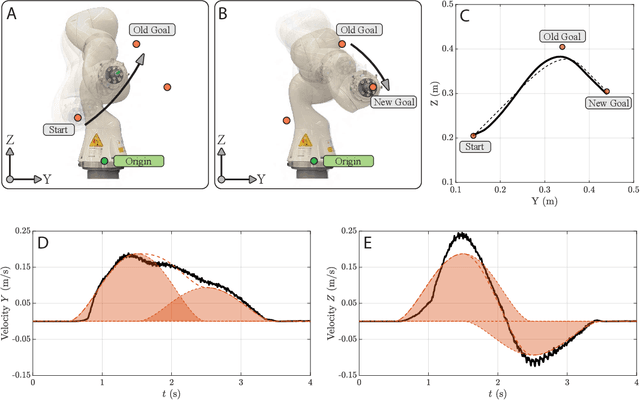
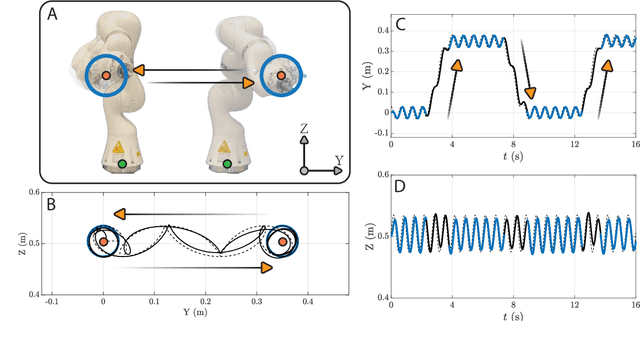
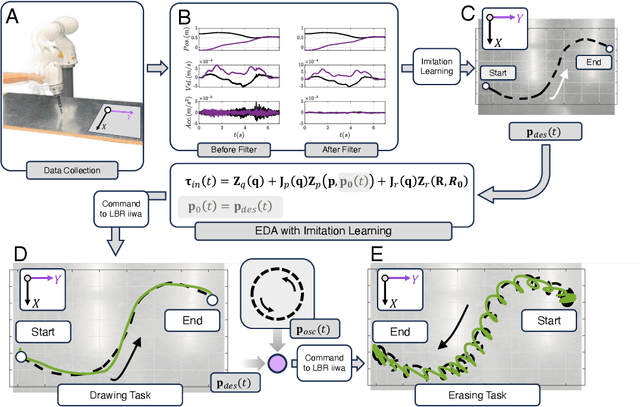
Abstract:In this paper, a kinematically modular approach to robot control is presented. The method involves structures called Elementary Dynamic Actions and a network model combining these elements. With this control framework, a rich repertoire of movements can be generated by combination of basic kinematic modules. Each module can be learned by Imitation Learning, thereby resulting in a modular learning strategy for robot control. The theoretical foundations and their real robot implementation are presented. Using a KUKA LBR iiwa14 robot, three tasks were considered: (1) generating a sequence of discrete movements, (2) generating a combination of discrete and rhythmic movements, and (3) a drawing and erasing task. The obtained results indicate that this modular approach has the potential to simplify the generation of a diverse range of robot actions.
Exp-A Robot modeling Software based on Exponential Maps
Sep 13, 2023Abstract:$ $Deriving a robot's equation of motion typically requires placing multiple coordinate frames, commonly using the Denavit-Hartenberg convention to express the kinematic and dynamic relationships between segments. This paper presents an alternative using the differential geometric method of Exponential Maps, which reduces the number of coordinate frame choices to two. The traditional and differential geometric methods are compared, and the conceptual and practical differences are detailed. The open-source software, Exp[licit], based on the differential geometric method, is introduced. It is intended for use by researchers and engineers with basic knowledge of geometry and robotics. Code snippets and an example application are provided to demonstrate the benefits of the differential geometric method and assist users to get started with the software.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge