Divide et Impera: Learning impedance families for peg-in-hole assembly

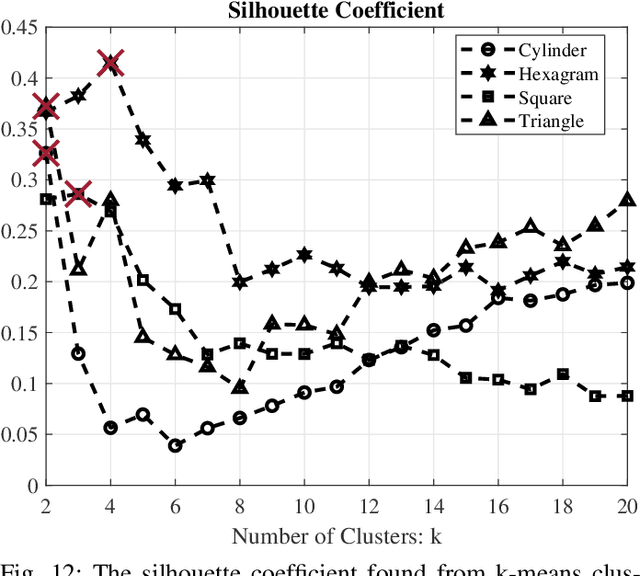
This paper addresses robotic peg-in-hole assembly using the framework of Elementary Dynamic Actions (EDA). Inspired by motor primitives in neuromotor control research, the method leverages three primitives: submovements, oscillations, and mechanical impedances (e.g., stiffness and damping), combined via a Norton equivalent network model. By focusing on impedance parameterization, we explore the adaptability of EDA in contact-rich tasks. Experimental results, conducted on a real robot setup with four different peg types, demonstrated a range of successful impedance parameters, challenging conventional methods that seek optimal parameters. We analyze our data in a lower-dimensional solution space. Clustering analysis shows the possibility to identify different individual strategies for each single peg, as well as common strategies across all pegs. A neural network model, trained on the experimental data, accurately predicted successful impedance parameters across all pegs. The practical utility of this work is enhanced by a success-predictor model and the public availability of all code and CAD files. These findings highlight the flexibility and robustness of EDA; show multiple equally-successful strategies for contact-rich manipulation; and offer valuable insights and tools for robotic assembly programming.

Surpassing Cosine Similarity for Multidimensional Comparisons: Dimension Insensitive Euclidean Metric (DIEM)

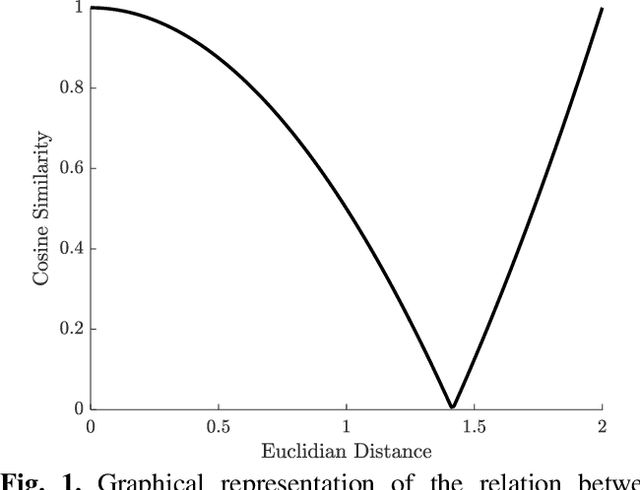
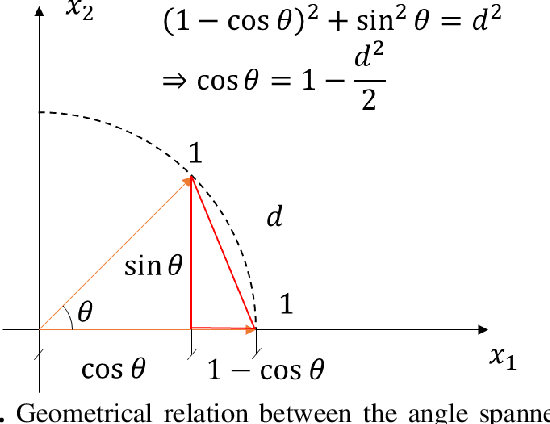
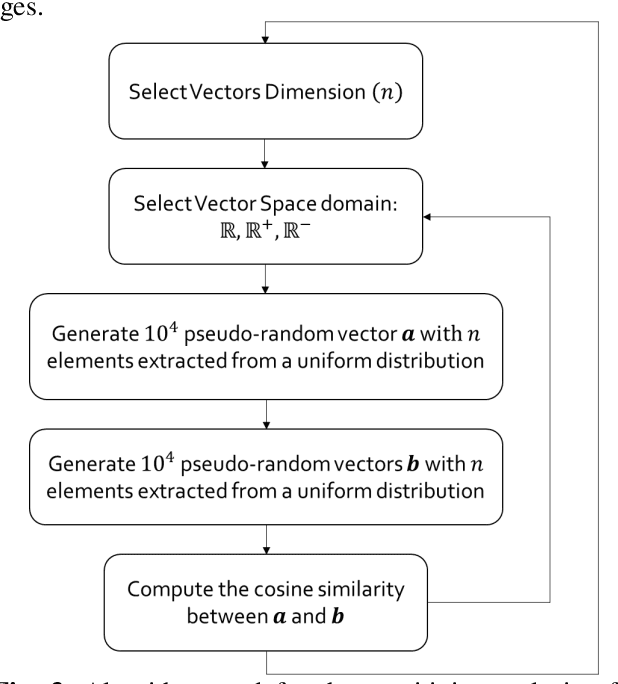
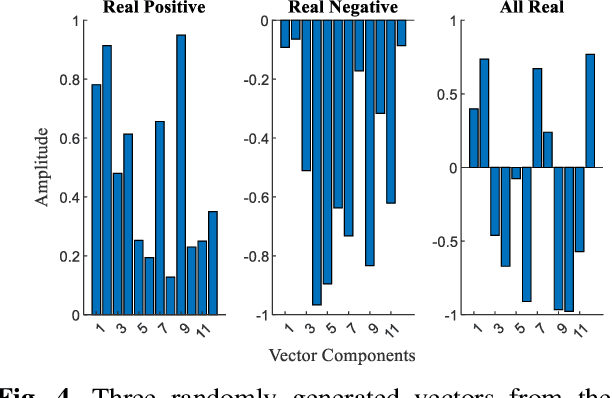
The advancement in computational power and hardware efficiency has enabled the tackling of increasingly complex and high-dimensional problems. While artificial intelligence (AI) has achieved remarkable results in various scientific and technological fields, the interpretability of these high-dimensional solutions remains challenging. A critical issue in this context is the comparison of multidimensional quantities, which is essential in techniques like Principal Component Analysis (PCA), Singular Value Decomposition (SVD), and k-means clustering. Common metrics such as cosine similarity, Euclidean distance, and Manhattan distance are often used for such comparisons - for example in muscular synergies of the human motor control system. However, their applicability and interpretability diminish as dimensionality increases. This paper provides a comprehensive analysis of the effects of dimensionality on these three widely used metrics. Our results reveal significant limitations of cosine similarity, particularly its dependency on the dimensionality of the vectors, leading to biased and less interpretable outcomes. To address this, we introduce the Dimension Insensitive Euclidean Metric (DIEM), derived from the Euclidean distance, which demonstrates superior robustness and generalizability across varying dimensions. DIEM maintains consistent variability and eliminates the biases observed in traditional metrics, making it a more reliable tool for high-dimensional comparisons. This novel metric has the potential to replace cosine similarity, providing a more accurate and insightful method to analyze multidimensional data in fields ranging from neuromotor control to machine learning and deep learning.

Kinematic Modularity of Elementary Dynamic Actions

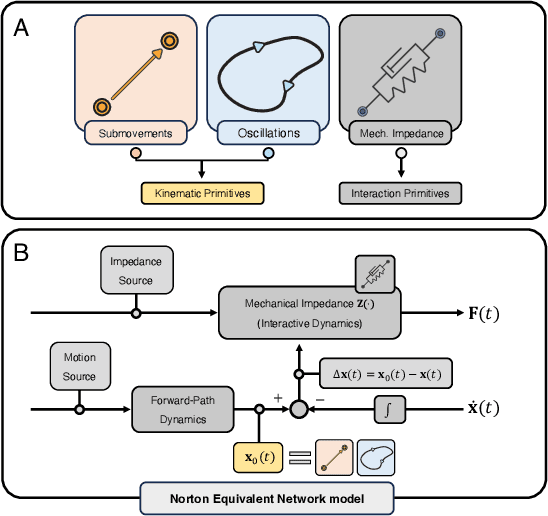
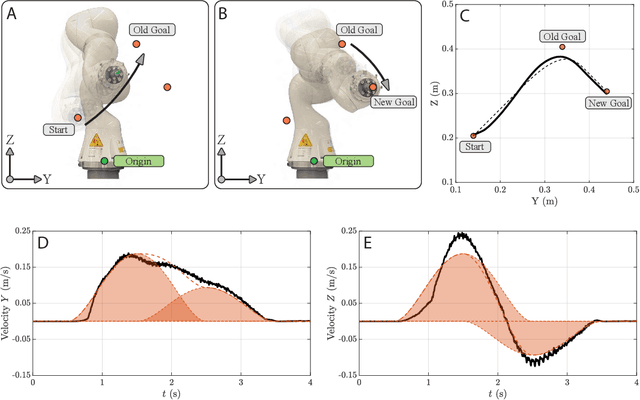
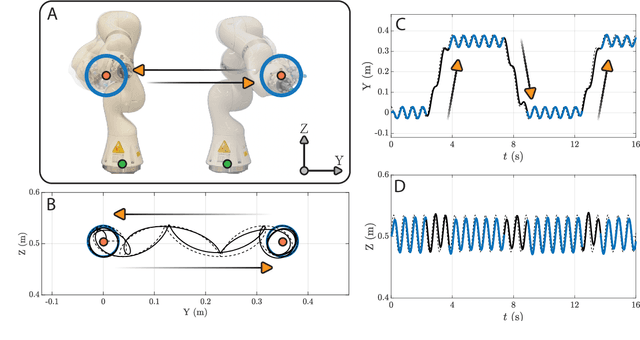
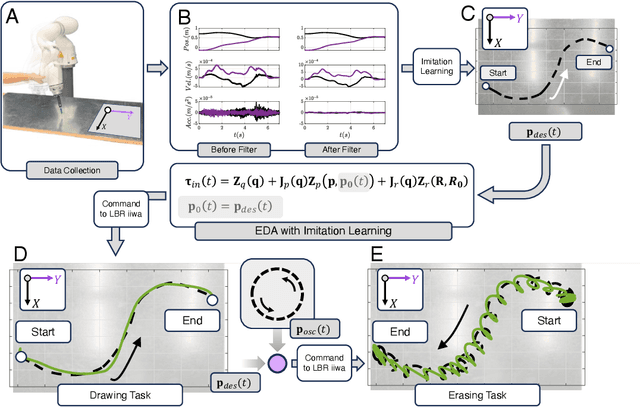
In this paper, a kinematically modular approach to robot control is presented. The method involves structures called Elementary Dynamic Actions and a network model combining these elements. With this control framework, a rich repertoire of movements can be generated by combination of basic kinematic modules. Each module can be learned by Imitation Learning, thereby resulting in a modular learning strategy for robot control. The theoretical foundations and their real robot implementation are presented. Using a KUKA LBR iiwa14 robot, three tasks were considered: (1) generating a sequence of discrete movements, (2) generating a combination of discrete and rhythmic movements, and (3) a drawing and erasing task. The obtained results indicate that this modular approach has the potential to simplify the generation of a diverse range of robot actions.