Divide et Impera: Learning impedance families for peg-in-hole assembly

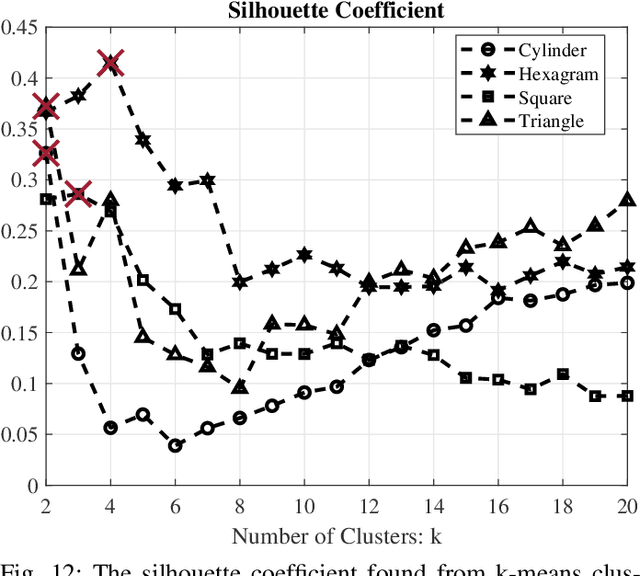
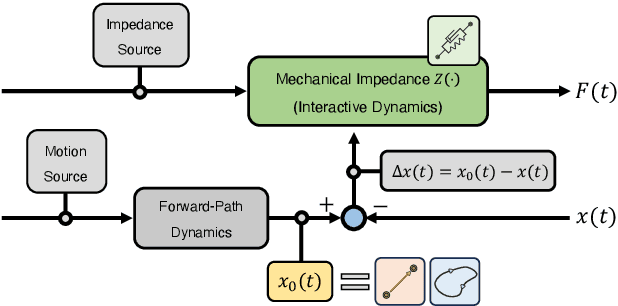
This paper addresses robotic peg-in-hole assembly using the framework of Elementary Dynamic Actions (EDA). Inspired by motor primitives in neuromotor control research, the method leverages three primitives: submovements, oscillations, and mechanical impedances (e.g., stiffness and damping), combined via a Norton equivalent network model. By focusing on impedance parameterization, we explore the adaptability of EDA in contact-rich tasks. Experimental results, conducted on a real robot setup with four different peg types, demonstrated a range of successful impedance parameters, challenging conventional methods that seek optimal parameters. We analyze our data in a lower-dimensional solution space. Clustering analysis shows the possibility to identify different individual strategies for each single peg, as well as common strategies across all pegs. A neural network model, trained on the experimental data, accurately predicted successful impedance parameters across all pegs. The practical utility of this work is enhanced by a success-predictor model and the public availability of all code and CAD files. These findings highlight the flexibility and robustness of EDA; show multiple equally-successful strategies for contact-rich manipulation; and offer valuable insights and tools for robotic assembly programming.

Surpassing Cosine Similarity for Multidimensional Comparisons: Dimension Insensitive Euclidean Metric (DIEM)

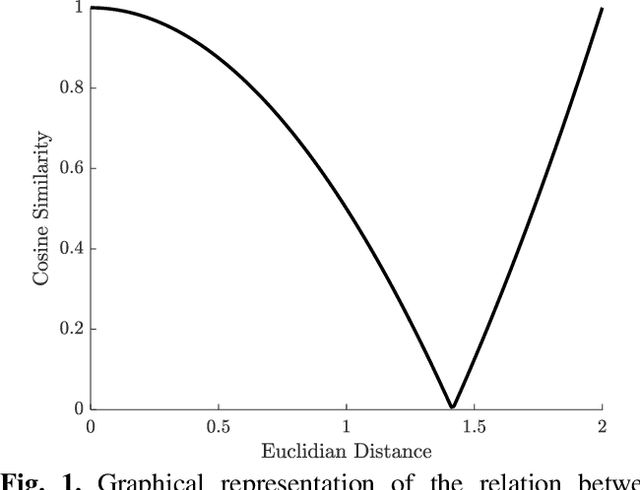
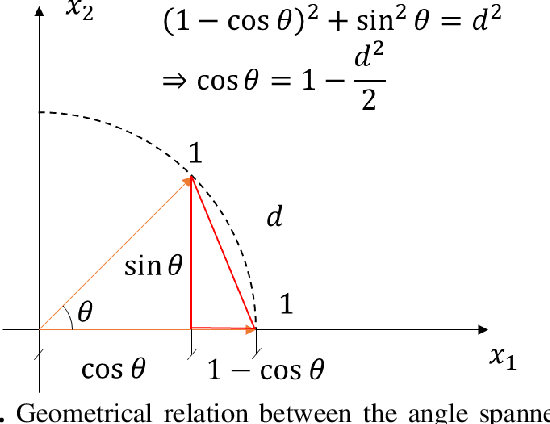
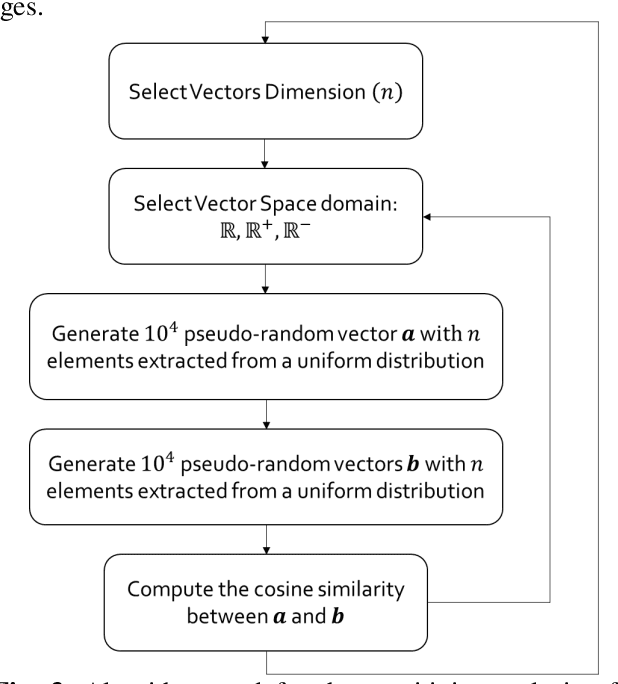
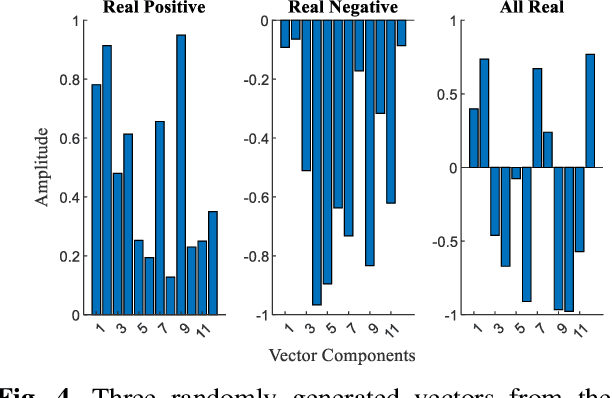
The advancement in computational power and hardware efficiency has enabled the tackling of increasingly complex and high-dimensional problems. While artificial intelligence (AI) has achieved remarkable results in various scientific and technological fields, the interpretability of these high-dimensional solutions remains challenging. A critical issue in this context is the comparison of multidimensional quantities, which is essential in techniques like Principal Component Analysis (PCA), Singular Value Decomposition (SVD), and k-means clustering. Common metrics such as cosine similarity, Euclidean distance, and Manhattan distance are often used for such comparisons - for example in muscular synergies of the human motor control system. However, their applicability and interpretability diminish as dimensionality increases. This paper provides a comprehensive analysis of the effects of dimensionality on these three widely used metrics. Our results reveal significant limitations of cosine similarity, particularly its dependency on the dimensionality of the vectors, leading to biased and less interpretable outcomes. To address this, we introduce the Dimension Insensitive Euclidean Metric (DIEM), derived from the Euclidean distance, which demonstrates superior robustness and generalizability across varying dimensions. DIEM maintains consistent variability and eliminates the biases observed in traditional metrics, making it a more reliable tool for high-dimensional comparisons. This novel metric has the potential to replace cosine similarity, providing a more accurate and insightful method to analyze multidimensional data in fields ranging from neuromotor control to machine learning and deep learning.

Robot Control based on Motor Primitives -- A Comparison of Two Approaches

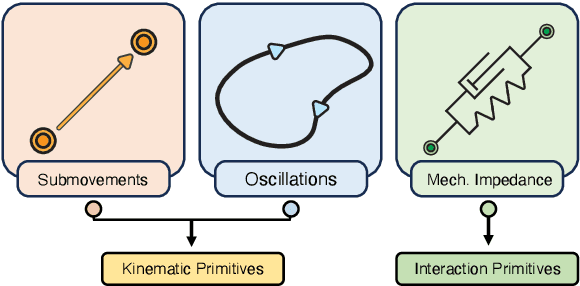
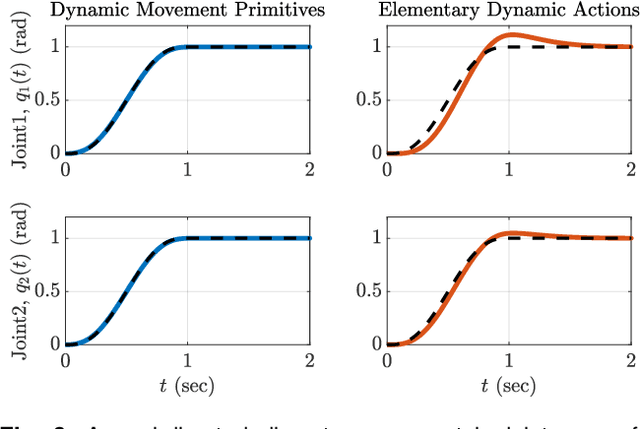
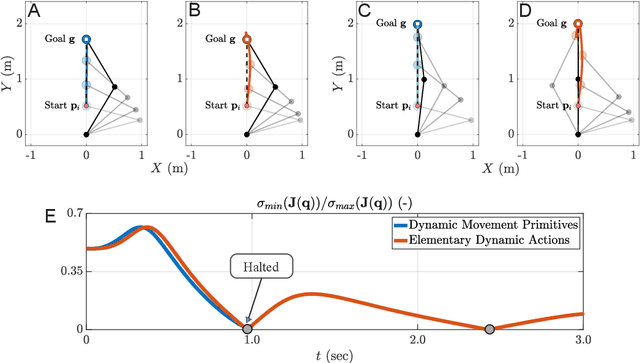
Motor primitives are fundamental building blocks of a controller which enable dynamic robot behavior with minimal high-level intervention. By treating motor primitives as basic "modules," different modules can be sequenced or superimposed to generate a rich repertoire of motor behavior. In robotics, two distinct approaches have been proposed: Dynamic Movement Primitives (DMPs) and Elementary Dynamic Actions (EDAs). While both approaches instantiate similar ideas, significant differences also exist. This paper attempts to clarify the distinction and provide a unifying view by delineating the similarities and differences between DMPs and EDAs. We provide eight robot control examples, including sequencing or superimposing movements, managing kinematic redundancy and singularity, obstacle avoidance, and managing physical interaction. We show that the two approaches clearly diverge in their implementation. We also discuss how DMPs and EDAs might be combined to get the best of both approaches. With this detailed comparison, we enable researchers to make informed decisions to select the most suitable approach for specific robot tasks and applications.

Kinematic Modularity of Elementary Dynamic Actions

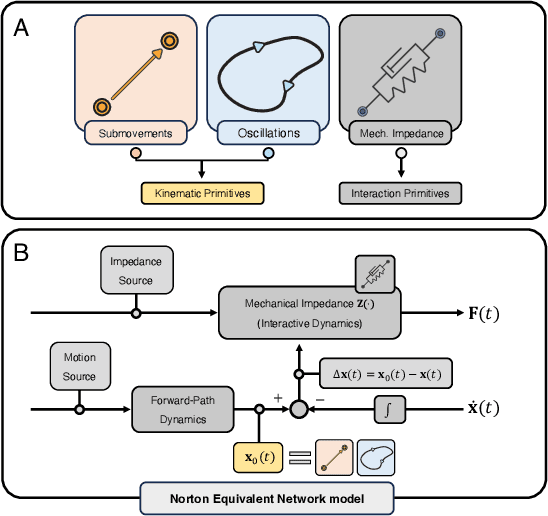
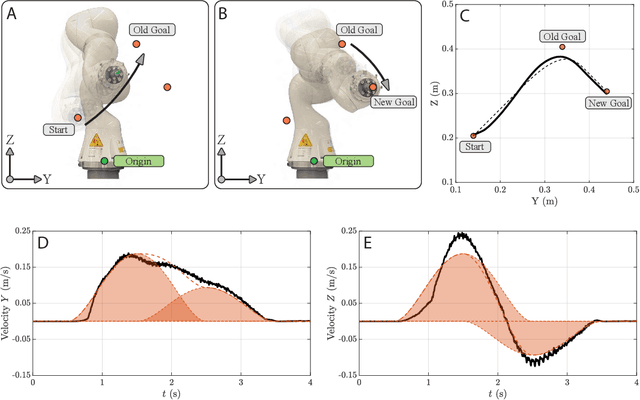
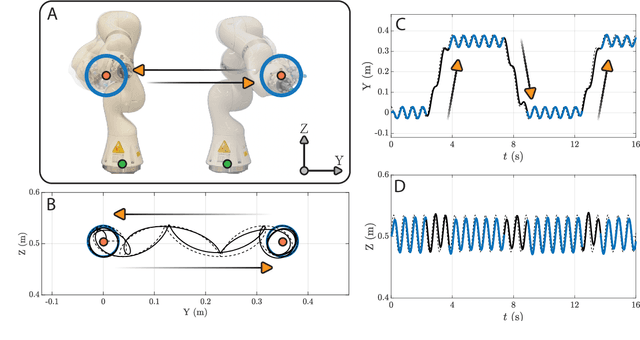
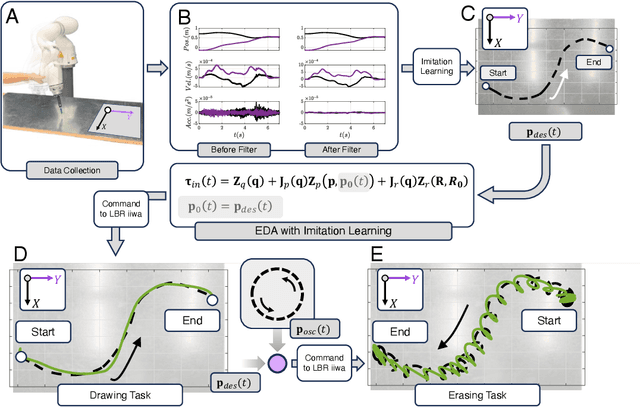
In this paper, a kinematically modular approach to robot control is presented. The method involves structures called Elementary Dynamic Actions and a network model combining these elements. With this control framework, a rich repertoire of movements can be generated by combination of basic kinematic modules. Each module can be learned by Imitation Learning, thereby resulting in a modular learning strategy for robot control. The theoretical foundations and their real robot implementation are presented. Using a KUKA LBR iiwa14 robot, three tasks were considered: (1) generating a sequence of discrete movements, (2) generating a combination of discrete and rhythmic movements, and (3) a drawing and erasing task. The obtained results indicate that this modular approach has the potential to simplify the generation of a diverse range of robot actions.

Exp-A Robot modeling Software based on Exponential Maps

$ $Deriving a robot's equation of motion typically requires placing multiple coordinate frames, commonly using the Denavit-Hartenberg convention to express the kinematic and dynamic relationships between segments. This paper presents an alternative using the differential geometric method of Exponential Maps, which reduces the number of coordinate frame choices to two. The traditional and differential geometric methods are compared, and the conceptual and practical differences are detailed. The open-source software, Exp[licit], based on the differential geometric method, is introduced. It is intended for use by researchers and engineers with basic knowledge of geometry and robotics. Code snippets and an example application are provided to demonstrate the benefits of the differential geometric method and assist users to get started with the software.

How does the structure embedded in learning policy affect learning quadruped locomotion?

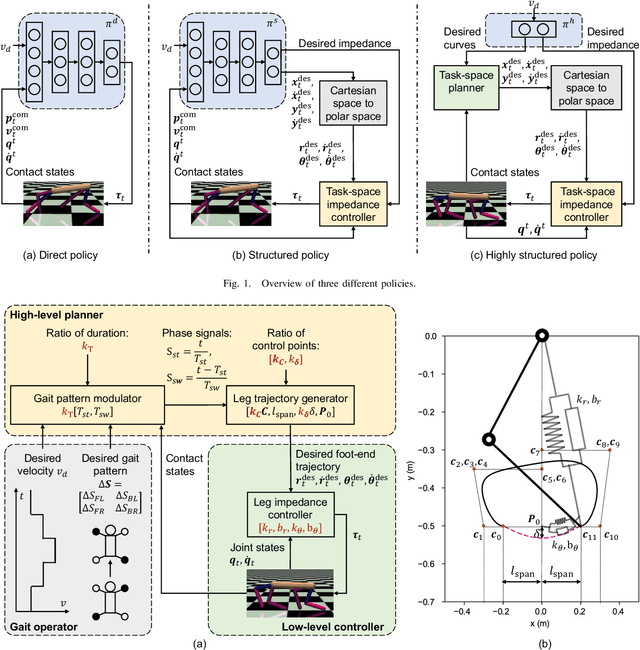
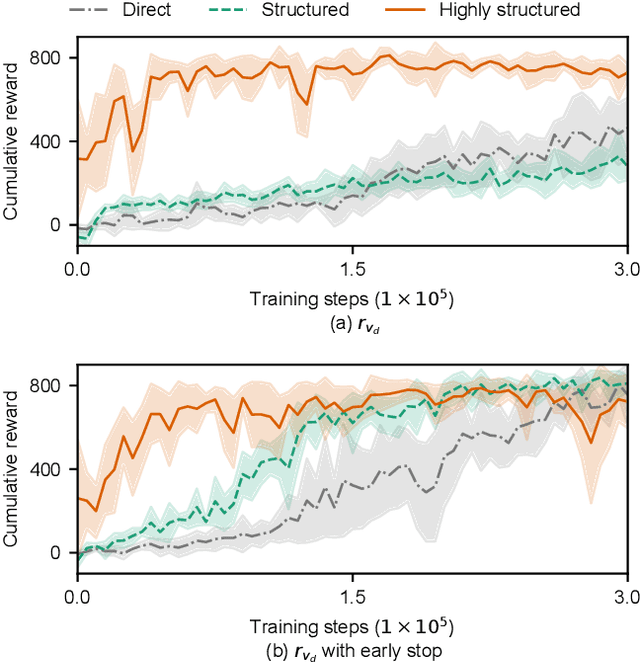
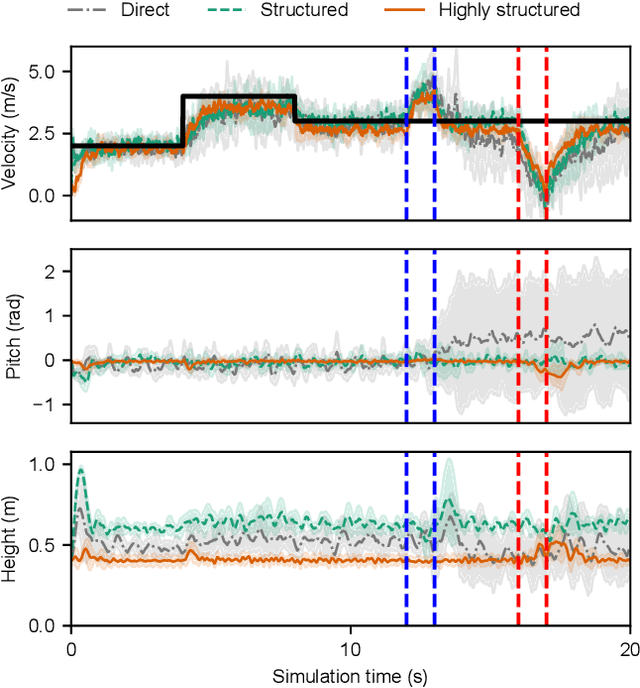
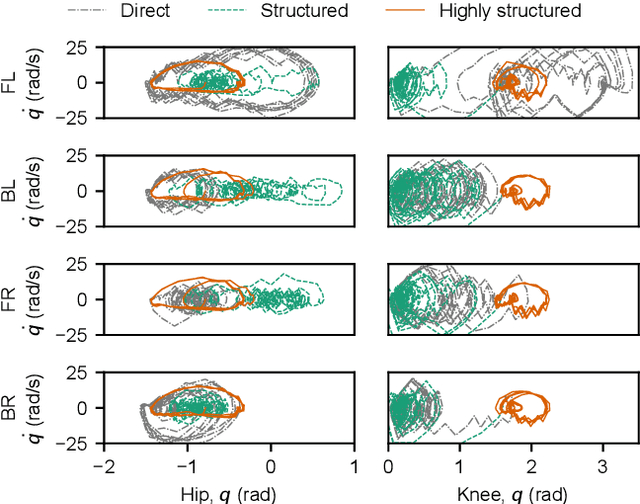
Reinforcement learning (RL) is a popular data-driven method that has demonstrated great success in robotics. Previous works usually focus on learning an end-to-end (direct) policy to directly output joint torques. While the direct policy seems convenient, the resultant performance may not meet our expectations. To improve its performance, more sophisticated reward functions or more structured policies can be utilized. This paper focuses on the latter because the structured policy is more intuitive and can inherit insights from previous model-based controllers. It is unsurprising that the structure, such as a better choice of the action space and constraints of motion trajectory, may benefit the training process and the final performance of the policy at the cost of generality, but the quantitative effect is still unclear. To analyze the effect of the structure quantitatively, this paper investigates three policies with different levels of structure in learning quadruped locomotion: a direct policy, a structured policy, and a highly structured policy. The structured policy is trained to learn a task-space impedance controller and the highly structured policy learns a controller tailored for trot running, which we adopt from previous work. To evaluate trained policies, we design a simulation experiment to track different desired velocities under force disturbances. Simulation results show that structured policy and highly structured policy require 1/3 and 3/4 fewer training steps than the direct policy to achieve a similar level of cumulative reward, and seem more robust and efficient than the direct policy. We highlight that the structure embedded in the policies significantly affects the overall performance of learning a complicated task when complex dynamics are involved, such as legged locomotion.