Stepping Out of the Shadows: Reinforcement Learning in Shadow Mode

Reinforcement learning (RL) is not yet competitive for many cyber-physical systems, such as robotics, process automation, and power systems, as training on a system with physical components cannot be accelerated, and simulation models do not exist or suffer from a large simulation-to-reality gap. During the long training time, expensive equipment cannot be used and might even be damaged due to inappropriate actions of the reinforcement learning agent. Our novel approach addresses exactly this problem: We train the reinforcement agent in a so-called shadow mode with the assistance of an existing conventional controller, which does not have to be trained and instantaneously performs reasonably well. In shadow mode, the agent relies on the controller to provide action samples and guidance towards favourable states to learn the task, while simultaneously estimating for which states the learned agent will receive a higher reward than the conventional controller. The RL agent will then control the system for these states and all other regions remain under the control of the existing controller. Over time, the RL agent will take over for an increasing amount of states, while leaving control to the baseline, where it cannot surpass its performance. Thus, we keep regret during training low and improve the performance compared to only using conventional controllers or reinforcement learning. We present and evaluate two mechanisms for deciding whether to use the RL agent or the conventional controller. The usefulness of our approach is demonstrated for a reach-avoid task, for which we are able to effectively train an agent, where standard approaches fail.

Excluding the Irrelevant: Focusing Reinforcement Learning through Continuous Action Masking

Continuous action spaces in reinforcement learning (RL) are commonly defined as interval sets. While intervals usually reflect the action boundaries for tasks well, they can be challenging for learning because the typically large global action space leads to frequent exploration of irrelevant actions. Yet, little task knowledge can be sufficient to identify significantly smaller state-specific sets of relevant actions. Focusing learning on these relevant actions can significantly improve training efficiency and effectiveness. In this paper, we propose to focus learning on the set of relevant actions and introduce three continuous action masking methods for exactly mapping the action space to the state-dependent set of relevant actions. Thus, our methods ensure that only relevant actions are executed, enhancing the predictability of the RL agent and enabling its use in safety-critical applications. We further derive the implications of the proposed methods on the policy gradient. Using Proximal Policy Optimization (PPO), we evaluate our methods on three control tasks, where the relevant action set is computed based on the system dynamics and a relevant state set. Our experiments show that the three action masking methods achieve higher final rewards and converge faster than the baseline without action masking.

MinMax Networks

While much progress has been achieved over the last decades in neuro-inspired machine learning, there are still fundamental theoretical problems in gradient-based learning using combinations of neurons. These problems, such as saddle points and suboptimal plateaus of the cost function, can lead in theory and practice to failures of learning. In addition, the discrete step size selection of the gradient is problematic since too large steps can lead to instability and too small steps slow down the learning. This paper describes an alternative discrete MinMax learning approach for continuous piece-wise linear functions. Global exponential convergence of the algorithm is established using Contraction Theory with Inequality Constraints, which is extended from the continuous to the discrete case in this paper: The parametrization of each linear function piece is, in contrast to deep learning, linear in the proposed MinMax network. This allows a linear regression stability proof as long as measurements do not transit from one linear region to its neighbouring linear region. The step size of the discrete gradient descent is Lagrangian limited orthogonal to the edge of two neighbouring linear functions. It will be shown that this Lagrangian step limitation does not decrease the convergence of the unconstrained system dynamics in contrast to a step size limitation in the direction of the gradient. We show that the convergence rate of a constrained piece-wise linear function learning is equivalent to the exponential convergence rates of the individual local linear regions.

Notes on stable learning with piecewise-linear basis functions

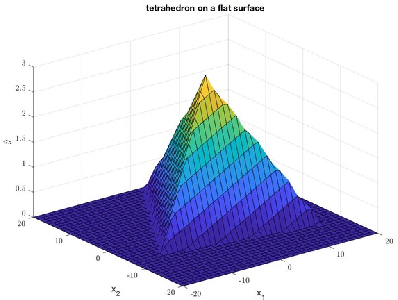
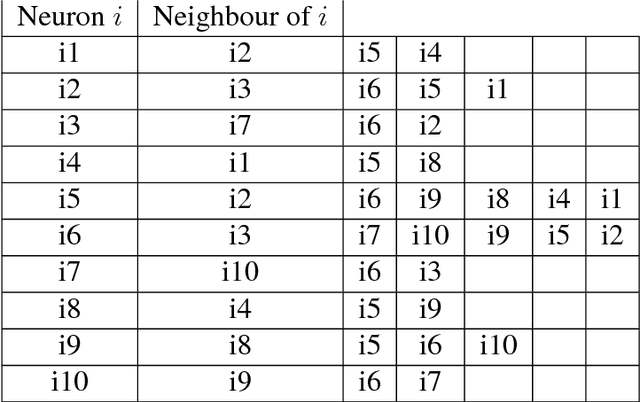
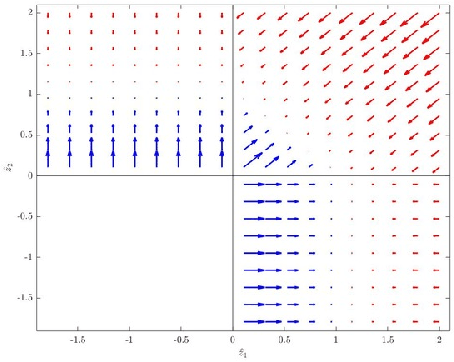
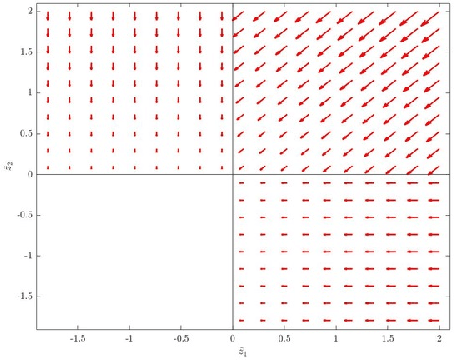
We discuss technical results on learning function approximations using piecewise-linear basis functions, and analyze their stability and convergence using nonlinear contraction theory.