Winfried Lohmiller
MinMax Networks
Jun 15, 2023



Abstract:While much progress has been achieved over the last decades in neuro-inspired machine learning, there are still fundamental theoretical problems in gradient-based learning using combinations of neurons. These problems, such as saddle points and suboptimal plateaus of the cost function, can lead in theory and practice to failures of learning. In addition, the discrete step size selection of the gradient is problematic since too large steps can lead to instability and too small steps slow down the learning. This paper describes an alternative discrete MinMax learning approach for continuous piece-wise linear functions. Global exponential convergence of the algorithm is established using Contraction Theory with Inequality Constraints, which is extended from the continuous to the discrete case in this paper: The parametrization of each linear function piece is, in contrast to deep learning, linear in the proposed MinMax network. This allows a linear regression stability proof as long as measurements do not transit from one linear region to its neighbouring linear region. The step size of the discrete gradient descent is Lagrangian limited orthogonal to the edge of two neighbouring linear functions. It will be shown that this Lagrangian step limitation does not decrease the convergence of the unconstrained system dynamics in contrast to a step size limitation in the direction of the gradient. We show that the convergence rate of a constrained piece-wise linear function learning is equivalent to the exponential convergence rates of the individual local linear regions.
Notes on stable learning with piecewise-linear basis functions
Apr 25, 2018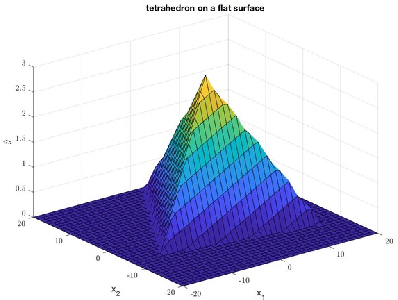
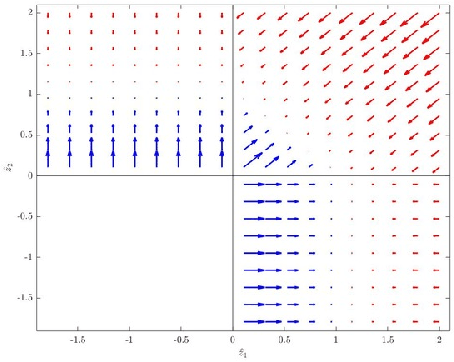
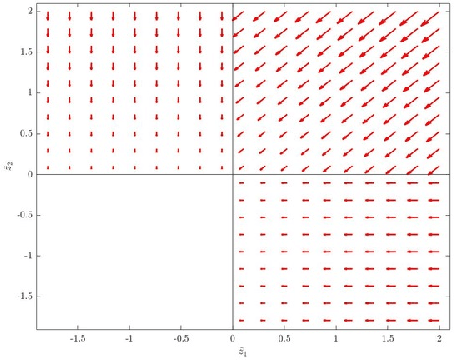
Abstract:We discuss technical results on learning function approximations using piecewise-linear basis functions, and analyze their stability and convergence using nonlinear contraction theory.
Analytical SLAM Without Linearization
Dec 29, 2016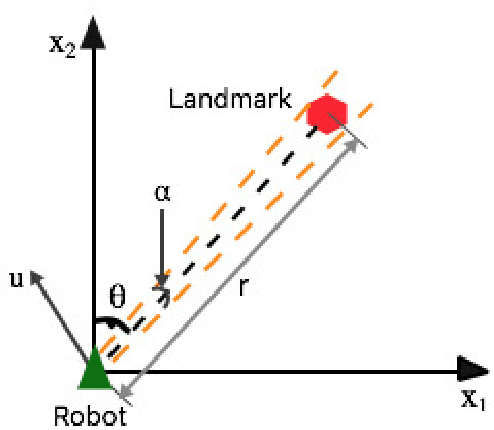
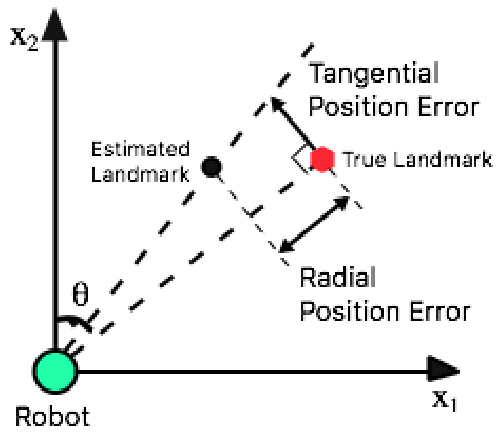
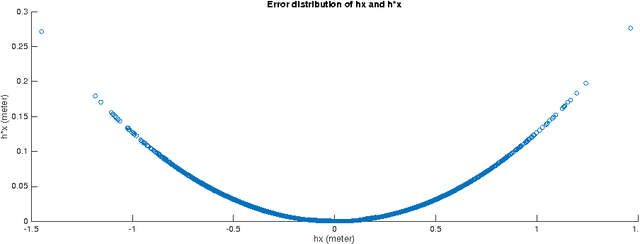
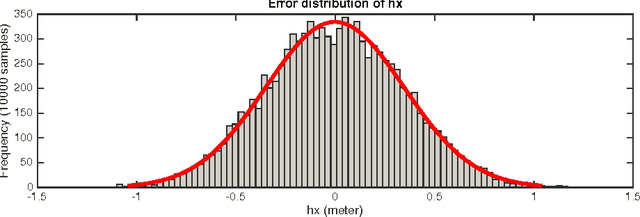
Abstract:This paper solves the classical problem of simultaneous localization and mapping (SLAM) in a fashion which avoids linearized approximations altogether. Based on creating virtual synthetic measurements, the algorithm uses a linear time- varying (LTV) Kalman observer, bypassing errors and approximations brought by the linearization process in traditional extended Kalman filtering (EKF) SLAM. Convergence rates of the algorithm are established using contraction analysis. Different combinations of sensor information can be exploited, such as bearing measurements, range measurements, optical flow, or time-to-contact. As illustrated in simulations, the proposed algorithm can solve SLAM problems in both 2D and 3D scenarios with guaranteed convergence rates in a full nonlinear context.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge