Stable Modular Control via Contraction Theory for Reinforcement Learning

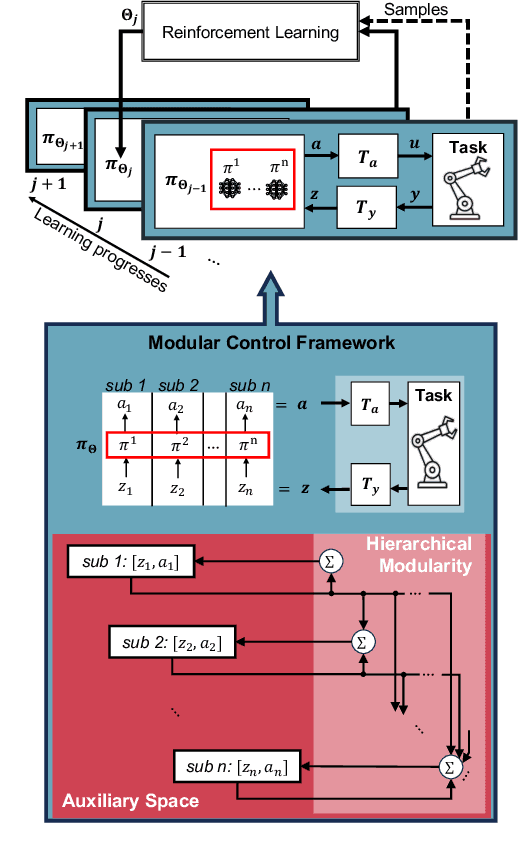
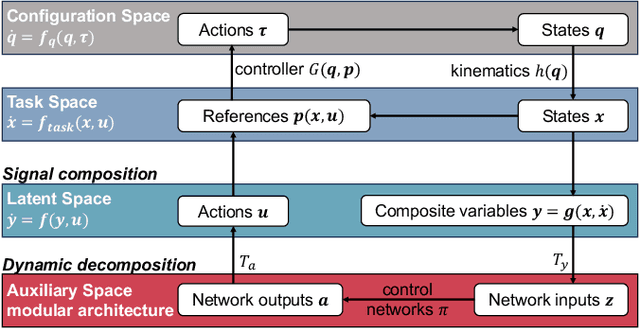
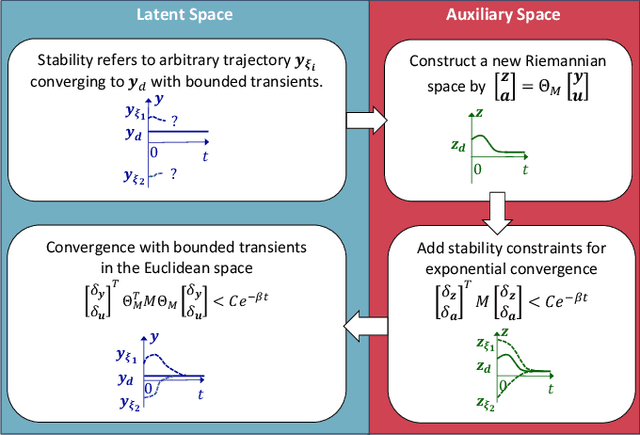
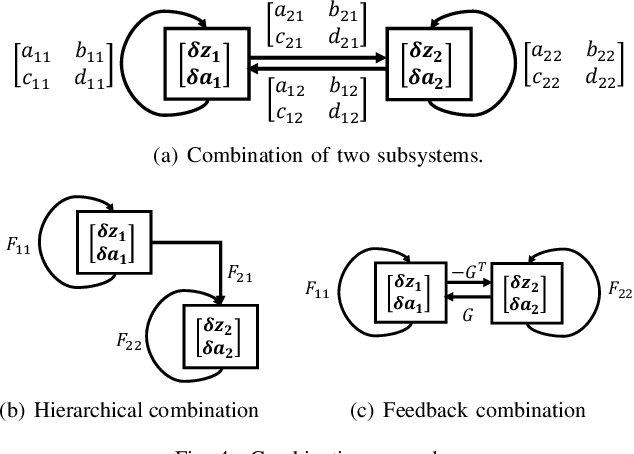
We propose a novel way to integrate control techniques with reinforcement learning (RL) for stability, robustness, and generalization: leveraging contraction theory to realize modularity in neural control, which ensures that combining stable subsystems can automatically preserve the stability. We realize such modularity via signal composition and dynamic decomposition. Signal composition creates the latent space, within which RL applies to maximizing rewards. Dynamic decomposition is realized by coordinate transformation that creates an auxiliary space, within which the latent signals are coupled in the way that their combination can preserve stability provided each signal, that is, each subsystem, has stable self-feedbacks. Leveraging modularity, the nonlinear stability problem is deconstructed into algebraically solvable ones, the stability of the subsystems in the auxiliary space, yielding linear constraints on the input gradients of control networks that can be as simple as switching the signs of network weights. This minimally invasive method for stability allows arguably easy integration into the modular neural architectures in machine learning, like hierarchical RL, and improves their performance. We demonstrate in simulation the necessity and the effectiveness of our method: the necessity for robustness and generalization, and the effectiveness in improving hierarchical RL for manipulation learning.

Stability Guarantees for Continuous RL Control

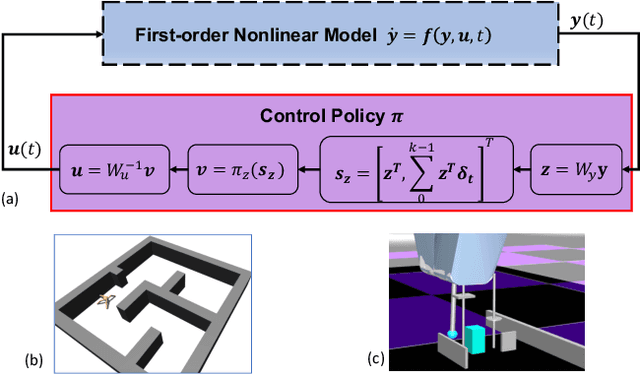
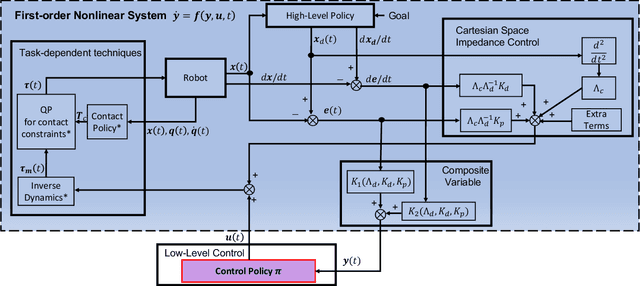
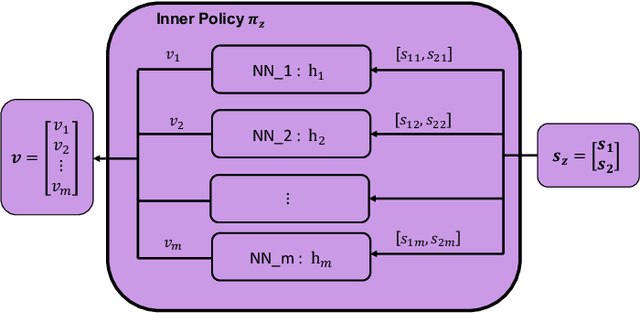
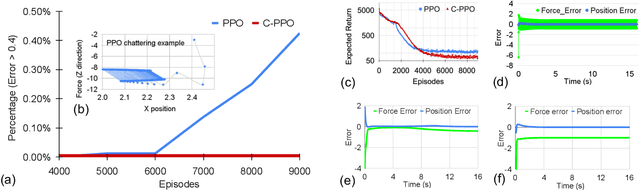
Lack of stability guarantees strongly limits the use of reinforcement learning (RL) in safety critical robotic applications. Here we propose a control system architecture for continuous RL control and derive corresponding stability theorems via contraction analysis, yielding constraints on the network weights to ensure stability. The control architecture can be implemented in general RL algorithms and improve their stability, robustness, and sample efficiency. We demonstrate the importance and benefits of such guarantees for RL on two standard examples, PPO learning of a 2D problem and HIRO learning of maze tasks.

Automatic Snake Gait Generation Using Model Predictive Control

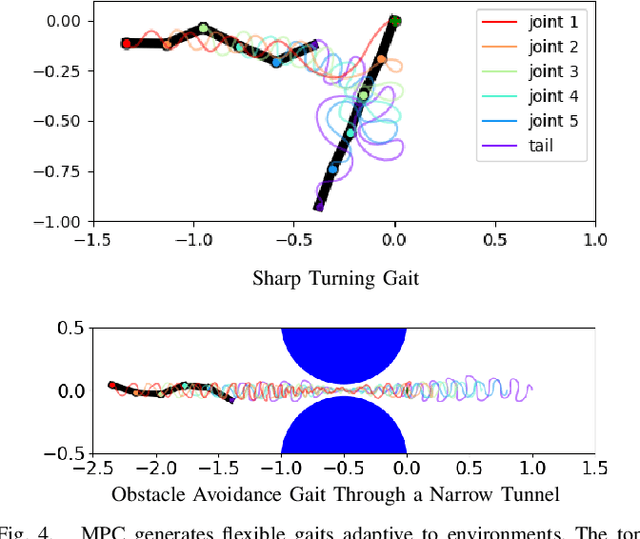
In this paper, we propose a method for generating undulatory gaits for snake robots. Instead of starting from a pre-defined movement pattern such as a serpenoid curve, we use a Model Predictive Control approach to automatically generate effective locomotion gaits via trajectory optimization. An important advantage of this approach is that the resulting gaits are automatically adapted to the environment that is being modeled as part of the snake dynamics. To illustrate this, we use a novel model for anisotropic dry friction, along with existing models for viscous friction and fluid dynamic effects such as drag and added mass. For each of these models, gaits generated without any change in the method or its parameters are as efficient as Pareto-optimal serpenoid gaits tuned individually for each environment. Furthermore, the proposed method can also produce more complex or irregular gaits, e.g. for obstacle avoidance or executing sharp turns.