Lane-Level Route Planning for Autonomous Vehicles

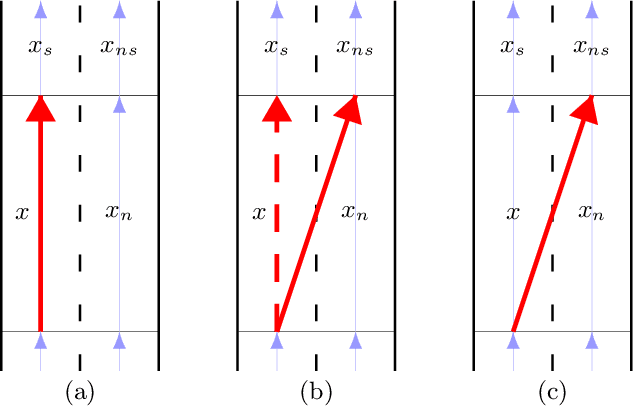
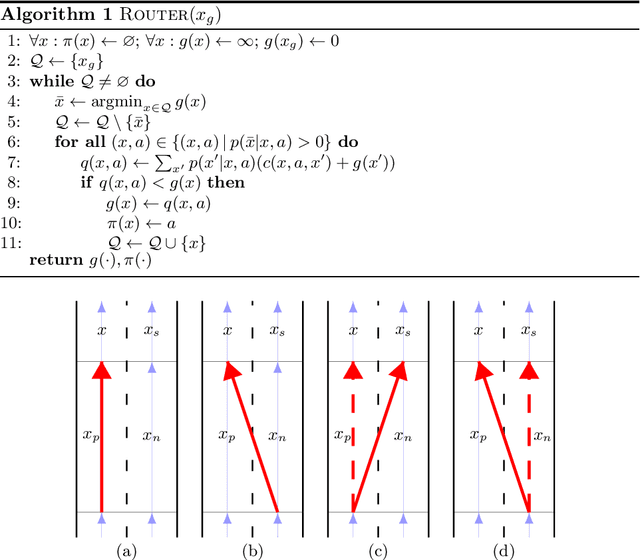
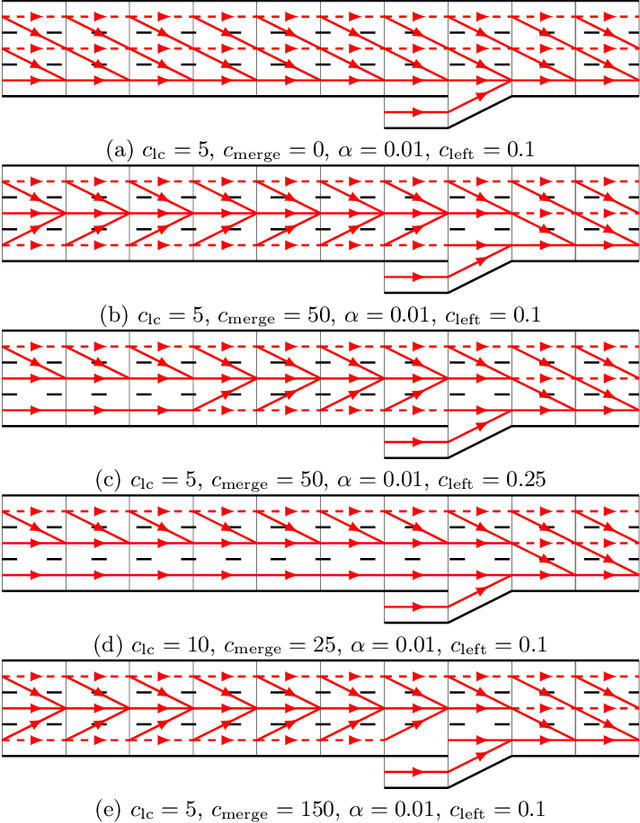
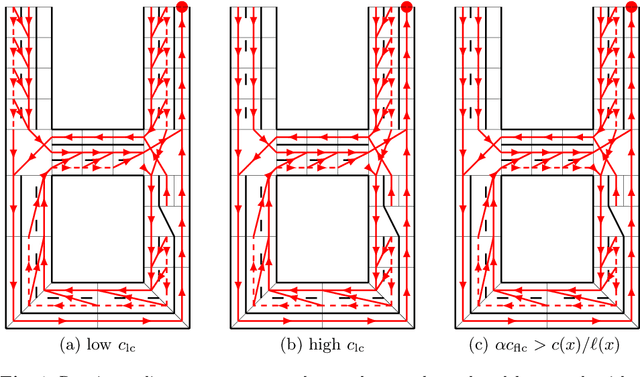
We present an algorithm that, given a representation of a road network in lane-level detail, computes a route that minimizes the expected cost to reach a given destination. In doing so, our algorithm allows us to solve for the complex trade-offs encountered when trying to decide not just which roads to follow, but also when to change between the lanes making up these roads, in order to -- for example -- reduce the likelihood of missing a left exit while not unnecessarily driving in the leftmost lane. This routing problem can naturally be formulated as a Markov Decision Process (MDP), in which lane change actions have stochastic outcomes. However, MDPs are known to be time-consuming to solve in general. In this paper, we show that -- under reasonable assumptions -- we can use a Dijkstra-like approach to solve this stochastic problem, and benefit from its efficient $O(n \log n)$ running time. This enables an autonomous vehicle to exhibit natural lane-selection behavior as it efficiently plans an optimal route to its destination.

Grasp Stability Analysis with Passive Reactions

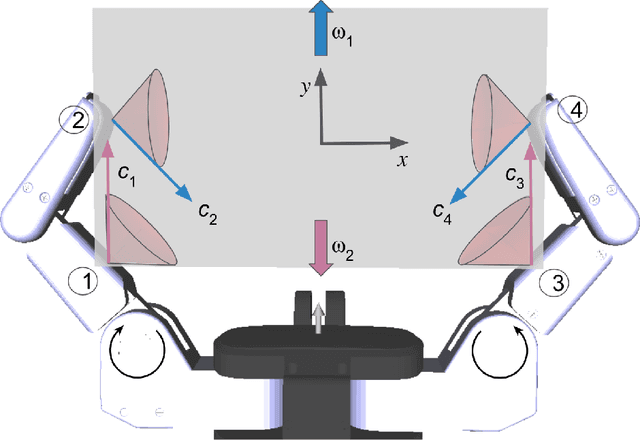
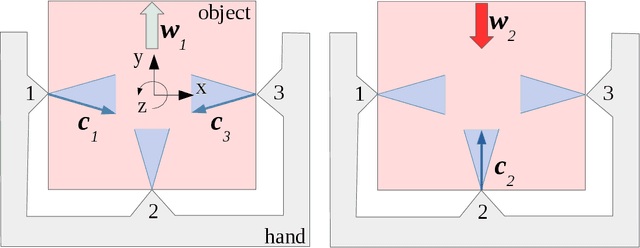
[...] We argue that the traditional grasp modeling theory assumes a complexity that most robotic hands do not possess and is therefore of limited applicability to the robotic hands commonly used today. We discuss these limitations of the existing grasp modeling literature and set out to develop our own tools for the analysis of passive effects in robotic grasping. We show that problems of this kind are difficult to solve due to the non-convexity of the Maximum Dissipation Principle (MDP), which is part of the Coulomb friction law. We show that for planar grasps the MDP can be decomposed into a number of piecewise convex problems, which can be solved for efficiently. [...] Thus, we present the first polynomial runtime algorithm for the determination of passive stability of planar grasps. For the spacial case we [...] describe a convex relaxation of the Coulomb friction law and a successive hierarchical tightening approach that allows us to find solutions to the exact problem including the maximum dissipation principle. [...] The generality of our grasp model allows us to solve a wide variety of problems such as the computation of optimal actuator commands. This makes our framework a valuable tool for practical manipulation applications. Our work is relevant beyond robotic manipulation as it applies to the stability of any assembly of rigid bodies with frictional contacts, unilateral constraints and externally applied wrenches. Finally, we argue that with the advent of data-driven methods as well as the emergence of a new generation of highly sensorized hands there are opportunities for the application of the traditional grasp modeling theory to fields such as robotic in-hand manipulation through model-free reinforcement learning. We present a method that applies traditional grasp models to maintain quasi-static stability throughout a nominally model-free reinforcement learning task. [...]

A Continuous Teleoperation Subspace with Empirical and Algorithmic Mapping Algorithms for Non-Anthropomorphic Hands

Teleoperation is a valuable tool for robotic manipulators in highly unstructured environments. However, finding an intuitive mapping between a human hand and a non-anthropomorphic robot hand can be difficult, due to the hands' dissimilar kinematics. In this paper, we seek to create a mapping between the human hand and a fully actuated, non-anthropomorphic robot hand that is intuitive enough to enable effective real-time teleoperation, even for novice users. To accomplish this, we propose a low-dimensional teleoperation subspace which can be used as an intermediary for mapping between hand pose spaces. We present two different methods to define the teleoperation subspace: an empirical definition, which requires a person to define hand motions in an intuitive, hand-specific way, and an algorithmic definition, which is kinematically independent, and uses objects to define the subspace. We use each of these definitions to create a teleoperation mapping for different hands. We validate both the empirical and algorithmic mappings with teleoperation experiments controlled by novices and performed on two kinematically distinct hands. The experiments show that the proposed subspace is relevant to teleoperation, intuitive enough to enable control by novices, and can generalize to non-anthropomorphic hands with different kinematic configurations.

Automatic Snake Gait Generation Using Model Predictive Control

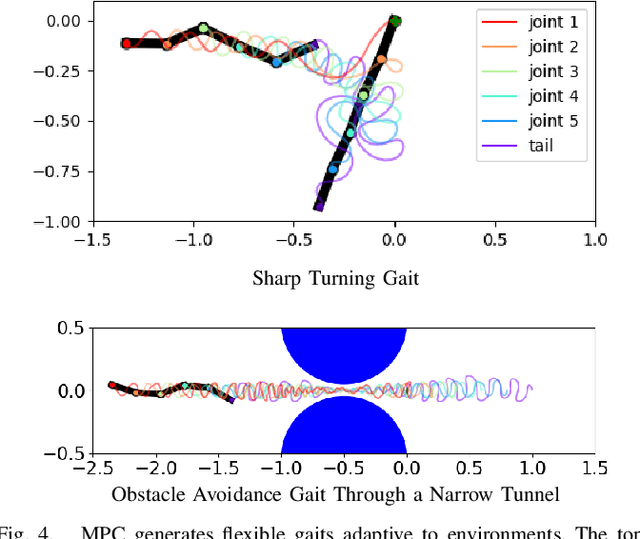
In this paper, we propose a method for generating undulatory gaits for snake robots. Instead of starting from a pre-defined movement pattern such as a serpenoid curve, we use a Model Predictive Control approach to automatically generate effective locomotion gaits via trajectory optimization. An important advantage of this approach is that the resulting gaits are automatically adapted to the environment that is being modeled as part of the snake dynamics. To illustrate this, we use a novel model for anisotropic dry friction, along with existing models for viscous friction and fluid dynamic effects such as drag and added mass. For each of these models, gaits generated without any change in the method or its parameters are as efficient as Pareto-optimal serpenoid gaits tuned individually for each environment. Furthermore, the proposed method can also produce more complex or irregular gaits, e.g. for obstacle avoidance or executing sharp turns.

3D Grasp Stability Analysis with Coulomb Friction with Hierarchical Convex Relaxations

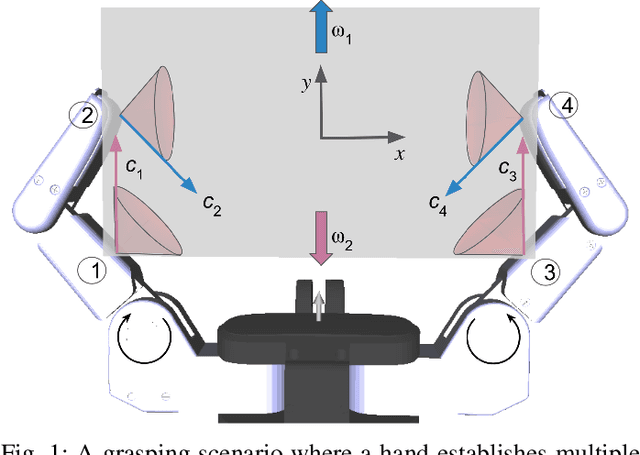
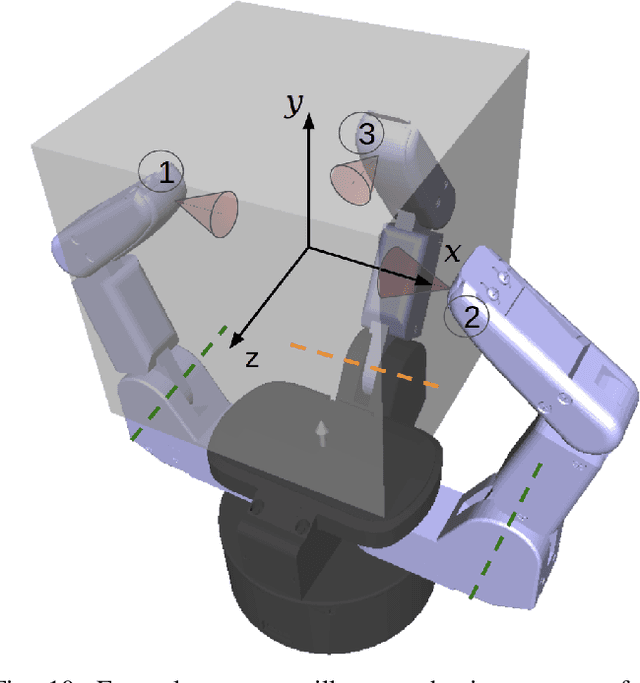
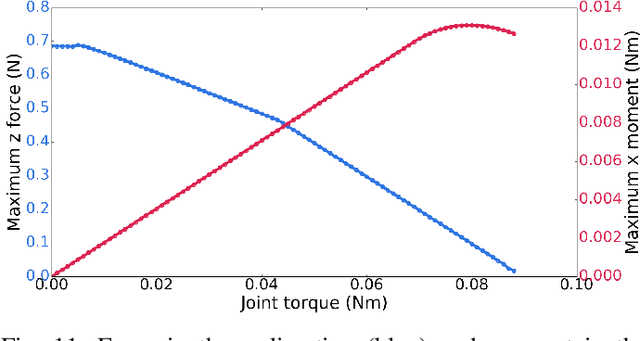
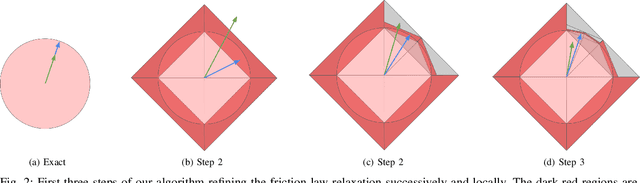
We present an algorithm to determine quasistatic equilibrium of three dimensional grasps in the presence of Coulomb Friction. Due to the non-convexity of this friction law we introduce a relaxation that allows us to formulate the problem as a Mixed-Integer Problem. This type of problem can be solved efficiently with methods such as the branch and bound algorithm. However, as the number of integer variables will greatly affect computation time we present an algorithm that successively refines the friction constraint relaxation locally to obtain solutions to arbitrary accuracy efficiently. This allows us to determine if a system is quasistatically stable (i.e. it is in equilibrium) or not. Furthermore, we can solve for the equilibrium contact forces or actuator commands necessary for stability. We apply this algorithm to analyze the conditions for stability of robotic grasps.

Underactuated Hand Design Using Mechanically Realizable Manifolds

Hand synergies, or joint coordination patterns, have become an effective tool for achieving versatile robotic grasping with simple hands or planning algorithms. Here we propose a method to determine the hand synergies such that they can be physically implemented in an underactuated fashion. Given a kinematic hand model and a set of desired grasps, our algorithm optimizes a Mechanically Realizable Manifold designed to be achievable by a physical underactuation mechanism, enabling the resulting hand to achieve the desired grasps with few actuators. Furthermore, in contrast to existing methods for determining synergies which are only concerned with hand posture, our method explicitly optimizes the stability of the target grasps. We implement this method in the design of a three-finger single-actuator hand as an example, and evaluate its effectiveness numerically and experimentally.

Passive Static Equilibrium with Frictional Contacts and Application to Grasp Stability Analysis

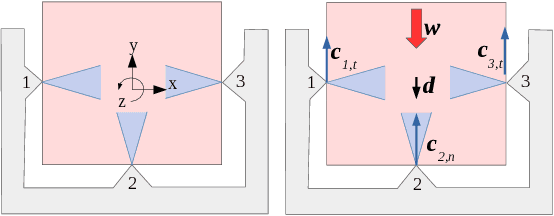
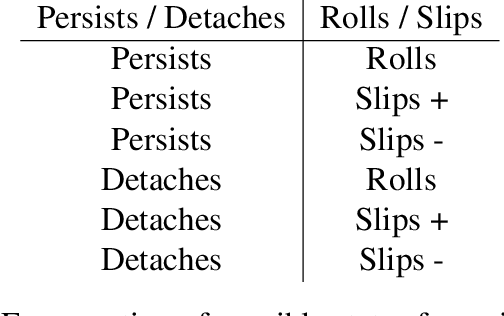
This paper studies the problem of passive grasp stability under an external disturbance, that is, the ability of a grasp to resist a disturbance through passive responses at the contacts. To obtain physically consistent results, such a model must account for friction phenomena at each contact; the difficulty is that friction forces depend in non-linear fashion on contact behavior (stick or slip). We develop the first polynomial-time algorithm which either solves such complex equilibrium constraints for two-dimensional grasps, or otherwise concludes that no solution exists. To achieve this, we show that the number of possible `slip states' (where each contact is labeled as either sticking or slipping) that must be considered is polynomial (in fact quadratic) in the number of contacts, and not exponential as previously thought. Our algorithm captures passive response behaviors at each contact, while accounting for constraints on friction forces such as the maximum dissipation principle.

Passive Reaction Analysis for Grasp Stability

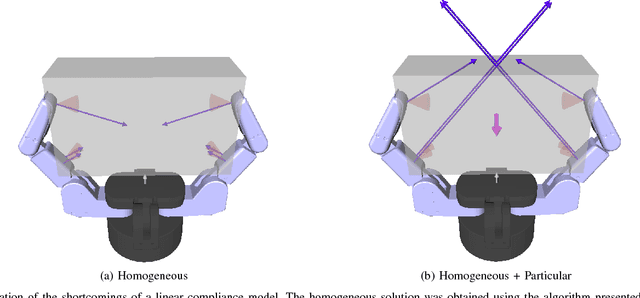
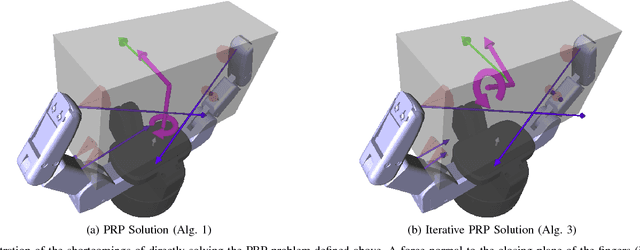
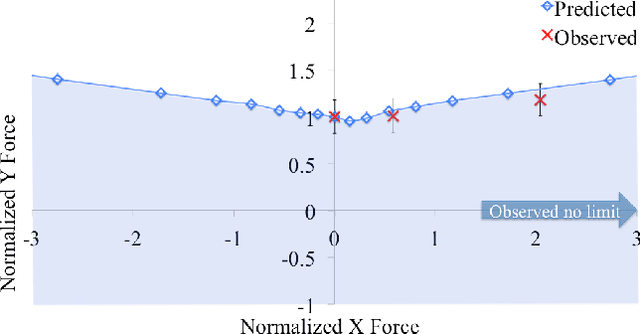
In this paper we focus on the following problem in multi-fingered robotic grasping: assuming that an external wrench is being applied to a grasped object, will the contact forces between the hand and the object, as well as the hand joints, respond in such a way as to preserve quasi-static equilibrium? In particular, we assume that there is no change in the joint torques being actively exerted by the motors; any change in contact forces and joint torques is due exclusively to passive effects arising in response to the external disturbance. Such passive effects include for example joints that are driven by highly geared motors (a common occurence in practice) and thus do not back drive in response to external torques. To account for non- linear phenomena encountered in such cases, and which existing methods do not consider, we formulate the problem as a mixed integer program used in the inner loop of an iterative solver. We present evidence showing that this formulation captures important effects for assessing the stability of a grasp employing some of the most commonly used actuation mechanisms.