Passive Static Equilibrium with Frictional Contacts and Application to Grasp Stability Analysis
Paper and Code
Jun 13, 2018

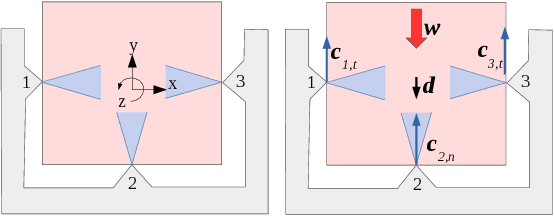

This paper studies the problem of passive grasp stability under an external disturbance, that is, the ability of a grasp to resist a disturbance through passive responses at the contacts. To obtain physically consistent results, such a model must account for friction phenomena at each contact; the difficulty is that friction forces depend in non-linear fashion on contact behavior (stick or slip). We develop the first polynomial-time algorithm which either solves such complex equilibrium constraints for two-dimensional grasps, or otherwise concludes that no solution exists. To achieve this, we show that the number of possible `slip states' (where each contact is labeled as either sticking or slipping) that must be considered is polynomial (in fact quadratic) in the number of contacts, and not exponential as previously thought. Our algorithm captures passive response behaviors at each contact, while accounting for constraints on friction forces such as the maximum dissipation principle.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge