Lane-Level Route Planning for Autonomous Vehicles

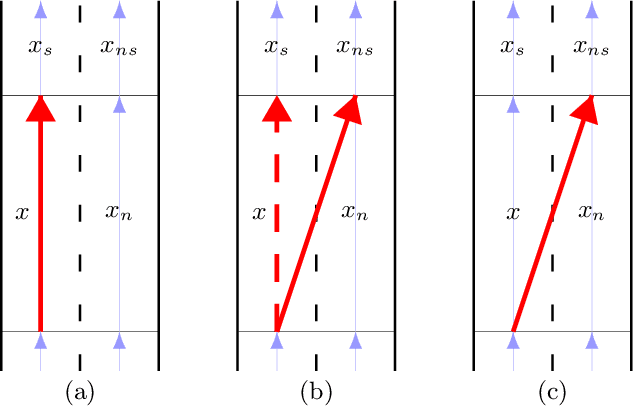
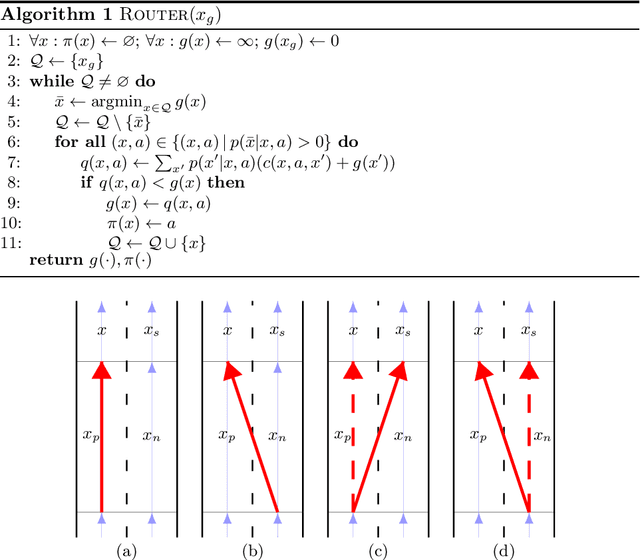
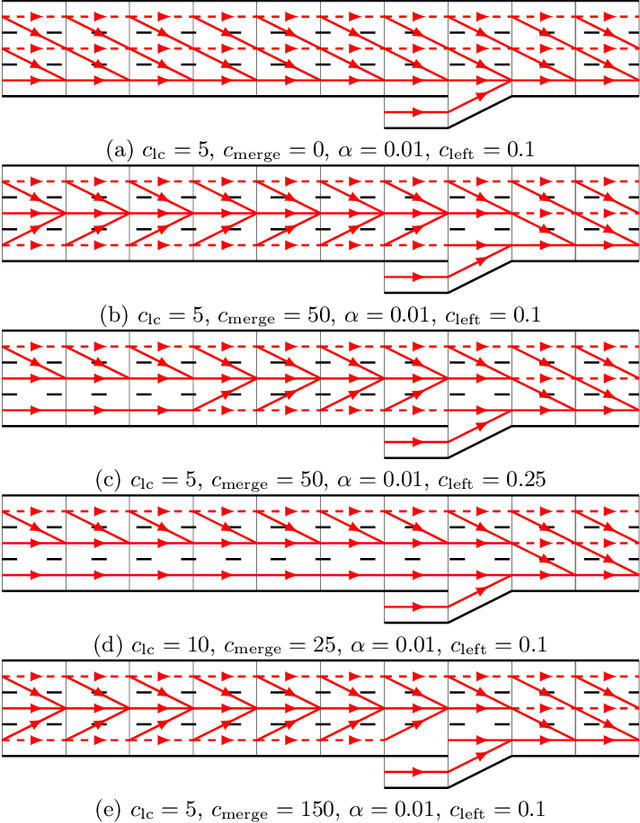
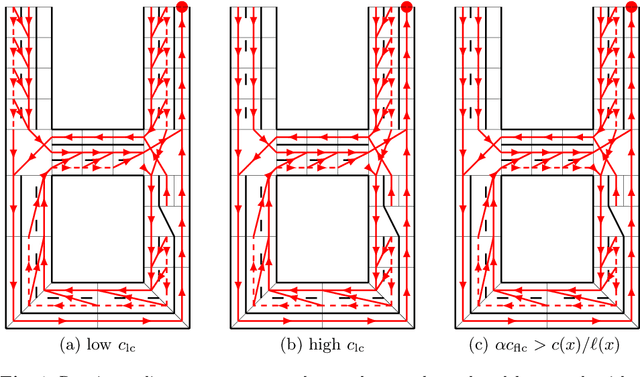
We present an algorithm that, given a representation of a road network in lane-level detail, computes a route that minimizes the expected cost to reach a given destination. In doing so, our algorithm allows us to solve for the complex trade-offs encountered when trying to decide not just which roads to follow, but also when to change between the lanes making up these roads, in order to -- for example -- reduce the likelihood of missing a left exit while not unnecessarily driving in the leftmost lane. This routing problem can naturally be formulated as a Markov Decision Process (MDP), in which lane change actions have stochastic outcomes. However, MDPs are known to be time-consuming to solve in general. In this paper, we show that -- under reasonable assumptions -- we can use a Dijkstra-like approach to solve this stochastic problem, and benefit from its efficient $O(n \log n)$ running time. This enables an autonomous vehicle to exhibit natural lane-selection behavior as it efficiently plans an optimal route to its destination.

3-D Reciprocal Collision Avoidance on Physical Quadrotor Helicopters with On-Board Sensing for Relative Positioning

In this paper, we present an implementation of 3-D reciprocal collision avoidance on real quadrotor helicopters where each quadrotor senses the relative position and velocity of other quadrotors using an on-board camera. We show that using our approach, quadrotors are able to successfully avoid pairwise collisions in GPS and motion-capture denied environments, without communication between the quadrotors, and even when human operators deliberately attempt to induce collisions. To our knowledge, this is the first time that reciprocal collision avoidance has been successfully implemented on real robots where each agent independently observes the others using on-board sensors. We theoretically analyze the response of the collision-avoidance algorithm to the violated assumptions by the use of real robots. We quantitatively analyze our experimental results. A particularly striking observation is that at times the quadrotors exhibit "reciprocal dance" behavior, which is also observed when humans move past each other in constrained environments. This seems to be the result of sensing uncertainty, which causes both robots involved to have a different belief about the relative positions and velocities and, as a result, choose the same side on which to pass.

Kinodynamic RRT*: Optimal Motion Planning for Systems with Linear Differential Constraints

We present Kinodynamic RRT*, an incremental sampling-based approach for asymptotically optimal motion planning for robots with linear differential constraints. Our approach extends RRT*, which was introduced for holonomic robots (Karaman et al. 2011), by using a fixed-final-state-free-final-time controller that exactly and optimally connects any pair of states, where the cost function is expressed as a trade-off between the duration of a trajectory and the expended control effort. Our approach generalizes earlier work on extending RRT* to kinodynamic systems, as it guarantees asymptotic optimality for any system with controllable linear dynamics, in state spaces of any dimension. Our approach can be applied to non-linear dynamics as well by using their first-order Taylor approximations. In addition, we show that for the rich subclass of systems with a nilpotent dynamics matrix, closed-form solutions for optimal trajectories can be derived, which keeps the computational overhead of our algorithm compared to traditional RRT* at a minimum. We demonstrate the potential of our approach by computing asymptotically optimal trajectories in three challenging motion planning scenarios: (i) a planar robot with a 4-D state space and double integrator dynamics, (ii) an aerial vehicle with a 10-D state space and linearized quadrotor dynamics, and (iii) a car-like robot with a 5-D state space and non-linear dynamics.