3D Grasp Stability Analysis with Coulomb Friction with Hierarchical Convex Relaxations

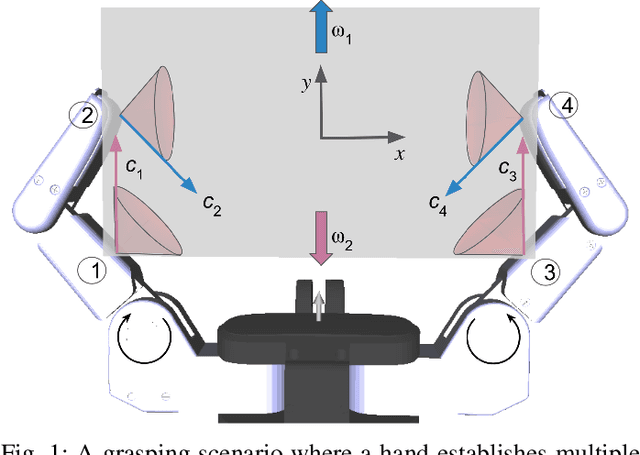
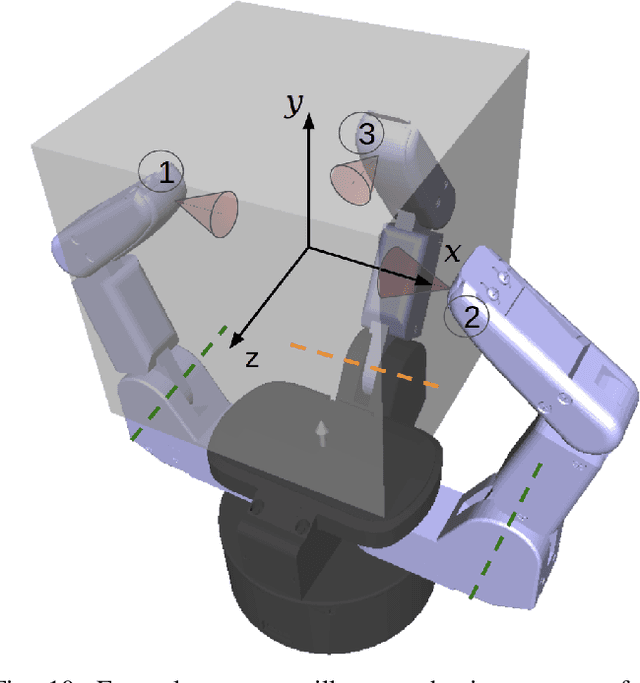
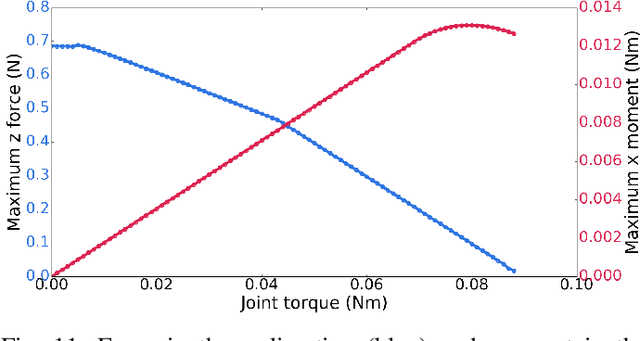
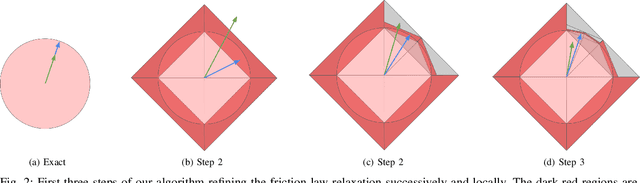
We present an algorithm to determine quasistatic equilibrium of three dimensional grasps in the presence of Coulomb Friction. Due to the non-convexity of this friction law we introduce a relaxation that allows us to formulate the problem as a Mixed-Integer Problem. This type of problem can be solved efficiently with methods such as the branch and bound algorithm. However, as the number of integer variables will greatly affect computation time we present an algorithm that successively refines the friction constraint relaxation locally to obtain solutions to arbitrary accuracy efficiently. This allows us to determine if a system is quasistatically stable (i.e. it is in equilibrium) or not. Furthermore, we can solve for the equilibrium contact forces or actuator commands necessary for stability. We apply this algorithm to analyze the conditions for stability of robotic grasps.