Stable Modular Control via Contraction Theory for Reinforcement Learning

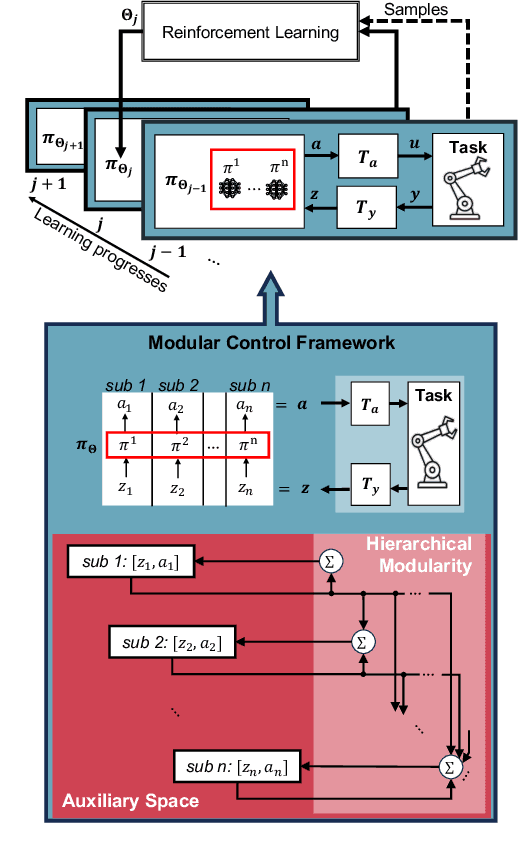
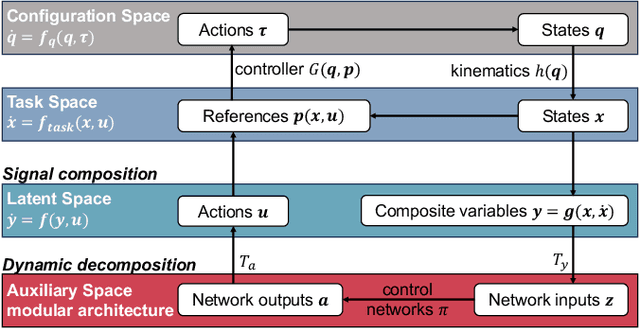
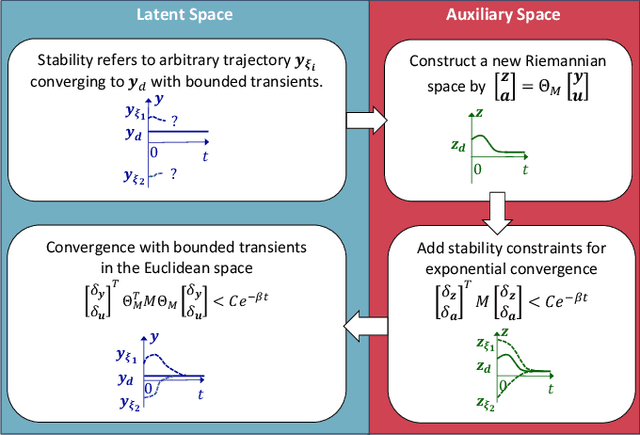
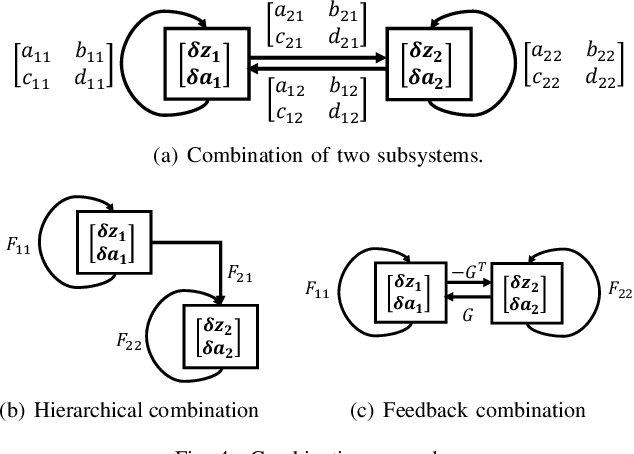
We propose a novel way to integrate control techniques with reinforcement learning (RL) for stability, robustness, and generalization: leveraging contraction theory to realize modularity in neural control, which ensures that combining stable subsystems can automatically preserve the stability. We realize such modularity via signal composition and dynamic decomposition. Signal composition creates the latent space, within which RL applies to maximizing rewards. Dynamic decomposition is realized by coordinate transformation that creates an auxiliary space, within which the latent signals are coupled in the way that their combination can preserve stability provided each signal, that is, each subsystem, has stable self-feedbacks. Leveraging modularity, the nonlinear stability problem is deconstructed into algebraically solvable ones, the stability of the subsystems in the auxiliary space, yielding linear constraints on the input gradients of control networks that can be as simple as switching the signs of network weights. This minimally invasive method for stability allows arguably easy integration into the modular neural architectures in machine learning, like hierarchical RL, and improves their performance. We demonstrate in simulation the necessity and the effectiveness of our method: the necessity for robustness and generalization, and the effectiveness in improving hierarchical RL for manipulation learning.