Contraction Theory for Nonlinear Stability Analysis and Learning-based Control: A Tutorial Overview
Paper and Code
Oct 01, 2021
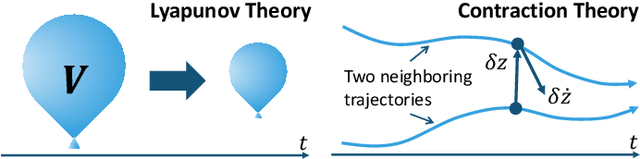


Contraction theory is an analytical tool to study differential dynamics of a non-autonomous (i.e., time-varying) nonlinear system under a contraction metric defined with a uniformly positive definite matrix, the existence of which results in a necessary and sufficient characterization of incremental exponential stability of multiple solution trajectories with respect to each other. By using a squared differential length as a Lyapunov-like function, its nonlinear stability analysis boils down to finding a suitable contraction metric that satisfies a stability condition expressed as a linear matrix inequality, indicating that many parallels can be drawn between well-known linear systems theory and contraction theory for nonlinear systems. Furthermore, contraction theory takes advantage of a superior robustness property of exponential stability used in conjunction with the comparison lemma. This yields much-needed safety and stability guarantees for neural network-based control and estimation schemes, without resorting to a more involved method of using uniform asymptotic stability for input-to-state stability. Such distinctive features permit systematic construction of a contraction metric via convex optimization, thereby obtaining an explicit exponential bound on the distance between a time-varying target trajectory and solution trajectories perturbed externally due to disturbances and learning errors. The objective of this paper is therefore to present a tutorial overview of contraction theory and its advantages in nonlinear stability analysis of deterministic and stochastic systems, with an emphasis on deriving formal robustness and stability guarantees for various learning-based and data-driven automatic control methods. In particular, we provide a detailed review of techniques for finding contraction metrics and associated control and estimation laws using deep neural networks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge