Nonlinear Controller Design for a Quadrotor with Inverted Pendulum

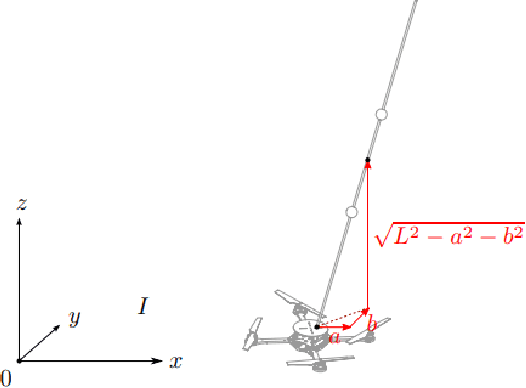
The quadrotor is a $6$ degrees-of-freedom (DoF) system with underactuation. Adding a spherical pendulum on top of a quadrotor further complicates the task of achieving any output tracking while stabilizing the rest. In this report, we present different types of controllers for the nonlinear dynamical system of quadrotor and pendulum combination, utilizing feedback-linearization and control Lyapunov function with quadratic programming (CLF-QP) approaches. We demonstrated trajectory tracking for quadrotor-only case as well as quadrotor-pendulum-combined case.

Neural-Rendezvous: Learning-based Robust Guidance and Control to Encounter Interstellar Objects

Interstellar objects (ISOs), astronomical objects not gravitationally bound to the Sun, are likely representatives of primitive materials invaluable in understanding exoplanetary star systems. Due to their poorly constrained orbits with generally high inclinations and relative velocities, however, exploring ISOs with conventional human-in-the-loop approaches is significantly challenging. This paper presents Neural-Rendezvous -- a deep learning-based guidance and control framework for encountering any fast-moving objects, including ISOs, robustly, accurately, and autonomously in real-time. It uses pointwise minimum norm tracking control on top of a guidance policy modeled by a spectrally-normalized deep neural network, where its hyperparameters are tuned with a newly introduced loss function directly penalizing the state trajectory tracking error. We rigorously show that, even in the challenging case of ISO exploration, Neural-Rendezvous provides 1) a high probability exponential bound on the expected spacecraft delivery error; and 2) a finite optimality gap with respect to the solution of model predictive control, both of which are indispensable especially for such a critical space mission. In numerical simulations, Neural-Rendezvous is demonstrated to achieve a terminal-time delivery error of less than 0.2 km for 99% of the ISO candidates with realistic state uncertainty, whilst retaining computational efficiency sufficient for real-time implementation.

Learning-based methods to model small body gravity fields for proximity operations: Safety and Robustness

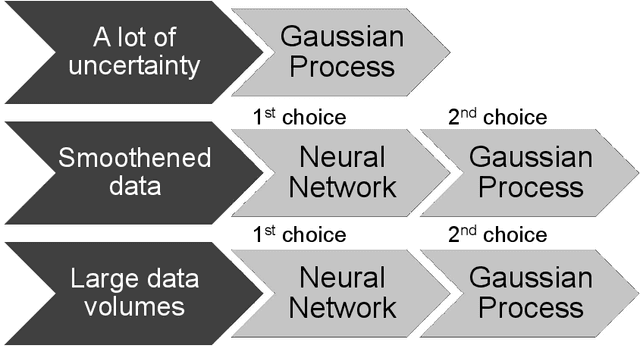
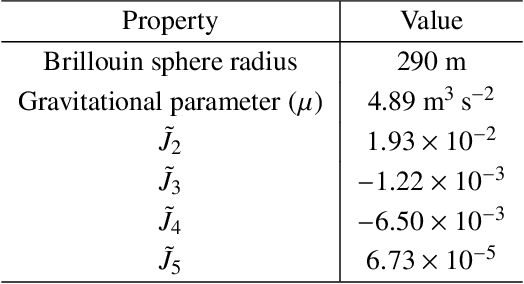
Accurate gravity field models are essential for safe proximity operations around small bodies. State-of-the-art techniques use spherical harmonics or high-fidelity polyhedron shape models. Unfortunately, these techniques can become inaccurate near the surface of the small body or have high computational costs, especially for binary or heterogeneous small bodies. New learning-based techniques do not encode a predefined structure and are more versatile. In exchange for versatility, learning-based techniques can be less robust outside the training data domain. In deployment, the spacecraft trajectory is the primary source of dynamics data. Therefore, the training data domain should include spacecraft trajectories to accurately evaluate the learned model's safety and robustness. We have developed a novel method for learning-based gravity models that directly uses the spacecraft's past trajectories. We further introduce a method to evaluate the safety and robustness of learning-based techniques via comparing accuracy within and outside of the training domain. We demonstrate this safety and robustness method for two learning-based frameworks: Gaussian processes and neural networks. Along with the detailed analysis provided, we empirically establish the need for robustness verification of learned gravity models when used for proximity operations.

Trajectory Optimization of Chance-Constrained Nonlinear Stochastic Systems for Motion Planning and Control

We present gPC-SCP: Generalized Polynomial Chaos-based Sequential Convex Programming method to compute a sub-optimal solution for a continuous-time chance-constrained stochastic nonlinear optimal control problem (SNOC) problem. The approach enables motion planning and control of robotic systems under uncertainty. The proposed method involves two steps. The first step is to derive a deterministic nonlinear optimal control problem (DNOC) with convex constraints that are surrogate to the SNOC by using gPC expansion and the distributionally-robust convex subset of the chance constraints. The second step is to solve the DNOC problem using sequential convex programming (SCP) for trajectory generation and control. We prove that in the unconstrained case, the optimal value of the DNOC converges to that of SNOC asymptotically and that any feasible solution of the constrained DNOC is a feasible solution of the chance-constrained SNOC. We derive a stable stochastic model predictive controller using the gPC-SCP for tracking a trajectory in the presence of uncertainty. We empirically demonstrate the efficacy of the gPC-SCP method for the following three test cases: 1) collision checking under uncertainty in actuation, 2) collision checking with stochastic obstacle model, and 3) safe trajectory tracking under uncertainty in the dynamics and obstacle location by using a receding horizon control approach. We validate the effectiveness of the gPC-SCP method on the robotic spacecraft testbed.

Chance-Constrained Trajectory Optimization for Safe Exploration and Learning of Nonlinear Systems

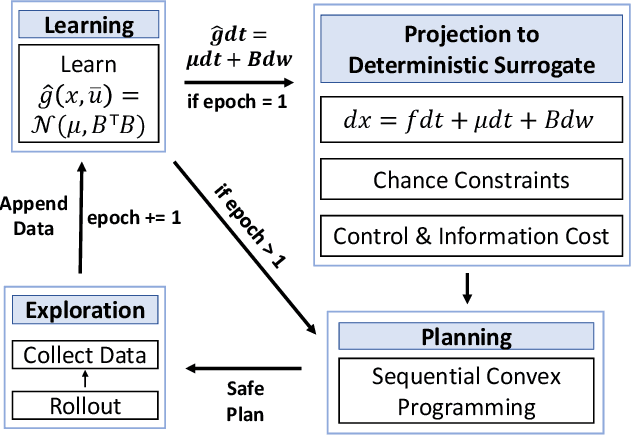
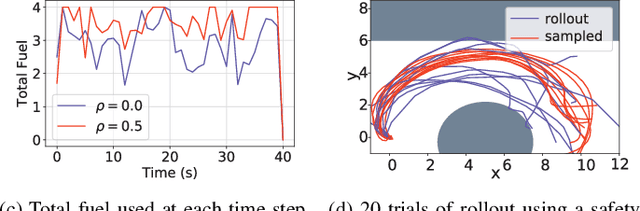
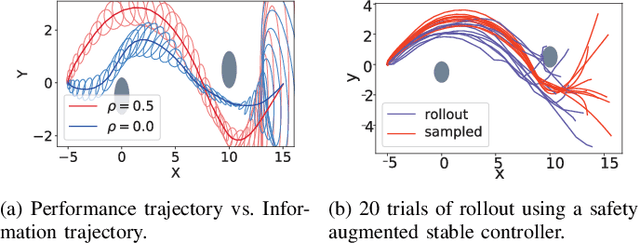
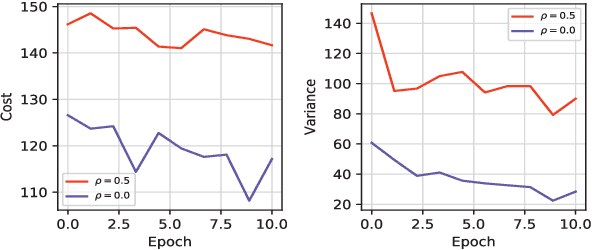
Learning-based control algorithms require collection of abundant supervision for training. Safe exploration algorithms enable this data collection to proceed safely even when only partial knowledge is available. In this paper, we present a new episodic framework to design a sub-optimal pool of motion plans that aid exploration for learning unknown residual dynamics under safety constraints. We derive an iterative convex optimization algorithm that solves an information-cost Stochastic Nonlinear Optimal Control problem (Info-SNOC), subject to chance constraints and approximated dynamics to compute a safe trajectory. The optimization objective encodes both performance and exploration, and the safety is incorporated as distributionally robust chance constraints. The dynamics are predicted from a robust learning model. We prove the safety of rollouts from our exploration method and reduction in uncertainty over epochs ensuring consistency of our learning method. We validate the effectiveness of Info-SNOC by designing and implementing a pool of safe trajectories for a planar robot.