CART: Collision Avoidance and Robust Tracking Augmentation in Learning-based Motion Planning for Multi-Agent Systems
Paper and Code
Jul 13, 2023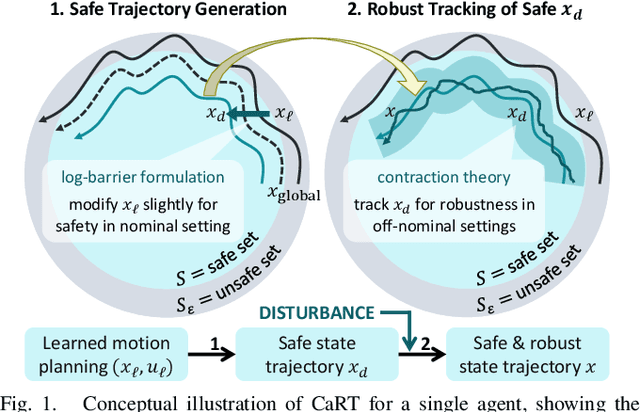
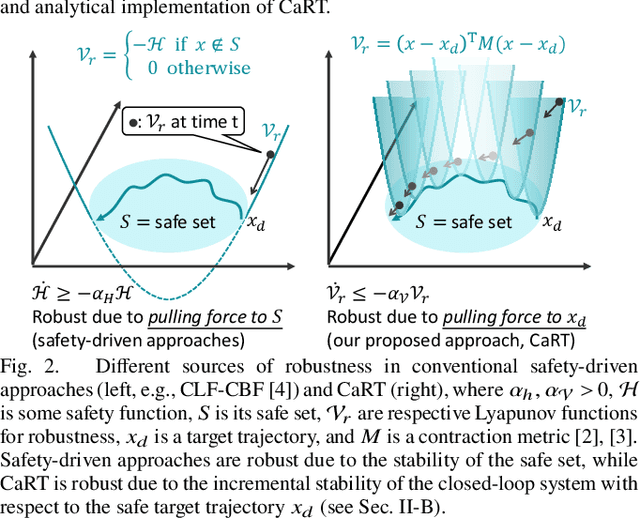
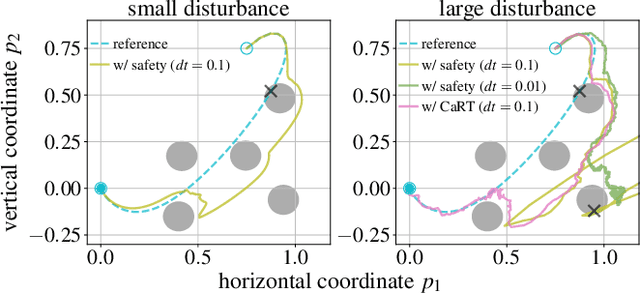

This paper presents CART, an analytical method to augment a learning-based, distributed motion planning policy of a nonlinear multi-agent system with real-time collision avoidance and robust tracking guarantees, independently of learning errors. We first derive an analytical form of an optimal safety filter for Lagrangian systems, which formally ensures a collision-free operation in a multi-agent setting in a disturbance-free environment, while allowing for its distributed implementation with minimal deviation from the learned policy. We then propose an analytical form of an optimal robust filter for Lagrangian systems to be used hierarchically with the learned collision-free target trajectory, which also enables distributed implementation and guarantees exponential boundedness of the trajectory tracking error for safety, even under the presence of deterministic and stochastic disturbance. These results are shown to extend further to general control-affine nonlinear systems using contraction theory. Our key contribution is to enhance the performance of the learned motion planning policy with collision avoidance and tracking-based robustness guarantees, independently of its original performance such as approximation errors and regret bounds in machine learning. We demonstrate the effectiveness of CART in motion planning and control of several examples of nonlinear systems, including spacecraft formation flying and rotor-failed UAV swarms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge