Imitating Complex Trajectories: Bridging Low-Level Stability and High-Level Behavior
Paper and Code
Jul 29, 2023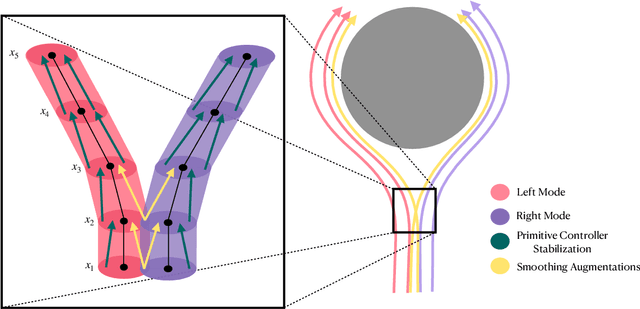


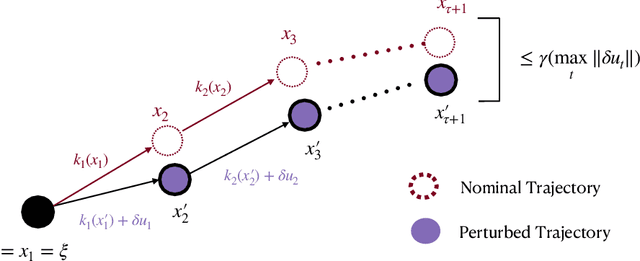
We propose a theoretical framework for studying the imitation of stochastic, non-Markovian, potentially multi-modal (i.e. "complex" ) expert demonstrations in nonlinear dynamical systems. Our framework invokes low-level controllers - either learned or implicit in position-command control - to stabilize imitation policies around expert demonstrations. We show that with (a) a suitable low-level stability guarantee and (b) a stochastic continuity property of the learned policy we call "total variation continuity" (TVC), an imitator that accurately estimates actions on the demonstrator's state distribution closely matches the demonstrator's distribution over entire trajectories. We then show that TVC can be ensured with minimal degradation of accuracy by combining a popular data-augmentation regimen with a novel algorithmic trick: adding augmentation noise at execution time. We instantiate our guarantees for policies parameterized by diffusion models and prove that if the learner accurately estimates the score of the (noise-augmented) expert policy, then the distribution of imitator trajectories is close to the demonstrator distribution in a natural optimal transport distance. Our analysis constructs intricate couplings between noise-augmented trajectories, a technique that may be of independent interest. We conclude by empirically validating our algorithmic recommendations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge