Transfer learning for improved generalizability in causal physics-informed neural networks for beam simulations

This paper introduces a novel methodology for simulating the dynamics of beams on elastic foundations. Specifically, Euler-Bernoulli and Timoshenko beam models on the Winkler foundation are simulated using a transfer learning approach within a causality-respecting physics-informed neural network (PINN) framework. Conventional PINNs encounter challenges in handling large space-time domains, even for problems with closed-form analytical solutions. A causality-respecting PINN loss function is employed to overcome this limitation, effectively capturing the underlying physics. However, it is observed that the causality-respecting PINN lacks generalizability. We propose using solutions to similar problems instead of training from scratch by employing transfer learning while adhering to causality to accelerate convergence and ensure accurate results across diverse scenarios. Numerical experiments on the Euler-Bernoulli beam highlight the efficacy of the proposed approach for various initial conditions, including those with noise in the initial data. Furthermore, the potential of the proposed method is demonstrated for the Timoshenko beam in an extended spatial and temporal domain. Several comparisons suggest that the proposed method accurately captures the inherent dynamics, outperforming the state-of-the-art physics-informed methods under standard $L^2$-norm metric and accelerating convergence.

Neural oscillators for generalization of physics-informed machine learning

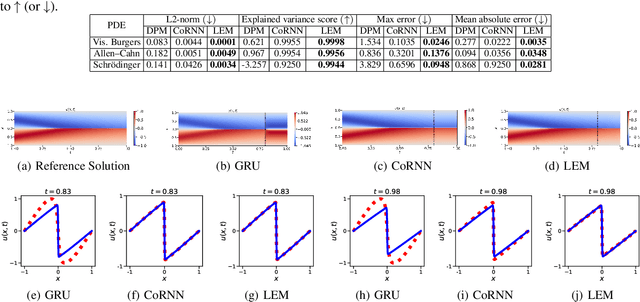
A primary challenge of physics-informed machine learning (PIML) is its generalization beyond the training domain, especially when dealing with complex physical problems represented by partial differential equations (PDEs). This paper aims to enhance the generalization capabilities of PIML, facilitating practical, real-world applications where accurate predictions in unexplored regions are crucial. We leverage the inherent causality and temporal sequential characteristics of PDE solutions to fuse PIML models with recurrent neural architectures based on systems of ordinary differential equations, referred to as neural oscillators. Through effectively capturing long-time dependencies and mitigating the exploding and vanishing gradient problem, neural oscillators foster improved generalization in PIML tasks. Extensive experimentation involving time-dependent nonlinear PDEs and biharmonic beam equations demonstrates the efficacy of the proposed approach. Incorporating neural oscillators outperforms existing state-of-the-art methods on benchmark problems across various metrics. Consequently, the proposed method improves the generalization capabilities of PIML, providing accurate solutions for extrapolation and prediction beyond the training data.

Physics-informed neural networks for solving forward and inverse problems in complex beam systems

This paper proposes a new framework using physics-informed neural networks (PINNs) to simulate complex structural systems that consist of single and double beams based on Euler-Bernoulli and Timoshenko theory, where the double beams are connected with a Winkler foundation. In particular, forward and inverse problems for the Euler-Bernoulli and Timoshenko partial differential equations (PDEs) are solved using nondimensional equations with the physics-informed loss function. Higher-order complex beam PDEs are efficiently solved for forward problems to compute the transverse displacements and cross-sectional rotations with less than 1e-3 percent error. Furthermore, inverse problems are robustly solved to determine the unknown dimensionless model parameters and applied force in the entire space-time domain, even in the case of noisy data. The results suggest that PINNs are a promising strategy for solving problems in engineering structures and machines involving beam systems.