Transfer learning for improved generalizability in causal physics-informed neural networks for beam simulations
Paper and Code
Nov 01, 2023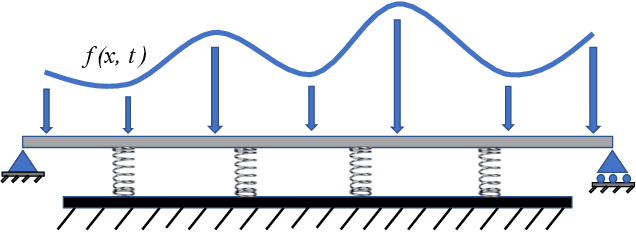

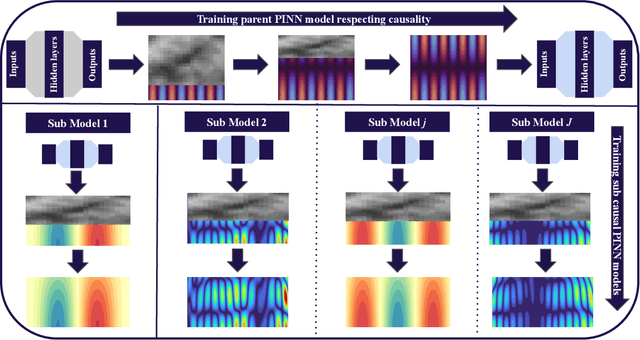

This paper introduces a novel methodology for simulating the dynamics of beams on elastic foundations. Specifically, Euler-Bernoulli and Timoshenko beam models on the Winkler foundation are simulated using a transfer learning approach within a causality-respecting physics-informed neural network (PINN) framework. Conventional PINNs encounter challenges in handling large space-time domains, even for problems with closed-form analytical solutions. A causality-respecting PINN loss function is employed to overcome this limitation, effectively capturing the underlying physics. However, it is observed that the causality-respecting PINN lacks generalizability. We propose using solutions to similar problems instead of training from scratch by employing transfer learning while adhering to causality to accelerate convergence and ensure accurate results across diverse scenarios. Numerical experiments on the Euler-Bernoulli beam highlight the efficacy of the proposed approach for various initial conditions, including those with noise in the initial data. Furthermore, the potential of the proposed method is demonstrated for the Timoshenko beam in an extended spatial and temporal domain. Several comparisons suggest that the proposed method accurately captures the inherent dynamics, outperforming the state-of-the-art physics-informed methods under standard $L^2$-norm metric and accelerating convergence.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge