GeoFUSE: A High-Efficiency Surrogate Model for Seawater Intrusion Prediction and Uncertainty Reduction

Seawater intrusion into coastal aquifers poses a significant threat to groundwater resources, especially with rising sea levels due to climate change. Accurate modeling and uncertainty quantification of this process are crucial but are often hindered by the high computational costs of traditional numerical simulations. In this work, we develop GeoFUSE, a novel deep-learning-based surrogate framework that integrates the U-Net Fourier Neural Operator (U-FNO) with Principal Component Analysis (PCA) and Ensemble Smoother with Multiple Data Assimilation (ESMDA). GeoFUSE enables fast and efficient simulation of seawater intrusion while significantly reducing uncertainty in model predictions. We apply GeoFUSE to a 2D cross-section of the Beaver Creek tidal stream-floodplain system in Washington State. Using 1,500 geological realizations, we train the U-FNO surrogate model to approximate salinity distribution and accumulation. The U-FNO model successfully reduces the computational time from hours (using PFLOTRAN simulations) to seconds, achieving a speedup of approximately 360,000 times while maintaining high accuracy. By integrating measurement data from monitoring wells, the framework significantly reduces geological uncertainty and improves the predictive accuracy of the salinity distribution over a 20-year period. Our results demonstrate that GeoFUSE improves computational efficiency and provides a robust tool for real-time uncertainty quantification and decision making in groundwater management. Future work will extend GeoFUSE to 3D models and incorporate additional factors such as sea-level rise and extreme weather events, making it applicable to a broader range of coastal and subsurface flow systems.

Baseflow identification via explainable AI with Kolmogorov-Arnold networks

Hydrological models often involve constitutive laws that may not be optimal in every application. We propose to replace such laws with the Kolmogorov-Arnold networks (KANs), a class of neural networks designed to identify symbolic expressions. We demonstrate KAN's potential on the problem of baseflow identification, a notoriously challenging task plagued by significant uncertainty. KAN-derived functional dependencies of the baseflow components on the aridity index outperform their original counterparts. On a test set, they increase the Nash-Sutcliffe Efficiency (NSE) by 67%, decrease the root mean squared error by 30%, and increase the Kling-Gupta efficiency by 24%. This superior performance is achieved while reducing the number of fitting parameters from three to two. Next, we use data from 378 catchments across the continental United States to refine the water-balance equation at the mean-annual scale. The KAN-derived equations based on the refined water balance outperform both the current aridity index model, with up to a 105% increase in NSE, and the KAN-derived equations based on the original water balance. While the performance of our model and tree-based machine learning methods is similar, KANs offer the advantage of simplicity and transparency and require no specific software or computational tools. This case study focuses on the aridity index formulation, but the approach is flexible and transferable to other hydrological processes.

Differentiable modeling to unify machine learning and physical models and advance Geosciences

Process-Based Modeling (PBM) and Machine Learning (ML) are often perceived as distinct paradigms in the geosciences. Here we present differentiable geoscientific modeling as a powerful pathway toward dissolving the perceived barrier between them and ushering in a paradigm shift. For decades, PBM offered benefits in interpretability and physical consistency but struggled to efficiently leverage large datasets. ML methods, especially deep networks, presented strong predictive skills yet lacked the ability to answer specific scientific questions. While various methods have been proposed for ML-physics integration, an important underlying theme -- differentiable modeling -- is not sufficiently recognized. Here we outline the concepts, applicability, and significance of differentiable geoscientific modeling (DG). "Differentiable" refers to accurately and efficiently calculating gradients with respect to model variables, critically enabling the learning of high-dimensional unknown relationships. DG refers to a range of methods connecting varying amounts of prior knowledge to neural networks and training them together, capturing a different scope than physics-guided machine learning and emphasizing first principles. Preliminary evidence suggests DG offers better interpretability and causality than ML, improved generalizability and extrapolation capability, and strong potential for knowledge discovery, while approaching the performance of purely data-driven ML. DG models require less training data while scaling favorably in performance and efficiency with increasing amounts of data. With DG, geoscientists may be better able to frame and investigate questions, test hypotheses, and discover unrecognized linkages.

Learning from learning machines: a new generation of AI technology to meet the needs of science

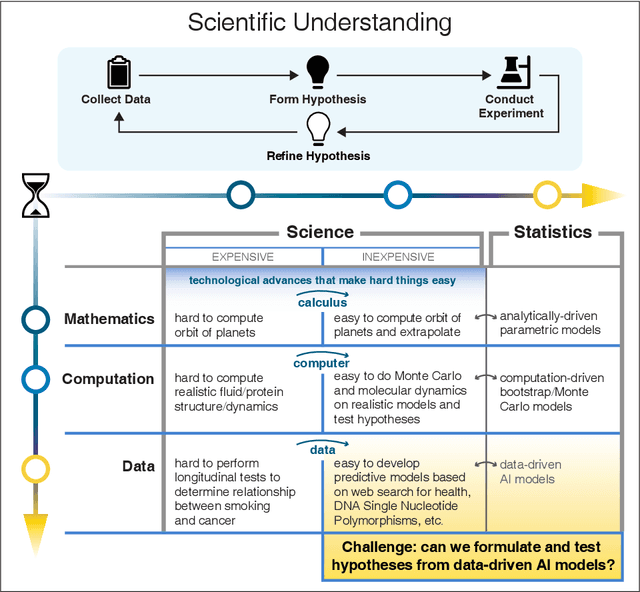
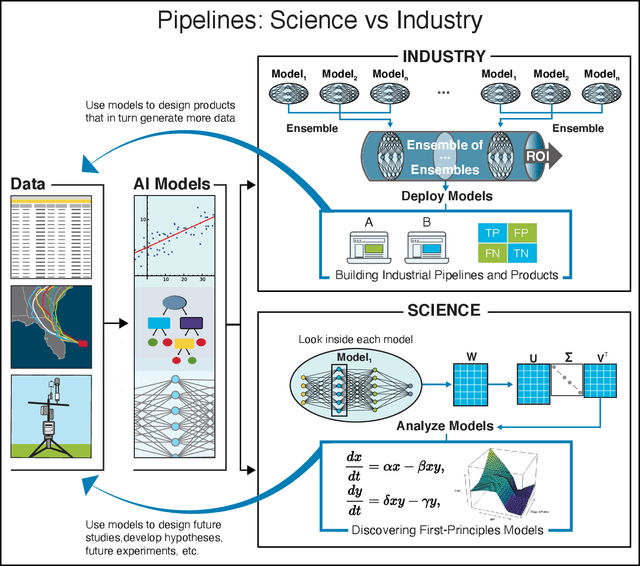
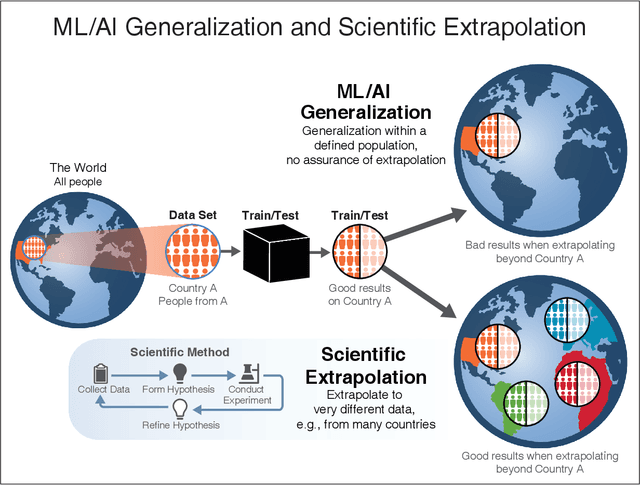
We outline emerging opportunities and challenges to enhance the utility of AI for scientific discovery. The distinct goals of AI for industry versus the goals of AI for science create tension between identifying patterns in data versus discovering patterns in the world from data. If we address the fundamental challenges associated with "bridging the gap" between domain-driven scientific models and data-driven AI learning machines, then we expect that these AI models can transform hypothesis generation, scientific discovery, and the scientific process itself.