Methodology for Interpretable Reinforcement Learning for Optimizing Mechanical Ventilation

Mechanical ventilation is a critical life-support intervention that uses a machine to deliver controlled air and oxygen to a patient's lungs, assisting or replacing spontaneous breathing. While several data-driven approaches have been proposed to optimize ventilator control strategies, they often lack interpretability and agreement with general domain knowledge. This paper proposes a methodology for interpretable reinforcement learning (RL) using decision trees for mechanical ventilation control. Using a causal, nonparametric model-based off-policy evaluation, we evaluate the policies in their ability to gain increases in SpO2 while avoiding aggressive ventilator settings which are known to cause ventilator induced lung injuries and other complications. Numerical experiments using MIMIC-III data on the stays of real patients' intensive care unit stays demonstrate that the decision tree policy outperforms the behavior cloning policy and is comparable to state-of-the-art RL policy. Future work concerns better aligning the cost function with medical objectives to generate deeper clinical insights.

Tensor Completion via Integer Optimization

The main challenge with the tensor completion problem is a fundamental tension between computation power and the information-theoretic sample complexity rate. Past approaches either achieve the information-theoretic rate but lack practical algorithms to compute the corresponding solution, or have polynomial-time algorithms that require an exponentially-larger number of samples for low estimation error. This paper develops a novel tensor completion algorithm that resolves this tension by achieving both provable convergence (in numerical tolerance) in a linear number of oracle steps and the information-theoretic rate. Our approach formulates tensor completion as a convex optimization problem constrained using a gauge-based tensor norm, which is defined in a way that allows the use of integer linear optimization to solve linear separation problems over the unit-ball in this new norm. Adaptations based on this insight are incorporated into a Frank-Wolfe variant to build our algorithm. We show our algorithm scales-well using numerical experiments on tensors with up to ten million entries.

Estimating and Incentivizing Imperfect-Knowledge Agents with Hidden Rewards

In practice, incentive providers (i.e., principals) often cannot observe the reward realizations of incentivized agents, which is in contrast to many principal-agent models that have been previously studied. This information asymmetry challenges the principal to consistently estimate the agent's unknown rewards by solely watching the agent's decisions, which becomes even more challenging when the agent has to learn its own rewards. This complex setting is observed in various real-life scenarios ranging from renewable energy storage contracts to personalized healthcare incentives. Hence, it offers not only interesting theoretical questions but also wide practical relevance. This paper explores a repeated adverse selection game between a self-interested learning agent and a learning principal. The agent tackles a multi-armed bandit (MAB) problem to maximize their expected reward plus incentive. On top of the agent's learning, the principal trains a parallel algorithm and faces a trade-off between consistently estimating the agent's unknown rewards and maximizing their own utility by offering adaptive incentives to lead the agent. For a non-parametric model, we introduce an estimator whose only input is the history of principal's incentives and agent's choices. We unite this estimator with a proposed data-driven incentive policy within a MAB framework. Without restricting the type of the agent's algorithm, we prove finite-sample consistency of the estimator and a rigorous regret bound for the principal by considering the sequential externality imposed by the agent. Lastly, our theoretical results are reinforced by simulations justifying applicability of our framework to green energy aggregator contracts.

Repeated Principal-Agent Games with Unobserved Agent Rewards and Perfect-Knowledge Agents

Motivated by a number of real-world applications from domains like healthcare and sustainable transportation, in this paper we study a scenario of repeated principal-agent games within a multi-armed bandit (MAB) framework, where: the principal gives a different incentive for each bandit arm, the agent picks a bandit arm to maximize its own expected reward plus incentive, and the principal observes which arm is chosen and receives a reward (different than that of the agent) for the chosen arm. Designing policies for the principal is challenging because the principal cannot directly observe the reward that the agent receives for their chosen actions, and so the principal cannot directly learn the expected reward using existing estimation techniques. As a result, the problem of designing policies for this scenario, as well as similar ones, remains mostly unexplored. In this paper, we construct a policy that achieves a low regret (i.e., square-root regret up to a log factor) in this scenario for the case where the agent has perfect-knowledge about its own expected rewards for each bandit arm. We design our policy by first constructing an estimator for the agent's expected reward for each bandit arm. Since our estimator uses as data the sequence of incentives offered and subsequently chosen arms, the principal's estimation can be regarded as an analogy of online inverse optimization in MAB's. Next we construct a policy that we prove achieves a low regret by deriving finite-sample concentration bounds for our estimator. We conclude with numerical simulations demonstrating the applicability of our policy to real-life setting from collaborative transportation planning.

Accelerated Nonnegative Tensor Completion via Integer Programming

The problem of tensor completion has applications in healthcare, computer vision, and other domains. However, past approaches to tensor completion have faced a tension in that they either have polynomial-time computation but require exponentially more samples than the information-theoretic rate, or they use fewer samples but require solving NP-hard problems for which there are no known practical algorithms. A recent approach, based on integer programming, resolves this tension for nonnegative tensor completion. It achieves the information-theoretic sample complexity rate and deploys the Blended Conditional Gradients algorithm, which requires a linear (in numerical tolerance) number of oracle steps to converge to the global optimum. The tradeoff in this approach is that, in the worst case, the oracle step requires solving an integer linear program. Despite this theoretical limitation, numerical experiments show that this algorithm can, on certain instances, scale up to 100 million entries while running on a personal computer. The goal of this paper is to further enhance this algorithm, with the intention to expand both the breadth and scale of instances that can be solved. We explore several variants that can maintain the same theoretical guarantees as the algorithm, but offer potentially faster computation. We consider different data structures, acceleration of gradient descent steps, and the use of the Blended Pairwise Conditional Gradients algorithm. We describe the original approach and these variants, and conduct numerical experiments in order to explore various tradeoffs in these algorithmic design choices.

Learning from learning machines: a new generation of AI technology to meet the needs of science

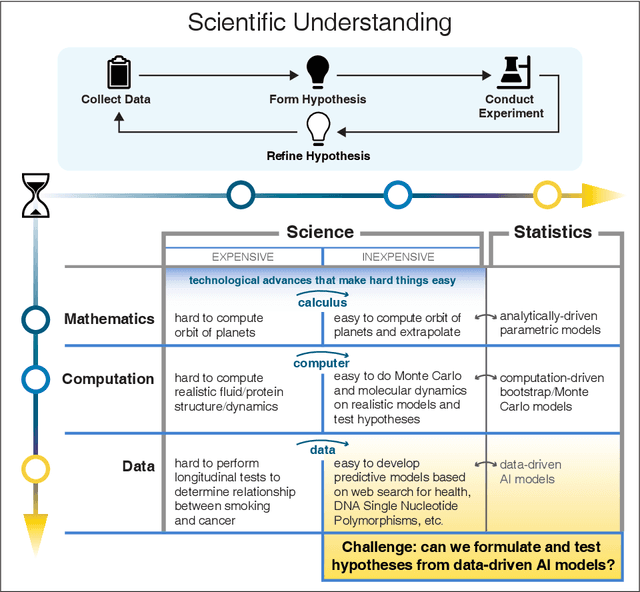
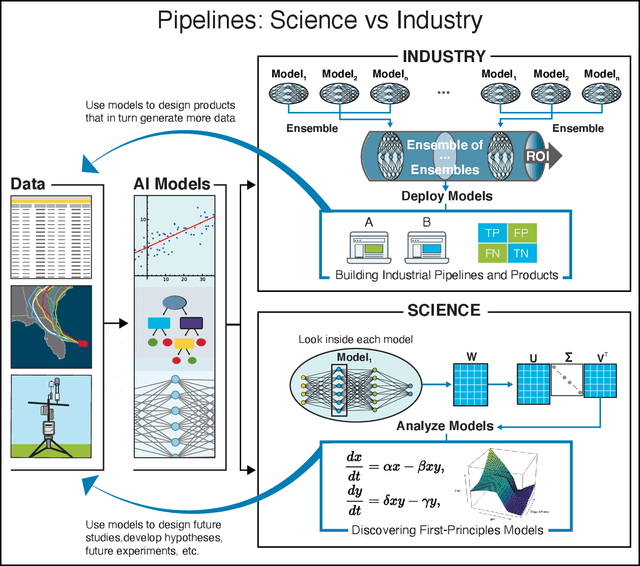
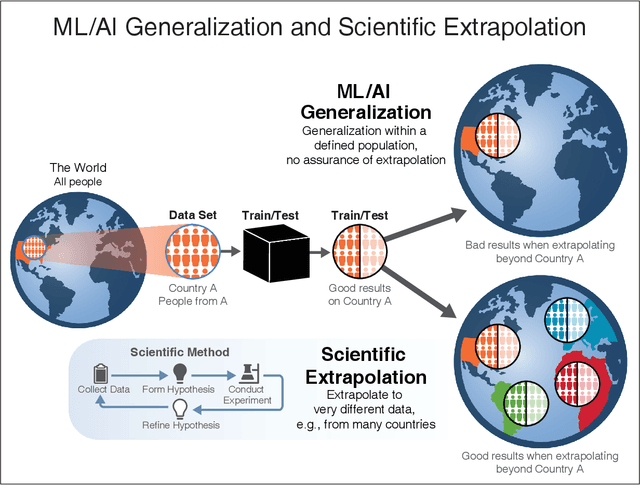
We outline emerging opportunities and challenges to enhance the utility of AI for scientific discovery. The distinct goals of AI for industry versus the goals of AI for science create tension between identifying patterns in data versus discovering patterns in the world from data. If we address the fundamental challenges associated with "bridging the gap" between domain-driven scientific models and data-driven AI learning machines, then we expect that these AI models can transform hypothesis generation, scientific discovery, and the scientific process itself.

Nonnegative Tensor Completion via Integer Optimization

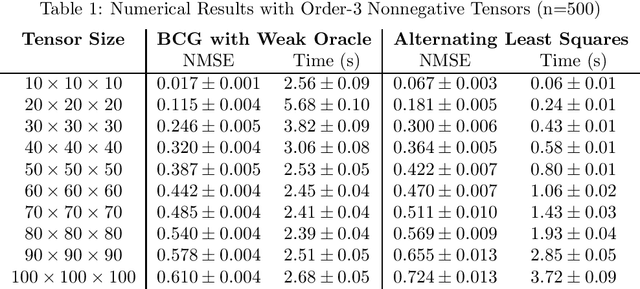
Unlike matrix completion, no algorithm for the tensor completion problem has so far been shown to achieve the information-theoretic sample complexity rate. This paper develops a new algorithm for the special case of completion for nonnegative tensors. We prove that our algorithm converges in a linear (in numerical tolerance) number of oracle steps, while achieving the information-theoretic rate. Our approach is to define a new norm for nonnegative tensors using the gauge of a specific 0-1 polytope that we construct. Because the norm is defined using a 0-1 polytope, this means we can use integer linear programming to solve linear separation problems over the polytope. We combine this insight with a variant of the Frank-Wolfe algorithm to construct our numerical algorithm, and we demonstrate its effectiveness and scalability through experiments.

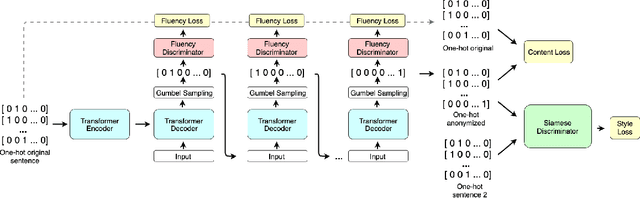
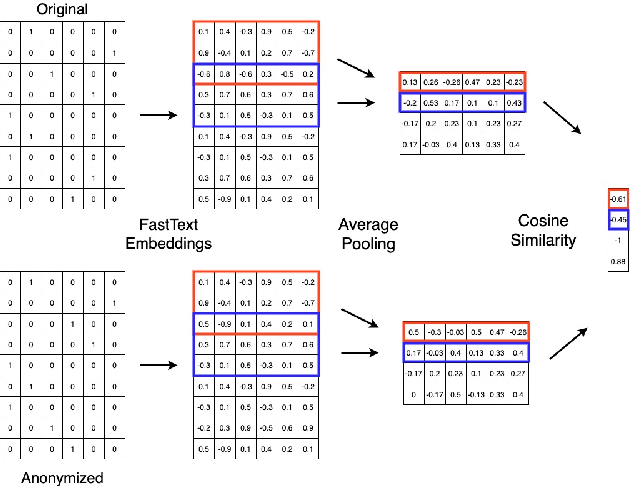
Protecting Anonymous Speech: A Generative Adversarial Network Methodology for Removing Stylistic Indicators in Text

With Internet users constantly leaving a trail of text, whether through blogs, emails, or social media posts, the ability to write and protest anonymously is being eroded because artificial intelligence, when given a sample of previous work, can match text with its author out of hundreds of possible candidates. Existing approaches to authorship anonymization, also known as authorship obfuscation, often focus on protecting binary demographic attributes rather than identity as a whole. Even those that do focus on obfuscating identity require manual feedback, lose the coherence of the original sentence, or only perform well given a limited subset of authors. In this paper, we develop a new approach to authorship anonymization by constructing a generative adversarial network that protects identity and optimizes for three different losses corresponding to anonymity, fluency, and content preservation. Our fully automatic method achieves comparable results to other methods in terms of content preservation and fluency, but greatly outperforms baselines in regards to anonymization. Moreover, our approach is able to generalize well to an open-set context and anonymize sentences from authors it has not encountered before.

Regret Analysis of Learning-Based MPC with Partially-Unknown Cost Function

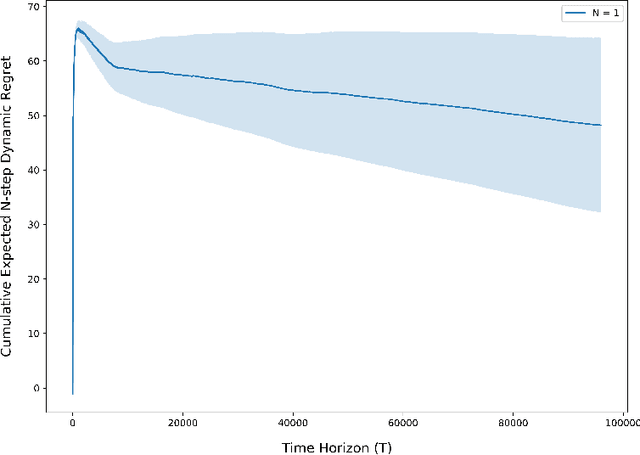
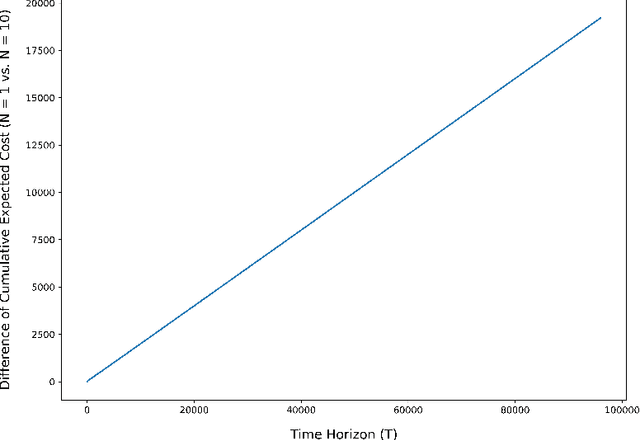
The exploration/exploitation trade-off is an inherent challenge in data-driven and adaptive control. Though this trade-off has been studied for multi-armed bandits, reinforcement learning (RL) for finite Markov chains, and RL for linear control systems; it is less well-studied for learning-based control of nonlinear control systems. A significant theoretical challenge in the nonlinear setting is that, unlike the linear case, there is no explicit characterization of an optimal controller for a given set of cost and system parameters. We propose in this paper the use of a finite-horizon oracle controller with perfect knowledge of all system parameters as a reference for optimal control actions. First, this allows us to propose a new regret notion with respect to this oracle finite-horizon controller. Second, this allows us to develop learning-based policies that we prove achieve low regret (i.e., square-root regret up to a log-squared factor) with respect to this oracle finite-horizon controller. This policy is developed in the context of learning-based model predictive control (LBMPC). We conduct a statistical analysis to prove finite sample concentration bounds for the estimation step of our policy, and then we perform a control-theoretic analysis using techniques from MPC- and optimization-theory to show this policy ensures closed-loop stability and achieves low regret. We conclude with numerical experiments on a model of heating, ventilation, and air-conditioning (HVAC) systems that show the low regret of our policy in a setting where the cost function is partially-unknown to the controller.

Covariance-Robust Dynamic Watermarking

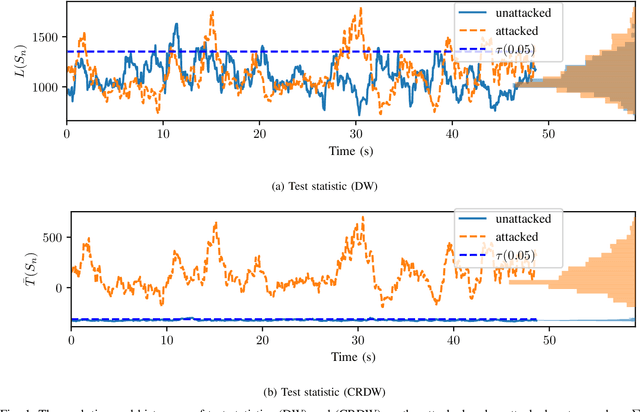
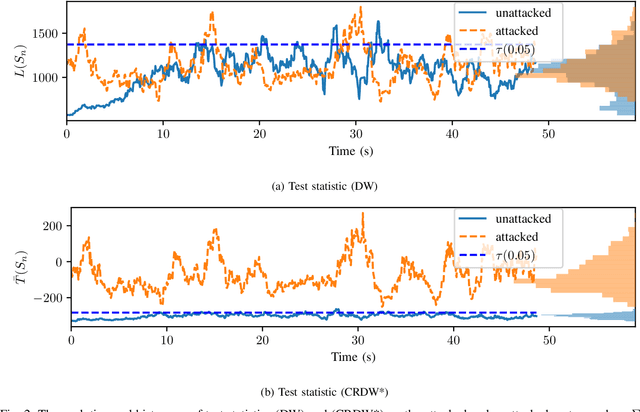
Attack detection and mitigation strategies for cyberphysical systems (CPS) are an active area of research, and researchers have developed a variety of attack-detection tools such as dynamic watermarking. However, such methods often make assumptions that are difficult to guarantee, such as exact knowledge of the distribution of measurement noise. Here, we develop a new dynamic watermarking method that we call covariance-robust dynamic watermarking, which is able to handle uncertainties in the covariance of measurement noise. Specifically, we consider two cases. In the first this covariance is fixed but unknown, and in the second this covariance is slowly-varying. For our tests, we only require knowledge of a set within which the covariance lies. Furthermore, we connect this problem to that of algorithmic fairness and the nascent field of fair hypothesis testing, and we show that our tests satisfy some notions of fairness. Finally, we exhibit the efficacy of our tests on empirical examples chosen to reflect values observed in a standard simulation model of autonomous vehicles.