Nonnegative Tensor Completion via Integer Optimization
Paper and Code
Nov 08, 2021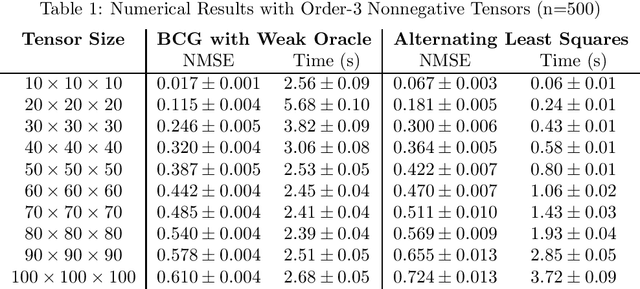

Unlike matrix completion, no algorithm for the tensor completion problem has so far been shown to achieve the information-theoretic sample complexity rate. This paper develops a new algorithm for the special case of completion for nonnegative tensors. We prove that our algorithm converges in a linear (in numerical tolerance) number of oracle steps, while achieving the information-theoretic rate. Our approach is to define a new norm for nonnegative tensors using the gauge of a specific 0-1 polytope that we construct. Because the norm is defined using a 0-1 polytope, this means we can use integer linear programming to solve linear separation problems over the polytope. We combine this insight with a variant of the Frank-Wolfe algorithm to construct our numerical algorithm, and we demonstrate its effectiveness and scalability through experiments.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge