Estimating and Incentivizing Imperfect-Knowledge Agents with Hidden Rewards

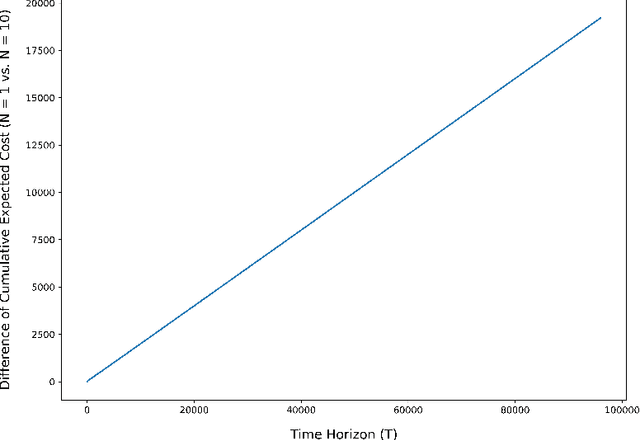
In practice, incentive providers (i.e., principals) often cannot observe the reward realizations of incentivized agents, which is in contrast to many principal-agent models that have been previously studied. This information asymmetry challenges the principal to consistently estimate the agent's unknown rewards by solely watching the agent's decisions, which becomes even more challenging when the agent has to learn its own rewards. This complex setting is observed in various real-life scenarios ranging from renewable energy storage contracts to personalized healthcare incentives. Hence, it offers not only interesting theoretical questions but also wide practical relevance. This paper explores a repeated adverse selection game between a self-interested learning agent and a learning principal. The agent tackles a multi-armed bandit (MAB) problem to maximize their expected reward plus incentive. On top of the agent's learning, the principal trains a parallel algorithm and faces a trade-off between consistently estimating the agent's unknown rewards and maximizing their own utility by offering adaptive incentives to lead the agent. For a non-parametric model, we introduce an estimator whose only input is the history of principal's incentives and agent's choices. We unite this estimator with a proposed data-driven incentive policy within a MAB framework. Without restricting the type of the agent's algorithm, we prove finite-sample consistency of the estimator and a rigorous regret bound for the principal by considering the sequential externality imposed by the agent. Lastly, our theoretical results are reinforced by simulations justifying applicability of our framework to green energy aggregator contracts.

Repeated Principal-Agent Games with Unobserved Agent Rewards and Perfect-Knowledge Agents

Motivated by a number of real-world applications from domains like healthcare and sustainable transportation, in this paper we study a scenario of repeated principal-agent games within a multi-armed bandit (MAB) framework, where: the principal gives a different incentive for each bandit arm, the agent picks a bandit arm to maximize its own expected reward plus incentive, and the principal observes which arm is chosen and receives a reward (different than that of the agent) for the chosen arm. Designing policies for the principal is challenging because the principal cannot directly observe the reward that the agent receives for their chosen actions, and so the principal cannot directly learn the expected reward using existing estimation techniques. As a result, the problem of designing policies for this scenario, as well as similar ones, remains mostly unexplored. In this paper, we construct a policy that achieves a low regret (i.e., square-root regret up to a log factor) in this scenario for the case where the agent has perfect-knowledge about its own expected rewards for each bandit arm. We design our policy by first constructing an estimator for the agent's expected reward for each bandit arm. Since our estimator uses as data the sequence of incentives offered and subsequently chosen arms, the principal's estimation can be regarded as an analogy of online inverse optimization in MAB's. Next we construct a policy that we prove achieves a low regret by deriving finite-sample concentration bounds for our estimator. We conclude with numerical simulations demonstrating the applicability of our policy to real-life setting from collaborative transportation planning.

Regret Analysis of Learning-Based MPC with Partially-Unknown Cost Function

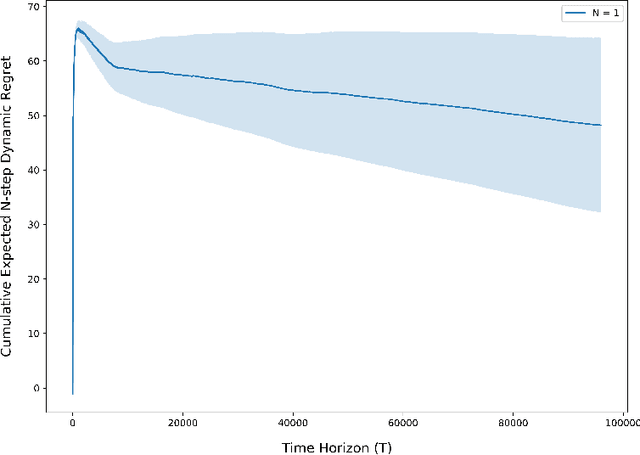
The exploration/exploitation trade-off is an inherent challenge in data-driven and adaptive control. Though this trade-off has been studied for multi-armed bandits, reinforcement learning (RL) for finite Markov chains, and RL for linear control systems; it is less well-studied for learning-based control of nonlinear control systems. A significant theoretical challenge in the nonlinear setting is that, unlike the linear case, there is no explicit characterization of an optimal controller for a given set of cost and system parameters. We propose in this paper the use of a finite-horizon oracle controller with perfect knowledge of all system parameters as a reference for optimal control actions. First, this allows us to propose a new regret notion with respect to this oracle finite-horizon controller. Second, this allows us to develop learning-based policies that we prove achieve low regret (i.e., square-root regret up to a log-squared factor) with respect to this oracle finite-horizon controller. This policy is developed in the context of learning-based model predictive control (LBMPC). We conduct a statistical analysis to prove finite sample concentration bounds for the estimation step of our policy, and then we perform a control-theoretic analysis using techniques from MPC- and optimization-theory to show this policy ensures closed-loop stability and achieves low regret. We conclude with numerical experiments on a model of heating, ventilation, and air-conditioning (HVAC) systems that show the low regret of our policy in a setting where the cost function is partially-unknown to the controller.