Fast and Efficient MMD-based Fair PCA via Optimization over Stiefel Manifold

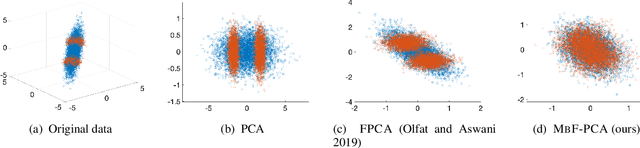
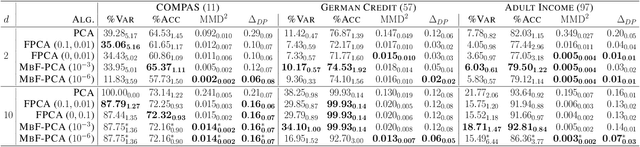
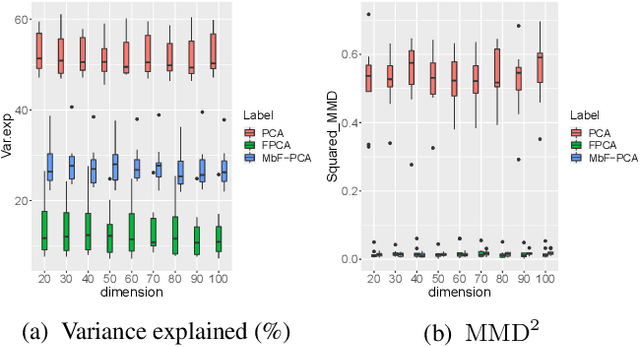
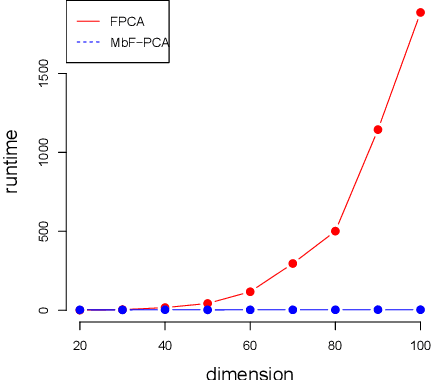
This paper defines fair principal component analysis (PCA) as minimizing the maximum mean discrepancy (MMD) between dimensionality-reduced conditional distributions of different protected classes. The incorporation of MMD naturally leads to an exact and tractable mathematical formulation of fairness with good statistical properties. We formulate the problem of fair PCA subject to MMD constraints as a non-convex optimization over the Stiefel manifold and solve it using the Riemannian Exact Penalty Method with Smoothing (REPMS; Liu and Boumal, 2019). Importantly, we provide local optimality guarantees and explicitly show the theoretical effect of each hyperparameter in practical settings, extending previous results. Experimental comparisons based on synthetic and UCI datasets show that our approach outperforms prior work in explained variance, fairness, and runtime.

Covariance-Robust Dynamic Watermarking

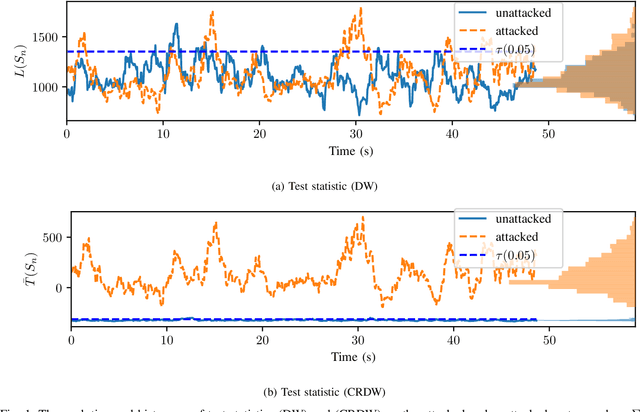
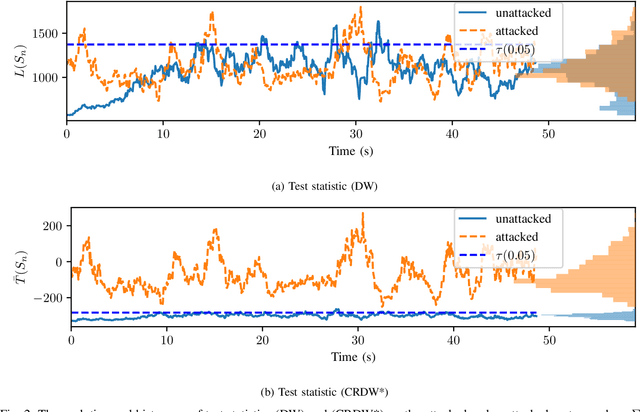
Attack detection and mitigation strategies for cyberphysical systems (CPS) are an active area of research, and researchers have developed a variety of attack-detection tools such as dynamic watermarking. However, such methods often make assumptions that are difficult to guarantee, such as exact knowledge of the distribution of measurement noise. Here, we develop a new dynamic watermarking method that we call covariance-robust dynamic watermarking, which is able to handle uncertainties in the covariance of measurement noise. Specifically, we consider two cases. In the first this covariance is fixed but unknown, and in the second this covariance is slowly-varying. For our tests, we only require knowledge of a set within which the covariance lies. Furthermore, we connect this problem to that of algorithmic fairness and the nascent field of fair hypothesis testing, and we show that our tests satisfy some notions of fairness. Finally, we exhibit the efficacy of our tests on empirical examples chosen to reflect values observed in a standard simulation model of autonomous vehicles.

Convex Formulations for Fair Principal Component Analysis

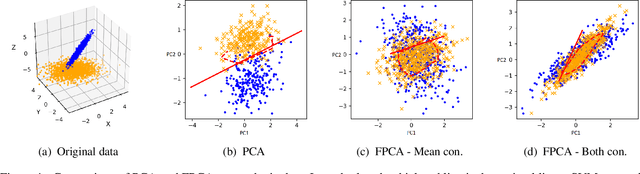
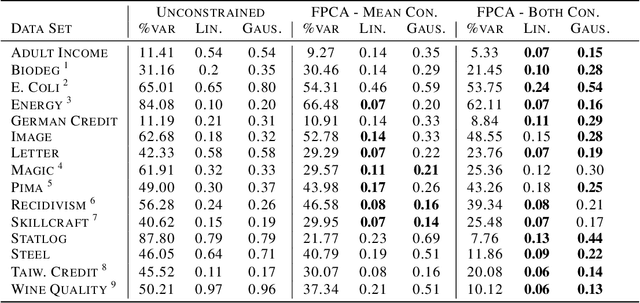
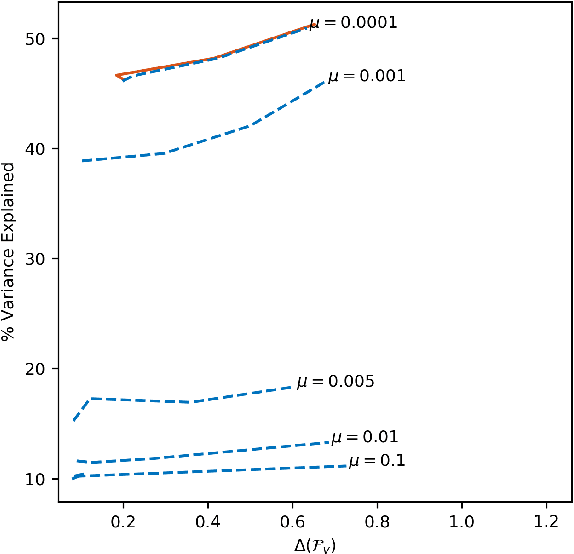
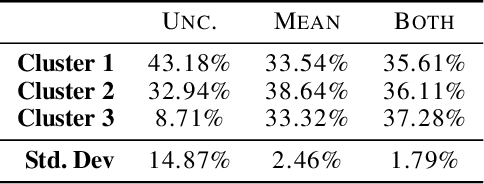
Though there is a growing body of literature on fairness for supervised learning, the problem of incorporating fairness into unsupervised learning has been less well-studied. This paper studies fairness in the context of principal component analysis (PCA). We first present a definition of fairness for dimensionality reduction, and our definition can be interpreted as saying that a reduction is fair if information about a protected class (e.g., race or gender) cannot be inferred from the dimensionality-reduced data points. Next, we develop convex optimization formulations that can improve the fairness (with respect to our definition) of PCA and kernel PCA. These formulations are semidefinite programs (SDP's), and we demonstrate the effectiveness of our formulations using several datasets. We conclude by showing how our approach can be used to perform a fair (with respect to age) clustering of health data that may be used to set health insurance rates.

Average Margin Regularization for Classifiers

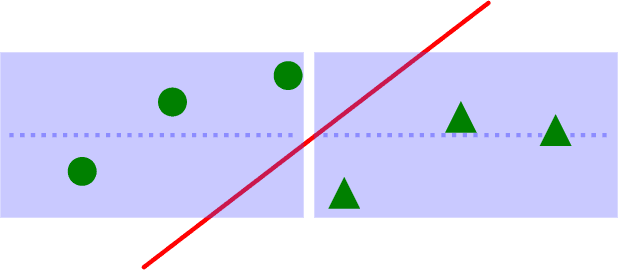
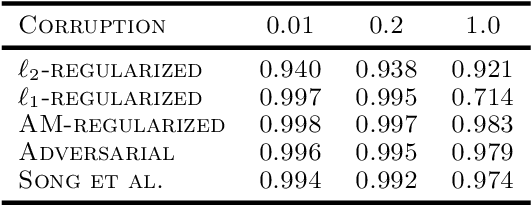
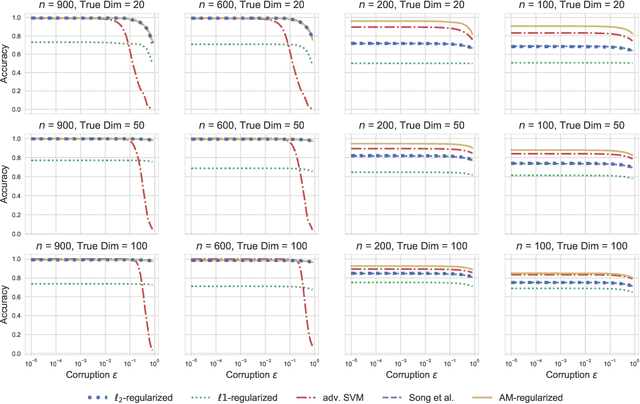
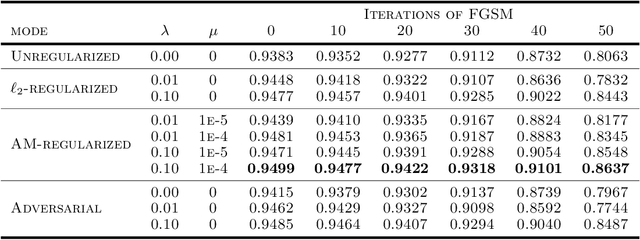
Adversarial robustness has become an important research topic given empirical demonstrations on the lack of robustness of deep neural networks. Unfortunately, recent theoretical results suggest that adversarial training induces a strict tradeoff between classification accuracy and adversarial robustness. In this paper, we propose and then study a new regularization for any margin classifier or deep neural network. We motivate this regularization by a novel generalization bound that shows a tradeoff in classifier accuracy between maximizing its margin and average margin. We thus call our approach an average margin (AM) regularization, and it consists of a linear term added to the objective. We theoretically show that for certain distributions AM regularization can both improve classifier accuracy and robustness to adversarial attacks. We conclude by using both synthetic and real data to empirically show that AM regularization can strictly improve both accuracy and robustness for support vector machine's (SVM's) and deep neural networks, relative to unregularized classifiers and adversarially trained classifiers.

Spectral Algorithms for Computing Fair Support Vector Machines

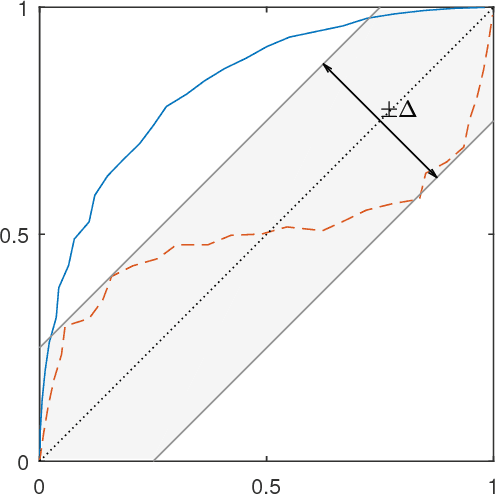
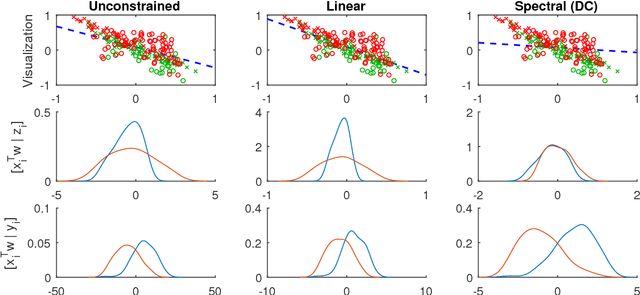
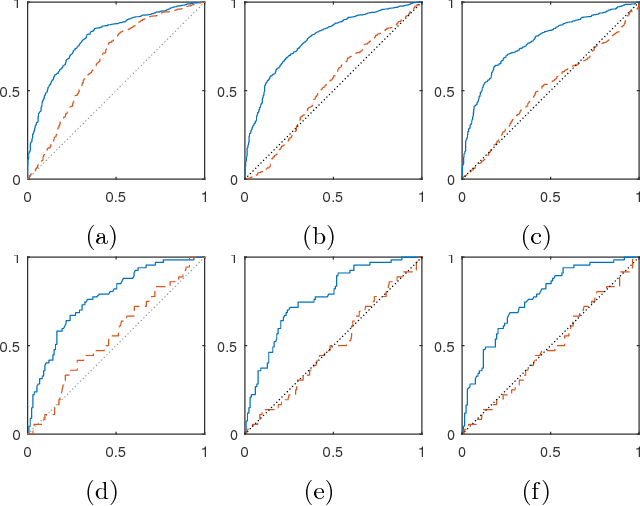
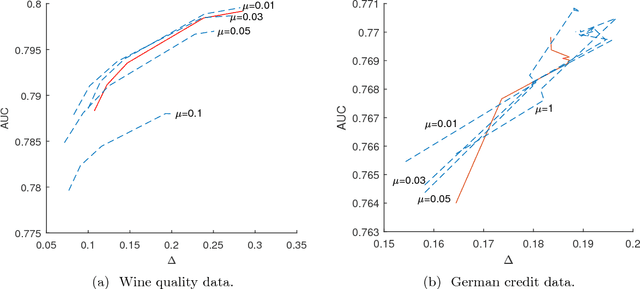
Classifiers and rating scores are prone to implicitly codifying biases, which may be present in the training data, against protected classes (i.e., age, gender, or race). So it is important to understand how to design classifiers and scores that prevent discrimination in predictions. This paper develops computationally tractable algorithms for designing accurate but fair support vector machines (SVM's). Our approach imposes a constraint on the covariance matrices conditioned on each protected class, which leads to a nonconvex quadratic constraint in the SVM formulation. We develop iterative algorithms to compute fair linear and kernel SVM's, which solve a sequence of relaxations constructed using a spectral decomposition of the nonconvex constraint. Its effectiveness in achieving high prediction accuracy while ensuring fairness is shown through numerical experiments on several data sets.