Spectral Algorithms for Computing Fair Support Vector Machines
Paper and Code
Oct 16, 2017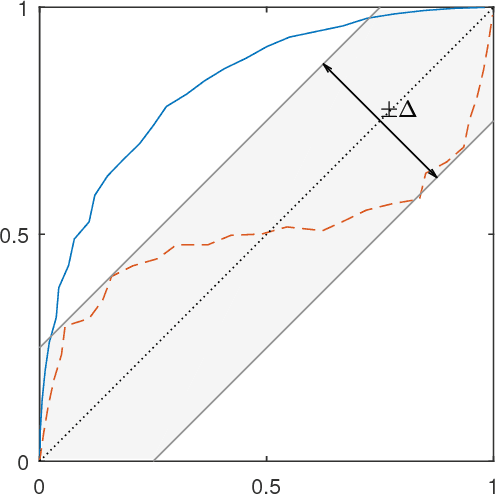
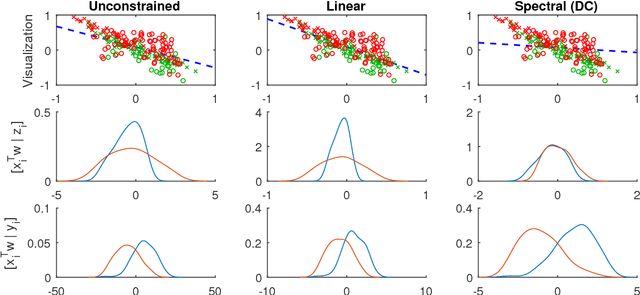
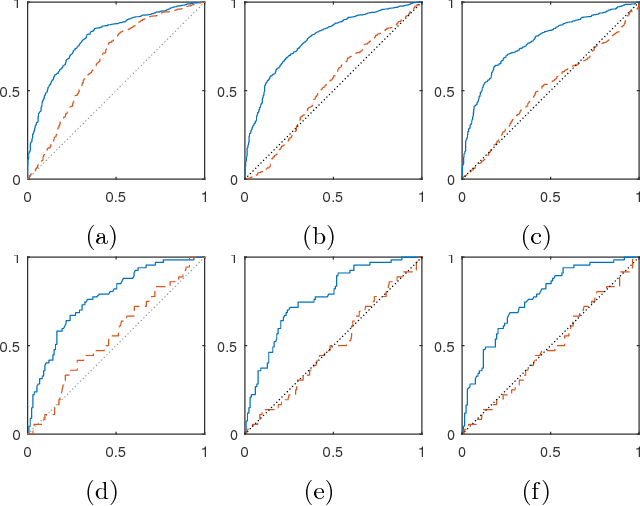
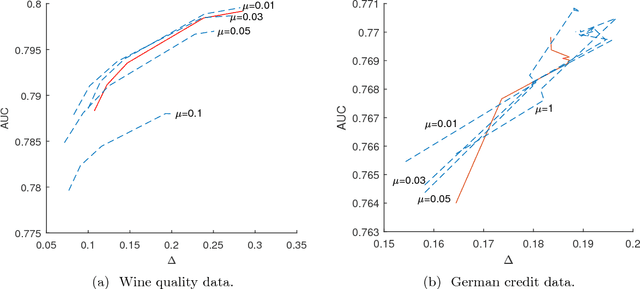
Classifiers and rating scores are prone to implicitly codifying biases, which may be present in the training data, against protected classes (i.e., age, gender, or race). So it is important to understand how to design classifiers and scores that prevent discrimination in predictions. This paper develops computationally tractable algorithms for designing accurate but fair support vector machines (SVM's). Our approach imposes a constraint on the covariance matrices conditioned on each protected class, which leads to a nonconvex quadratic constraint in the SVM formulation. We develop iterative algorithms to compute fair linear and kernel SVM's, which solve a sequence of relaxations constructed using a spectral decomposition of the nonconvex constraint. Its effectiveness in achieving high prediction accuracy while ensuring fairness is shown through numerical experiments on several data sets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge