Interaction Decompositions for Tensor Network Regression

It is well known that tensor network regression models operate on an exponentially large feature space, but questions remain as to how effectively they are able to utilize this space. Using the polynomial featurization from Novikov et al., we propose the interaction decomposition as a tool that can assess the relative importance of different regressors as a function of their polynomial degree. We apply this decomposition to tensor ring and tree tensor network models trained on the MNIST and Fashion MNIST datasets, and find that up to 75% of interaction degrees are contributing meaningfully to these models. We also introduce a new type of tensor network model that is explicitly trained on only a small subset of interaction degrees, and find that these models are able to match or even outperform the full models using only a fraction of the exponential feature space. This suggests that standard tensor network models utilize their polynomial regressors in an inefficient manner, with the lower degree terms being vastly under-utilized.

Towards Quantum Machine Learning with Tensor Networks

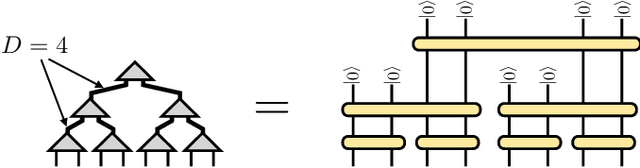
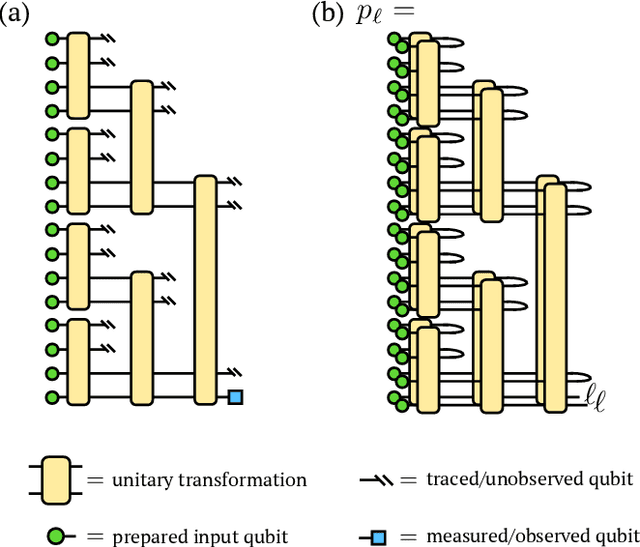
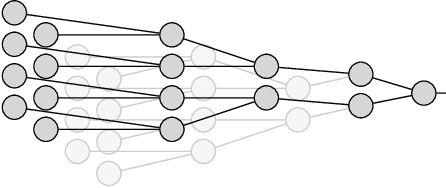
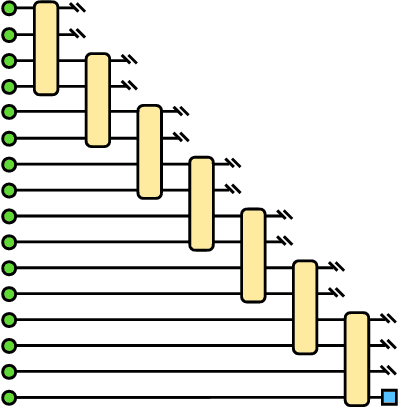
Machine learning is a promising application of quantum computing, but challenges remain as near-term devices will have a limited number of physical qubits and high error rates. Motivated by the usefulness of tensor networks for machine learning in the classical context, we propose quantum computing approaches to both discriminative and generative learning, with circuits based on tree and matrix product state tensor networks that could have benefits for near-term devices. The result is a unified framework where classical and quantum computing can benefit from the same theoretical and algorithmic developments, and the same model can be trained classically then transferred to the quantum setting for additional optimization. Tensor network circuits can also provide qubit-efficient schemes where, depending on the architecture, the number of physical qubits required scales only logarithmically with, or independently of the input or output data sizes. We demonstrate our proposals with numerical experiments, training a discriminative model to perform handwriting recognition using a optimization procedure that could be carried out on quantum hardware, and testing the noise resilience of the trained model.