Quantum Tensor Networks, Stochastic Processes, and Weighted Automata

Modeling joint probability distributions over sequences has been studied from many perspectives. The physics community developed matrix product states, a tensor-train decomposition for probabilistic modeling, motivated by the need to tractably model many-body systems. But similar models have also been studied in the stochastic processes and weighted automata literature, with little work on how these bodies of work relate to each other. We address this gap by showing how stationary or uniform versions of popular quantum tensor network models have equivalent representations in the stochastic processes and weighted automata literature, in the limit of infinitely long sequences. We demonstrate several equivalence results between models used in these three communities: (i) uniform variants of matrix product states, Born machines and locally purified states from the quantum tensor networks literature, (ii) predictive state representations, hidden Markov models, norm-observable operator models and hidden quantum Markov models from the stochastic process literature,and (iii) stochastic weighted automata, probabilistic automata and quadratic automata from the formal languages literature. Such connections may open the door for results and methods developed in one area to be applied in another.

Expressiveness and Learning of Hidden Quantum Markov Models

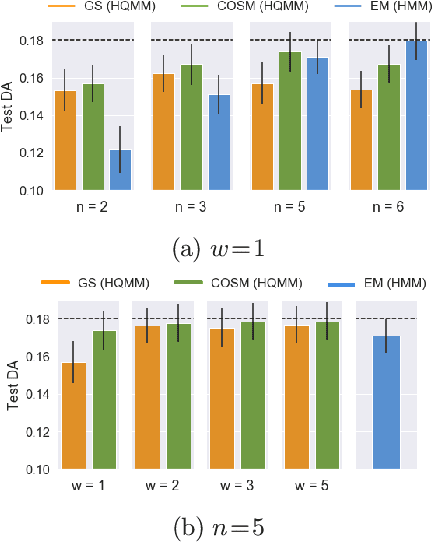
Extending classical probabilistic reasoning using the quantum mechanical view of probability has been of recent interest, particularly in the development of hidden quantum Markov models (HQMMs) to model stochastic processes. However, there has been little progress in characterizing the expressiveness of such models and learning them from data. We tackle these problems by showing that HQMMs are a special subclass of the general class of observable operator models (OOMs) that do not suffer from the \emph{negative probability problem} by design. We also provide a feasible retraction-based learning algorithm for HQMMs using constrained gradient descent on the Stiefel manifold of model parameters. We demonstrate that this approach is faster and scales to larger models than previous learning algorithms.

Learning Quantum Graphical Models using Constrained Gradient Descent on the Stiefel Manifold

Quantum graphical models (QGMs) extend the classical framework for reasoning about uncertainty by incorporating the quantum mechanical view of probability. Prior work on QGMs has focused on hidden quantum Markov models (HQMMs), which can be formulated using quantum analogues of the sum rule and Bayes rule used in classical graphical models. Despite the focus on developing the QGM framework, there has been little progress in learning these models from data. The existing state-of-the-art approach randomly initializes parameters and iteratively finds unitary transformations that increase the likelihood of the data. While this algorithm demonstrated theoretical strengths of HQMMs over HMMs, it is slow and can only handle a small number of hidden states. In this paper, we tackle the learning problem by solving a constrained optimization problem on the Stiefel manifold using a well-known retraction-based algorithm. We demonstrate that this approach is not only faster and yields better solutions on several datasets, but also scales to larger models that were prohibitively slow to train via the earlier method.