Auctions and Prediction Markets for Scientific Peer Review

Peer reviewed publications are considered the gold standard in certifying and disseminating ideas that a research community considers valuable. However, we identify two major drawbacks of the current system: (1) the overwhelming demand for reviewers due to a large volume of submissions, and (2) the lack of incentives for reviewers to participate and expend the necessary effort to provide high-quality reviews. In this work, we adopt a mechanism-design approach to propose improvements to the peer review process. We present a two-stage mechanism which ties together the paper submission and review process, simultaneously incentivizing high-quality reviews and high-quality submissions. In the first stage, authors participate in a VCG auction for review slots by submitting their papers along with a bid that represents their expected value for having their paper reviewed. For the second stage, we propose a novel prediction market-style mechanism (H-DIPP) building on recent work in the information elicitation literature, which incentivizes participating reviewers to provide honest and effortful reviews. The revenue raised by the Stage I auction is used in Stage II to pay reviewers based on the quality of their reviews.

Learning Deep Features in Instrumental Variable Regression

Instrumental variable (IV) regression is a standard strategy for learning causal relationships between confounded treatment and outcome variables from observational data by utilizing an instrumental variable, which affects the outcome only through the treatment. In classical IV regression, learning proceeds in two stages: stage 1 performs linear regression from the instrument to the treatment; and stage 2 performs linear regression from the treatment to the outcome, conditioned on the instrument. We propose a novel method, deep feature instrumental variable regression (DFIV), to address the case where relations between instruments, treatments, and outcomes may be nonlinear. In this case, deep neural nets are trained to define informative nonlinear features on the instruments and treatments. We propose an alternating training regime for these features to ensure good end-to-end performance when composing stages 1 and 2, thus obtaining highly flexible feature maps in a computationally efficient manner. DFIV outperforms recent state-of-the-art methods on challenging IV benchmarks, including settings involving high dimensional image data. DFIV also exhibits competitive performance in off-policy policy evaluation for reinforcement learning, which can be understood as an IV regression task.

Quantum Tensor Networks, Stochastic Processes, and Weighted Automata

Modeling joint probability distributions over sequences has been studied from many perspectives. The physics community developed matrix product states, a tensor-train decomposition for probabilistic modeling, motivated by the need to tractably model many-body systems. But similar models have also been studied in the stochastic processes and weighted automata literature, with little work on how these bodies of work relate to each other. We address this gap by showing how stationary or uniform versions of popular quantum tensor network models have equivalent representations in the stochastic processes and weighted automata literature, in the limit of infinitely long sequences. We demonstrate several equivalence results between models used in these three communities: (i) uniform variants of matrix product states, Born machines and locally purified states from the quantum tensor networks literature, (ii) predictive state representations, hidden Markov models, norm-observable operator models and hidden quantum Markov models from the stochastic process literature,and (iii) stochastic weighted automata, probabilistic automata and quadratic automata from the formal languages literature. Such connections may open the door for results and methods developed in one area to be applied in another.

Expressiveness and Learning of Hidden Quantum Markov Models

Extending classical probabilistic reasoning using the quantum mechanical view of probability has been of recent interest, particularly in the development of hidden quantum Markov models (HQMMs) to model stochastic processes. However, there has been little progress in characterizing the expressiveness of such models and learning them from data. We tackle these problems by showing that HQMMs are a special subclass of the general class of observable operator models (OOMs) that do not suffer from the \emph{negative probability problem} by design. We also provide a feasible retraction-based learning algorithm for HQMMs using constrained gradient descent on the Stiefel manifold of model parameters. We demonstrate that this approach is faster and scales to larger models than previous learning algorithms.

Learning Quantum Graphical Models using Constrained Gradient Descent on the Stiefel Manifold

Quantum graphical models (QGMs) extend the classical framework for reasoning about uncertainty by incorporating the quantum mechanical view of probability. Prior work on QGMs has focused on hidden quantum Markov models (HQMMs), which can be formulated using quantum analogues of the sum rule and Bayes rule used in classical graphical models. Despite the focus on developing the QGM framework, there has been little progress in learning these models from data. The existing state-of-the-art approach randomly initializes parameters and iteratively finds unitary transformations that increase the likelihood of the data. While this algorithm demonstrated theoretical strengths of HQMMs over HMMs, it is slow and can only handle a small number of hidden states. In this paper, we tackle the learning problem by solving a constrained optimization problem on the Stiefel manifold using a well-known retraction-based algorithm. We demonstrate that this approach is not only faster and yields better solutions on several datasets, but also scales to larger models that were prohibitively slow to train via the earlier method.

Learning and Inference in Hilbert Space with Quantum Graphical Models

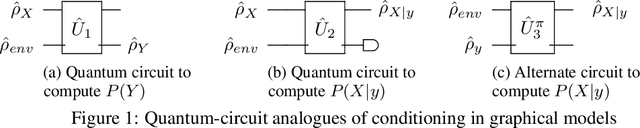
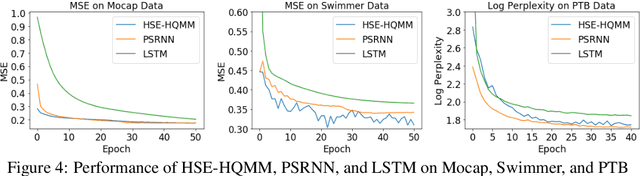
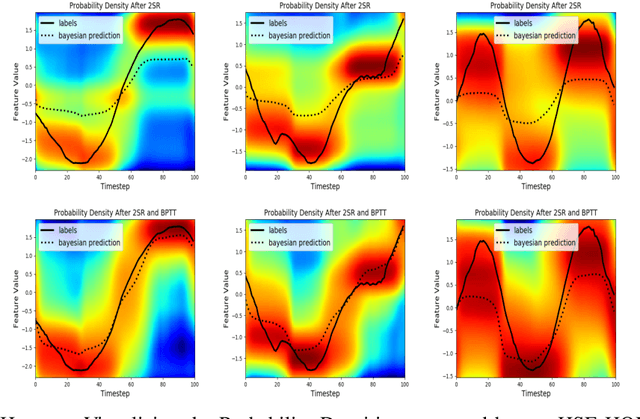
Quantum Graphical Models (QGMs) generalize classical graphical models by adopting the formalism for reasoning about uncertainty from quantum mechanics. Unlike classical graphical models, QGMs represent uncertainty with density matrices in complex Hilbert spaces. Hilbert space embeddings (HSEs) also generalize Bayesian inference in Hilbert spaces. We investigate the link between QGMs and HSEs and show that the sum rule and Bayes rule for QGMs are equivalent to the kernel sum rule in HSEs and a special case of Nadaraya-Watson kernel regression, respectively. We show that these operations can be kernelized, and use these insights to propose a Hilbert Space Embedding of Hidden Quantum Markov Models (HSE-HQMM) to model dynamics. We present experimental results showing that HSE-HQMMs are competitive with state-of-the-art models like LSTMs and PSRNNs on several datasets, while also providing a nonparametric method for maintaining a probability distribution over continuous-valued features.

A Simple and Effective Approach to the Story Cloze Test

In the Story Cloze Test, a system is presented with a 4-sentence prompt to a story, and must determine which one of two potential endings is the 'right' ending to the story. Previous work has shown that ignoring the training set and training a model on the validation set can achieve high accuracy on this task due to stylistic differences between the story endings in the training set and validation and test sets. Following this approach, we present a simpler fully-neural approach to the Story Cloze Test using skip-thought embeddings of the stories in a feed-forward network that achieves close to state-of-the-art performance on this task without any feature engineering. We also find that considering just the last sentence of the prompt instead of the whole prompt yields higher accuracy with our approach.

Learning Hidden Quantum Markov Models

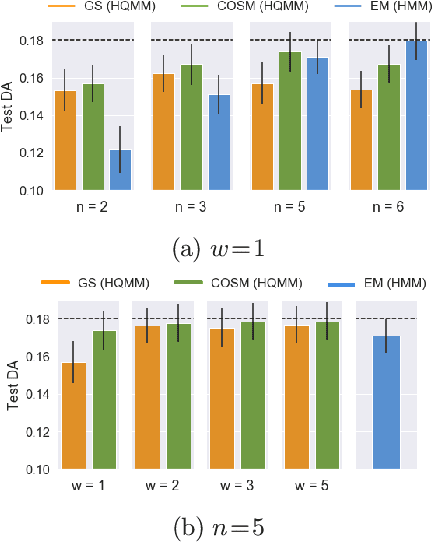
Hidden Quantum Markov Models (HQMMs) can be thought of as quantum probabilistic graphical models that can model sequential data. We extend previous work on HQMMs with three contributions: (1) we show how classical hidden Markov models (HMMs) can be simulated on a quantum circuit, (2) we reformulate HQMMs by relaxing the constraints for modeling HMMs on quantum circuits, and (3) we present a learning algorithm to estimate the parameters of an HQMM from data. While our algorithm requires further optimization to handle larger datasets, we are able to evaluate our algorithm using several synthetic datasets. We show that on HQMM generated data, our algorithm learns HQMMs with the same number of hidden states and predictive accuracy as the true HQMMs, while HMMs learned with the Baum-Welch algorithm require more states to match the predictive accuracy.