Training-efficient density quantum machine learning

Quantum machine learning requires powerful, flexible and efficiently trainable models to be successful in solving challenging problems. In this work, we present density quantum neural networks, a learning model incorporating randomisation over a set of trainable unitaries. These models generalise quantum neural networks using parameterised quantum circuits, and allow a trade-off between expressibility and efficient trainability, particularly on quantum hardware. We demonstrate the flexibility of the formalism by applying it to two recently proposed model families. The first are commuting-block quantum neural networks (QNNs) which are efficiently trainable but may be limited in expressibility. The second are orthogonal (Hamming-weight preserving) quantum neural networks which provide well-defined and interpretable transformations on data but are challenging to train at scale on quantum devices. Density commuting QNNs improve capacity with minimal gradient complexity overhead, and density orthogonal neural networks admit a quadratic-to-constant gradient query advantage with minimal to no performance loss. We conduct numerical experiments on synthetic translationally invariant data and MNIST image data with hyperparameter optimisation to support our findings. Finally, we discuss the connection to post-variational quantum neural networks, measurement-based quantum machine learning and the dropout mechanism.

Quantum Deep Hedging

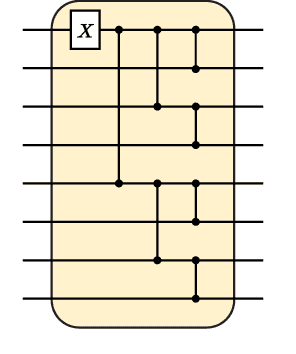
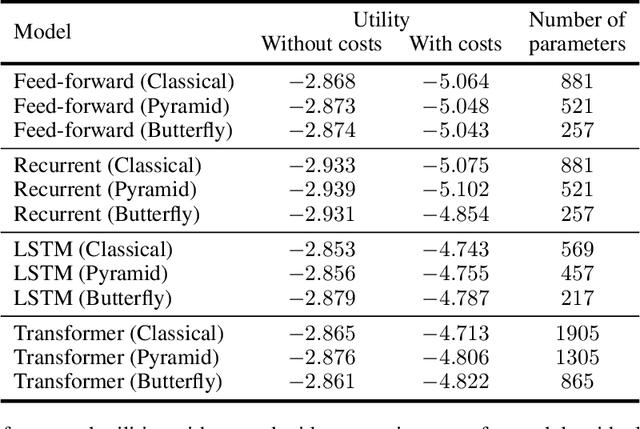
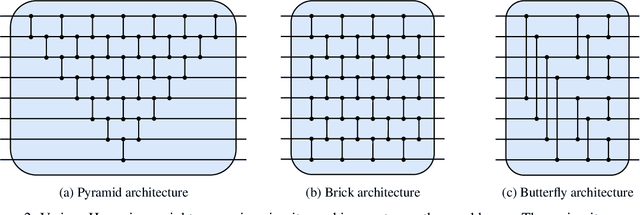
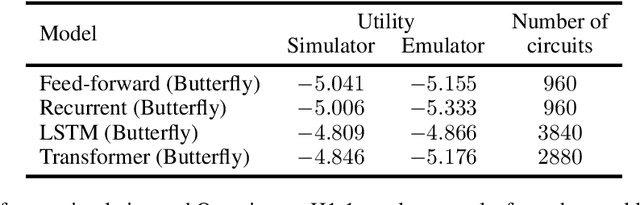
Quantum machine learning has the potential for a transformative impact across industry sectors and in particular in finance. In our work we look at the problem of hedging where deep reinforcement learning offers a powerful framework for real markets. We develop quantum reinforcement learning methods based on policy-search and distributional actor-critic algorithms that use quantum neural network architectures with orthogonal and compound layers for the policy and value functions. We prove that the quantum neural networks we use are trainable, and we perform extensive simulations that show that quantum models can reduce the number of trainable parameters while achieving comparable performance and that the distributional approach obtains better performance than other standard approaches, both classical and quantum. We successfully implement the proposed models on a trapped-ion quantum processor, utilizing circuits with up to $16$ qubits, and observe performance that agrees well with noiseless simulation. Our quantum techniques are general and can be applied to other reinforcement learning problems beyond hedging.

Quantum Vision Transformers

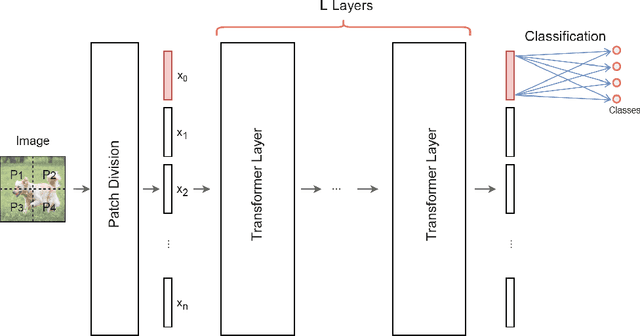
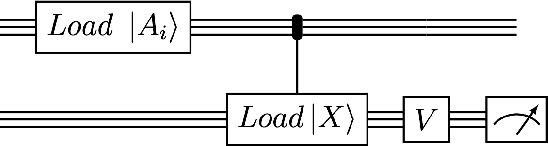
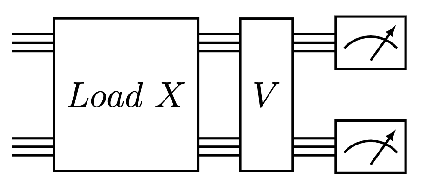
We design and analyse quantum transformers, extending the state-of-the-art classical transformer neural network architectures known to be very performant in natural language processing and image analysis. Building upon the previous work of parametrised quantum circuits for data loading and orthogonal neural layers, we introduce three quantum attention mechanisms, including a quantum transformer based on compound matrices. These quantum architectures can be built using shallow quantum circuits and can provide qualitatively different classification models. We performed extensive simulations of the quantum transformers on standard medical image datasets that showed competitive, and at times better, performance compared with the best classical transformers and other classical benchmarks. The computational complexity of our quantum attention layer proves to be advantageous compared with the classical algorithm with respect to the size of the classified images. Our quantum architectures have thousands of parameters compared with the best classical methods with millions of parameters. Finally, we have implemented our quantum transformers on superconducting quantum computers and obtained encouraging results for up to six qubit experiments.

Quantum Reinforcement Learning via Policy Iteration

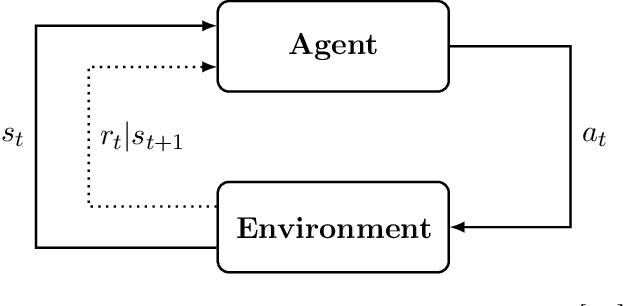
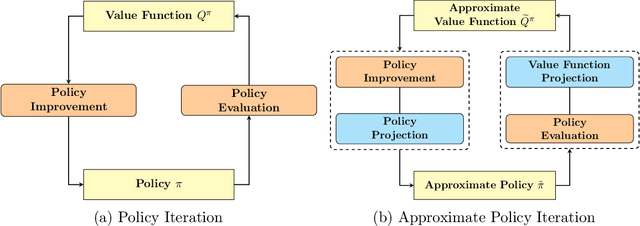
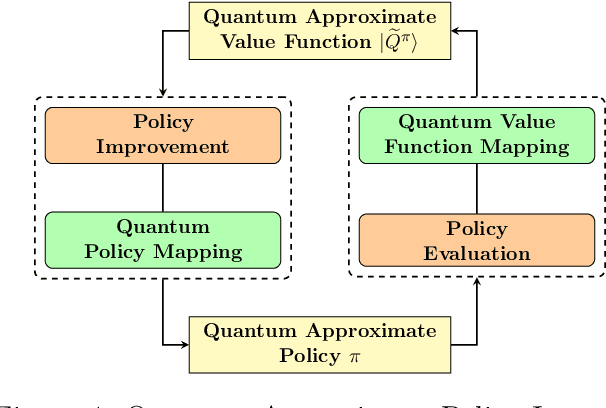
Quantum computing has shown the potential to substantially speed up machine learning applications, in particular for supervised and unsupervised learning. Reinforcement learning, on the other hand, has become essential for solving many decision making problems and policy iteration methods remain the foundation of such approaches. In this paper, we provide a general framework for performing quantum reinforcement learning via policy iteration. We validate our framework by designing and analyzing: \emph{quantum policy evaluation} methods for infinite horizon discounted problems by building quantum states that approximately encode the value function of a policy $\pi$; and \emph{quantum policy improvement} methods by post-processing measurement outcomes on these quantum states. Last, we study the theoretical and experimental performance of our quantum algorithms on two environments from OpenAI's Gym.

Quantum algorithms for Second-Order Cone Programming and Support Vector Machines

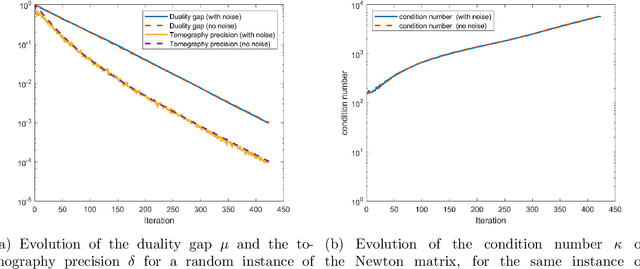
Second order cone programs (SOCPs) are a class of structured convex optimization problems that generalize linear programs. We present a quantum algorithm for SOCPs based on a quantum variant of the interior point method. Our algorithm outputs a classical solution to the SOCP with objective value $\epsilon$ close to the optimal in time $\widetilde{O} \left( n\sqrt{r} \frac{\zeta \kappa}{\delta^2} \log \left(1/\epsilon\right) \right)$ where $r$ is the rank and $n$ the dimension of the SOCP, $\delta$ bounds the distance from strict feasibility for the intermediate solutions, $\zeta$ is a parameter bounded by $\sqrt{n}$, and $\kappa$ is an upper bound on the condition number of matrices arising in the classical interior point method for SOCPs. We present applications to the support vector machine (SVM) problem in machine learning that reduces to SOCPs. We provide experimental evidence that the quantum algorithm achieves an asymptotic speedup over classical SVM algorithms with a running time $\widetilde{O}(n^{2.557})$ for random SVM instances. The best known classical algorithms for such instances have complexity $\widetilde{O} \left( n^{\omega+0.5}\log(1/\epsilon) \right)$, where $\omega$ is the matrix multiplication exponent that has a theoretical value of around $2.373$, but is closer to $3$ in practice.

Quantum Expectation-Maximization for Gaussian Mixture Models

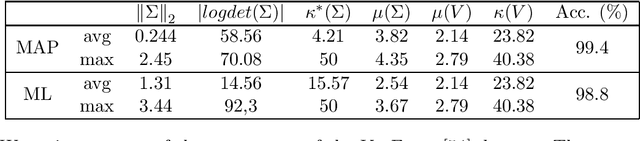
The Expectation-Maximization (EM) algorithm is a fundamental tool in unsupervised machine learning. It is often used as an efficient way to solve Maximum Likelihood (ML) estimation problems, especially for models with latent variables. It is also the algorithm of choice to fit mixture models: generative models that represent unlabelled points originating from $k$ different processes, as samples from $k$ multivariate distributions. In this work we define and use a quantum version of EM to fit a Gaussian Mixture Model. Given quantum access to a dataset of $n$ vectors of dimension $d$, our algorithm has convergence and precision guarantees similar to the classical algorithm, but the runtime is only polylogarithmic in the number of elements in the training set, and is polynomial in other parameters - as the dimension of the feature space, and the number of components in the mixture. We generalize further the algorithm in two directions. First, we show how to fit any mixture model of probability distributions in the exponential family. Then, we show how to use this algorithm to compute the Maximum a Posteriori (MAP) estimate of a mixture model: the Bayesian approach to likelihood estimation problems. We discuss the performance of the algorithm on datasets that are expected to be classified successfully by those algorithms, arguing that on those cases we can give strong guarantees on the runtime.

q-means: A quantum algorithm for unsupervised machine learning

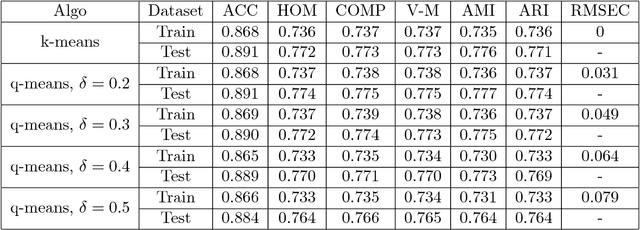
Quantum machine learning is one of the most promising applications of a full-scale quantum computer. Over the past few years, many quantum machine learning algorithms have been proposed that can potentially offer considerable speedups over the corresponding classical algorithms. In this paper, we introduce q-means, a new quantum algorithm for clustering which is a canonical problem in unsupervised machine learning. The $q$-means algorithm has convergence and precision guarantees similar to $k$-means, and it outputs with high probability a good approximation of the $k$ cluster centroids like the classical algorithm. Given a dataset of $N$ $d$-dimensional vectors $v_i$ (seen as a matrix $V \in \mathbb{R}^{N \times d})$ stored in QRAM, the running time of q-means is $\widetilde{O}\left( k d \frac{\eta}{\delta^2}\kappa(V)(\mu(V) + k \frac{\eta}{\delta}) + k^2 \frac{\eta^{1.5}}{\delta^2} \kappa(V)\mu(V) \right)$ per iteration, where $\kappa(V)$ is the condition number, $\mu(V)$ is a parameter that appears in quantum linear algebra procedures and $\eta = \max_{i} ||v_{i}||^{2}$. For a natural notion of well-clusterable datasets, the running time becomes $\widetilde{O}\left( k^2 d \frac{\eta^{2.5}}{\delta^3} + k^{2.5} \frac{\eta^2}{\delta^3} \right)$ per iteration, which is linear in the number of features $d$, and polynomial in the rank $k$, the maximum square norm $\eta$ and the error parameter $\delta$. Both running times are only polylogarithmic in the number of datapoints $N$. Our algorithm provides substantial savings compared to the classical $k$-means algorithm that runs in time $O(kdN)$ per iteration, particularly for the case of large datasets.

Quantum algorithms for feedforward neural networks

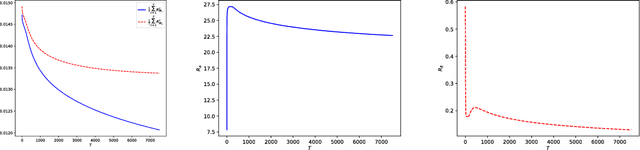
Quantum machine learning has the potential for broad industrial applications, and the development of quantum algorithms for improving the performance of neural networks is of particular interest given the central role they play in machine learning today. In this paper we present quantum algorithms for training and evaluating feedforward neural networks based on the canonical classical feedforward and backpropagation algorithms. Our algorithms rely on an efficient quantum subroutine for approximating the inner products between vectors, and on storing intermediate values in quantum random access memory for fast retrieval at later stages. The running times of our algorithms can be quadratically faster than their classical counterparts, since they depend linearly on the number of neurons in the network, as opposed to the number of edges as in the classical case. This makes our algorithms suited for large-scale, highly-connected networks where the number of edges in the network dominates the classical algorithmic running time.

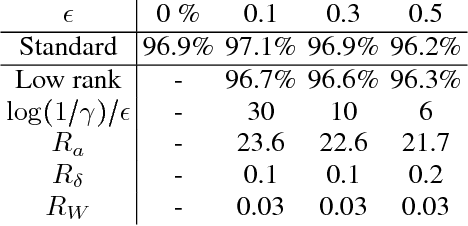
Quantum classification of the MNIST dataset via Slow Feature Analysis

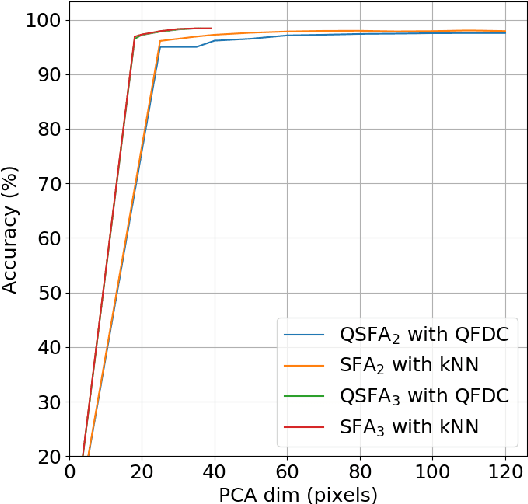
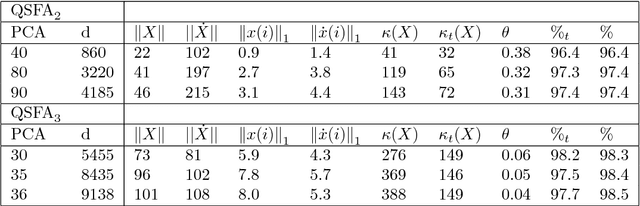
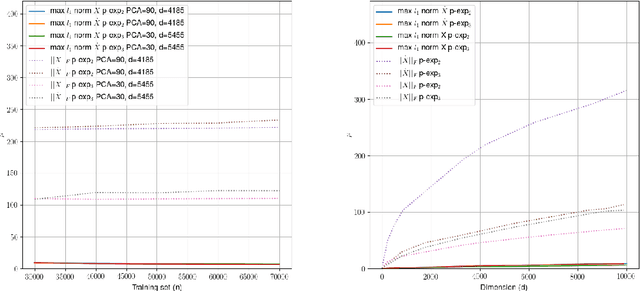
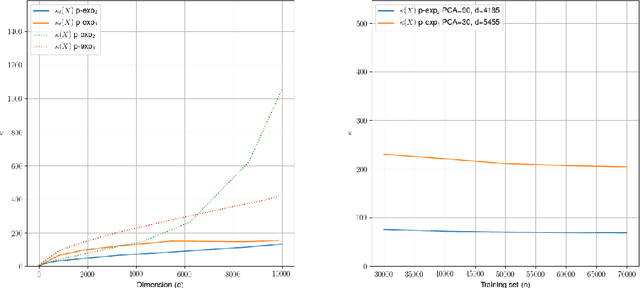
Quantum machine learning carries the promise to revolutionize information and communication technologies. While a number of quantum algorithms with potential exponential speedups have been proposed already, it is quite difficult to provide convincing evidence that quantum computers with quantum memories will be in fact useful to solve real-world problems. Our work makes considerable progress towards this goal. We design quantum techniques for Dimensionality Reduction and for Classification, and combine them to provide an efficient and high accuracy quantum classifier that we test on the MNIST dataset. More precisely, we propose a quantum version of Slow Feature Analysis (QSFA), a dimensionality reduction technique that maps the dataset in a lower dimensional space where we can apply a novel quantum classification procedure, the Quantum Frobenius Distance (QFD). We simulate the quantum classifier (including errors) and show that it can provide classification of the MNIST handwritten digit dataset, a widely used dataset for benchmarking classification algorithms, with $98.5\%$ accuracy, similar to the classical case. The running time of the quantum classifier is polylogarithmic in the dimension and number of data points. We also provide evidence that the other parameters on which the running time depends (condition number, Frobenius norm, error threshold, etc.) scale favorably in practice, thus ascertaining the efficiency of our algorithm.